Capítulo 38 – O Efeito da Taxa de Aprendizagem no Treinamento de Redes Neurais Artificiais
Vamos retomar a discussão do capítulo anterior e tentar melhorar a precisão do modelo nos dados de teste a partir de um tamanho de lote maior, aumentando a taxa de aprendizado (learning rate). Vamos estudar O Efeito da Taxa de Aprendizagem no Treinamento de Redes Neurais Artificiais.
Algumas pesquisas na literatura sobre otimização em Machine Learning mostraram que aumentar a taxa de aprendizado pode compensar tamanhos maiores de lotes. Com isso em mente, aumentamos a taxa de aprendizado do nosso modelo para ver se podemos recuperar a precisão nos dados de teste (que havia sido reduzida quando aumentando o tamanho do lote). Os gráficos abaixo mostram as conclusões:
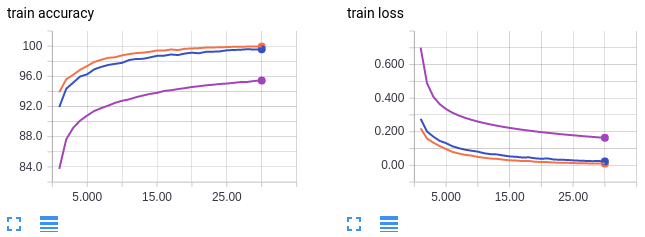
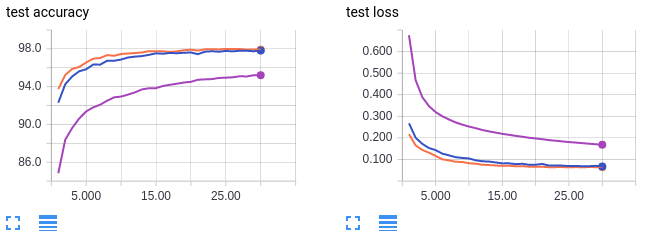
Curvas em laranja: tamanho do lote 64, taxa de aprendizagem 0.01 (referência)
Curvas em lilás: tamanho do lote 1024, taxa de aprendizado de 0,01 (referência)
Curvas em azul: tamanho do lote 1024, taxa de aprendizagem 0,1
As curvas em laranja e lilás são para referência e são as mesmas do conjunto de gráficos do capítulo anterior. Como a curva lilás, a curva azul treina com um tamanho de lote grande de 1024. No entanto, a curva azul tem uma taxa de aprendizado aumentada em 10 vezes. Curiosamente, podemos recuperar a precisão nos dados de teste a partir de um tamanho de lote maior, aumentando a taxa de aprendizado. Usando um tamanho de lote de 64 (laranja) atinge uma precisão de teste de 98%, enquanto o uso de um tamanho de lote de 1024 atinge apenas cerca de 96%. Mas aumentando a taxa de aprendizado, usando um tamanho de lote de 1024 também alcança uma precisão de teste de 98%. Assim como com nossa conclusão anterior, tenha cautela ao analisar esses resultados. Sabe-se que o simples aumento da taxa de aprendizado não compensa totalmente grandes tamanhos de lotes em conjuntos de dados mais complexos do que o MNIST.
E qual o efeito ao reduzir o tamanho do lote durante o treinamento do modelo?
A próxima pergunta interessante a ser feita é se o treinamento com lotes grandes “inicia você em um caminho ruim do qual você não pode se recuperar”. Ou seja, se começarmos a treinar com tamanho de lote 1024, então mudamos para tamanho de lote 64, podemos ainda alcançar a maior precisão em teste de 98%?
Investigamos três casos: treinar usando um tamanho de lote pequeno para uma única época, mudar para um tamanho de lote grande, treinar usando um tamanho de lote pequeno para muitas épocas e mudar para um tamanho maior de lote e treinar usando um tamanho grande de lote e então usar uma taxa de aprendizado mais alta com o mesmo tamanho de lote. Resultados abaixo:
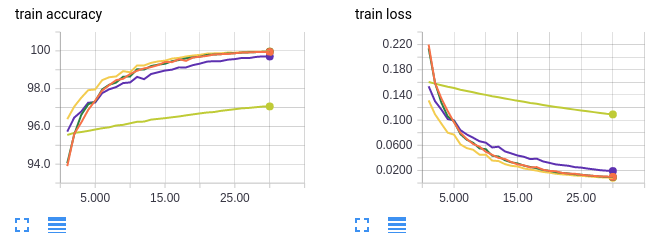
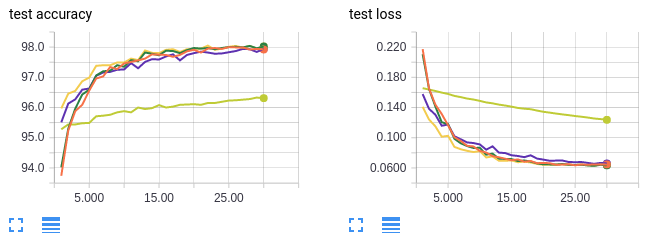
- Curvas em laranja: treinar em tamanho de lote 64 por 30 épocas (referência).
- Curvas em amarelo neon: treinar em tamanho de lote 1024 por 60 épocas (referência).
- Curvas em verde: treinar em tamanho de lote 1024 para 1 época e depois mudar para tamanho de lote 64 por 30 épocas (total de 31 épocas).
- Curvas em amarelo escuro: treinar em tamanho de lote 1024 por 30 épocas e depois mudar para tamanho de lote 64 por 30 épocas (total de 60 épocas).
- Curvas em lilás: treinamento em tamanho de lote 1024 e aumento da taxa de aprendizado em 10x na época 31 (total de 60 épocas).
Como antes, as curvas em laranja são para um tamanho de lote pequeno. As curvas em amarelo neon servem como um controle para garantir que não estamos melhorando a precisão do teste porque estamos simplesmente treinando mais. Se você prestar muita atenção ao eixo x, as épocas são enumeradas de 0 a 30. Isso ocorre porque somente as últimas 30 épocas de treinamento são mostradas. Para experimentos com mais de 30 épocas de treinamento no total, as primeiras x – 30 épocas foram omitidas.
É difícil ver as outras 3 linhas porque elas estão sobrepostas, mas não importa, porque nos três casos recuperamos a precisão em teste de 98%! Em conclusão, começar com um tamanho grande de lote não “pega o modelo preso” em alguma vizinhança de ótimos locais ideais. O modelo pode alternar para um tamanho de lote menor ou uma taxa de aprendizado mais alta a qualquer momento para obter uma precisão de teste melhor.
Para compreender o comportamento matemático por trás de todo esse processo, precisamos trazer o gradiente para esta discussão. É o que faremos no próximo capítulo. Até lá.
Referências:
Don’t Decay the Learning Rate, Increase the Batch Size
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Effect of batch size on training dynamics
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

