Capítulo 65 – Distribuições de Probabilidade, Redes Neurais e Reinforcement Learning

Nos capítulos anteriores estudamos os conceitos gerais ligados ao Aprendizado Por Reforço (Reinforcement Learning). A partir de agora vamos entrar nos detalhes mais técnicos ligados a este importante método de aprendizagem de máquina, estudando Distribuições de Probabilidade, Redes Neurais e Reinforcement Learning. Acompanhe.

O Objetivo do Aprendizado Por Reforço

O objetivo do Aprendizado Por Reforço é escolher a melhor ação para qualquer estado, o que significa que as ações devem ser classificadas e valores devem ser atribuídos em relação uma a outra. Como essas ações dependem do estado, o que realmente estamos medindo é o valor dos pares de ação e estado; ou seja, uma ação tomada de um determinado estado, algo que o agente fez em algum lugar. Aqui estão alguns exemplos para demonstrar que o valor e o significado de uma ação dependem do estado em que é tomada:

Se a ação é se casar com alguém, casar com uma pessoa de 35 anos quando você tem 18 anos provavelmente significa algo diferente de casar com uma pessoa de 35 anos quando você tem 90 anos, e esses dois resultados provavelmente têm motivações diferentes e levam a diferentes resultados.
Se a ação estiver gritando “Fogo!”, Então executar a ação em um teatro lotado deve significar algo diferente de executar a ação ao lado de um esquadrão de homens armados com metralhadoras. Não podemos prever o resultado de uma ação sem conhecer o contexto.

Mapeamos os pares estado-ação para os valores que esperamos que eles produzam com a função Q, descrita no capítulo anterior. A função Q usa como entrada o estado e a ação de um agente e os mapeia para prováveis recompensas.

O Aprendizado Por Reforço é o processo de executar o agente por meio de sequências de pares de ação e estado, observando as recompensas resultantes e adaptando as previsões da função Q àquelas recompensas até que ele preveja com precisão o melhor caminho a ser seguido pelo agente. Essa previsão é conhecida como uma política.

Distribuição de Probabilidade

O Aprendizado Por Reforço é uma tentativa de modelar uma distribuição de probabilidade complexa de recompensas em relação a um número muito grande de pares de ação de estado. Esse é um dos motivos pelos quais o Aprendizado Por Reforço é combinado com, digamos, um processo de decisão de Markov, um método de amostragem de uma distribuição complexa para inferir suas propriedades. Assemelha-se muito ao problema que inspirou Stan Ulam a inventar o método de Monte Carlo; ou seja, tentar inferir as chances de que uma determinada “mão” em um jogo de carta seja bem-sucedida.

Qualquer abordagem estatística é essencialmente uma confissão de ignorância. A imensa complexidade de alguns fenômenos (biológicos, políticos, sociológicos ou relacionados a jogos de tabuleiro) torna impossível raciocinar a partir de alguns princípios. A única maneira de estudá-los é através da estatística, medindo eventos superficiais e tentando estabelecer correlações entre eles, mesmo quando não entendemos o mecanismo pelo qual eles se relacionam. O Aprendizado Por Reforço, como redes neurais profundas, é uma dessas estratégias, contando com a amostragem para extrair informações dos dados.

Depois de um pouco de tempo empregando algo como um processo de decisão de Markov para aproximar a distribuição de probabilidade da recompensa sobre pares de ação do estado, um algoritmo de Aprendizado Por Reforço pode tender a repetir ações que levam à recompensa e deixar de testar alternativas. Há uma tensão entre a exploração de recompensas conhecidas e a exploração contínua para descobrir novas ações que também levam à vitória. Assim como as empresas de petróleo têm a dupla função de extrair petróleo de campos conhecidos e perfurar novas reservas, também podem ser criados algoritmos de Aprendizado Por Reforço para explorar em graus variados, a fim de garantir que eles não tomem ações recompensadoras em detrimento de vencedores conhecidos.

O Aprendizado Por Reforço é iterativo. Em suas aplicações mais interessantes, não começa sabendo quais recompensas os pares de ação e estado produzirão. Ele aprende essas relações percorrendo estados repetidas vezes, como atletas ou músicos percorrem estados na tentativa de melhorar seu desempenho.

Redes Neurais

E onde as redes neurais se encaixam?

As redes neurais são aproximadores de função, que são particularmente úteis no Aprendizado Por Reforço quando o espaço de estado ou espaço de ação é muito grande para ser completamente conhecido.

Uma rede neural pode ser usada para aproximar uma função de valor ou uma função de política. Ou seja, as redes neurais podem aprender a mapear estados para valores ou pares de ação e estado para valores Q. Em vez de usar uma tabela de pesquisa para armazenar, indexar e atualizar todos os estados possíveis e seus valores, o que é impossível com problemas muito grandes, podemos treinar uma rede neural em amostras do estado ou espaço de ação para aprender a prever o quanto esses valores são importantes, nosso objetivo no Aprendizado Por Reforço.

As redes neurais usam coeficientes para aproximar a função que relaciona insumos (entradas) a produtos (saídas), e seu aprendizado consiste em encontrar os coeficientes ou pesos certos, ajustando iterativamente esses pesos ao longo de gradientes que prometem menos erros. No Aprendizado Por Reforço, redes convolucionais podem ser usadas para reconhecer o estado de um agente quando a entrada é visual; por exemplo. a tela em que o agente está em um jogo, ou o terreno percorrido por um drone. Ou seja, eles realizam sua tarefa típica de reconhecimento de imagem.

Mas as redes convolucionais derivam interpretações diferentes das imagens no Aprendizado Por Reforço do que no Aprendizado Supervisionado. No Aprendizado Supervisionado, a rede aplica um rótulo a uma imagem, como no exemplo abaixo:

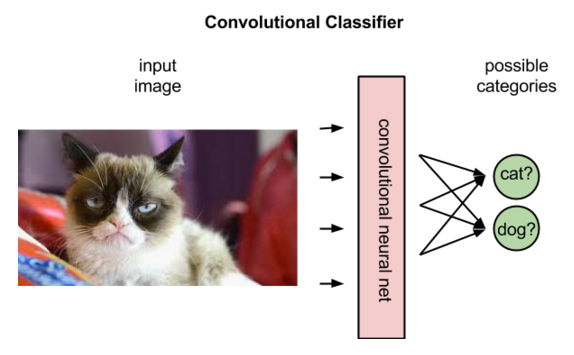
De fato, a rede classificará os rótulos que melhor se ajustam à imagem em termos de probabilidades. Na imagem de um gato, pode-se decidir que a imagem tem 80% de probabilidade de ser um gato, 50% de ser um cavalo e 30% de ser um cachorro.

No Aprendizado Por Reforço, dada uma imagem que representa um estado, uma rede convolucional pode classificar as ações possíveis de executar nesse estado; por exemplo, pode prever que correr à direita retornará 5 pontos, pular 7 e correr à esquerda nenhum.

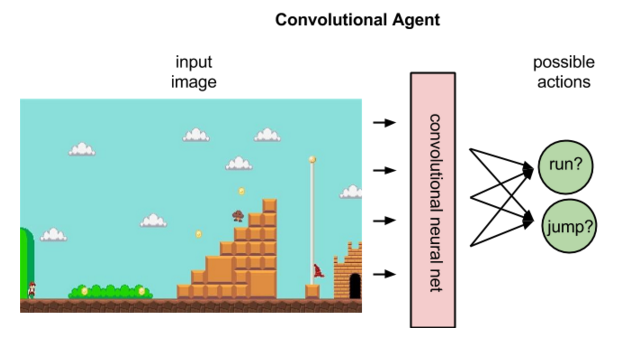
A imagem acima ilustra o que um agente faz, mapeando um estado para a melhor ação.

Reinforcement Learning

Uma política mapeia um estado para uma ação.

Se você se lembra, isso é diferente de Q, que mapeia pares de ações de estado para recompensas.

Para ser mais específico, Q mapeia pares de ação de estado para a combinação mais alta de recompensa imediata com todas as recompensas futuras que podem ser obtidas por ações posteriores na trajetória. Aqui está a equação para Q:

Depois de atribuir valores às recompensas esperadas, a função Q simplesmente seleciona o par de ação de estado com o maior valor chamado Q.

No início do Aprendizado Por Reforço, os coeficientes da rede neural podem ser inicializados estocástica ou aleatoriamente. Usando o feedback do ambiente, a rede neural pode usar a diferença entre sua recompensa esperada e a recompensa verdadeira para ajustar seus pesos e melhorar sua interpretação dos pares de ação do estado.

Esse ciclo de feedback é análogo à retropropagação de erro no Aprendizado Supervisionado. No entanto, o Aprendizado Supervisionado começa com o conhecimento dos rótulos verdadeiros que a rede neural está tentando prever. Seu objetivo é criar um modelo que mapeie imagens diferentes para seus respectivos nomes.

O Aprendizado Por Reforço depende do ambiente para enviar a ele um número escalar em resposta a cada nova ação. As recompensas retornadas pelo ambiente podem ser variadas, atrasadas ou afetadas por variáveis desconhecidas, introduzindo ruído no loop de feedback. Isso nos leva a uma expressão mais completa da função Q, que leva em consideração não apenas as recompensas imediatas produzidas por uma ação, mas também as recompensas atrasadas que podem ser retornadas várias vezes mais fundo na sequência.

Como seres humanos, a função Q é recursiva. Chamar a função Q em um determinado par de estado-ação exige que chamemos uma função Q aninhada para prever o valor do próximo estado, que por sua vez depende da função Q do estado seguinte e assim por diante.

Continue acompanhando os próximos capítulos.

Referências:

Inteligência Artificial Aplicada a Finanças

Customizando Redes Neurais com Funções de Ativação Alternativas

A Beginner’s Guide to Deep Reinforcement Learning

What is reinforcement learning? The complete guide

Reinforcement learning

Applications of Reinforcement Learning in Real World

Practical Recommendations for Gradient-Based Training of Deep Architectures

Gradient-Based Learning Applied to Document Recognition

Neural Networks & The Backpropagation Algorithm, Explained

Recurrent neural network based language model