Capítulo 66 – Algoritmo de Agente Baseado em IA com Reinforcement Learning – Parte 1

O Aprendizado por Reforço (Reinforcement Learning) é uma abordagem computacional para entender e automatizar aprendizado direcionado e tomada de decisão. Distingue-se de outras abordagens por sua ênfase na aprendizagem de um agente a partir da interação direta com seu ambiente, sem exigir supervisão ou modelos completos do ambiente.

Em nossa opinião, a Aprendizado por Reforço é o primeiro campo a abordar seriamente problemas computacionais que surgem ao aprender com a interação com um ambiente para atingir objetivos de longo prazo. É um dos métodos mais avançados em Inteligência Artificial.

O Aprendizado por Reforço usa a estrutura formal dos Processos de Decisão de Markov para definir a interação entre um agente de aprendizagem e seu ambiente em termos de estados, ações e recompensas. Essa estrutura pretende ser uma maneira simples de representar características essenciais do problema de Inteligência Artificial. Esses recursos incluem uma sensação de causa e efeito, um senso de incerteza e não-determinismo, e a existência de metas explícitas. Algo muito similar ao aprendizado humano.

Os conceitos de valor e função de valor são essenciais para a maior parte dos métodos de Aprendizado por Reforço. Assumimos a posição de que a função de valor é importante para a pesquisa eficiente no espaço das políticas. O uso de funções de valor distingue os métodos de Aprendizado por Reforço dos métodos evolutivos que buscam diretamente no espaço de políticas orientado por avaliações de políticas inteiras.

Para ilustrar a ideia geral do Aprendizado por Reforço, vamos descrever um algoritmo (conjunto de etapas) que implementa o que seria um agente baseado em IA usando essa técnica. Passaremos por cada detalhe do algoritmo, inclusive alguns detalhes matemáticos. A construção de um algoritmo é a primeira parte do trabalho de construção de uma aplicação de Inteligência Artificial. Vamos usar o contexto de um jogo, para que o exemplo fique ainda mais claro. Mas o processo descrito aqui não é muito diferente de um agente de carro autônomo, por exemplo.

Muitos se preocupam apenas com a programação, sem compreender que existe um raciocínio lógico antes disso, que determina como deve ser a solução a ser implementada. Esse raciocínio lógico pode ser descrito em etapas, o que chamados de algoritmo. Isso é o que queremos praticar com você agora.

Algoritmo de um Agente Baseado em IA

Considere o famoso Jogo da Velha.

Dois jogadores revezam-se jogando em um tabuleiro de três por três, conforme a figura acima. Um jogador joga Xs e o outro OS até que um jogador ganhe colocando três marcas em uma fileira, horizontal, vertical ou diagonal. Se o tabuleiro estiver totalmente preenchido e nenhum jogador conseguir três marcas, então o jogo fica empatado.

Vamos assumir que estamos jogando contra um jogador imperfeito, aquele cujo jogo às vezes está incorreto e nos permite vencer. Por enquanto, consideremos empates e perdas igualmente ruins para nós. Como podemos construir um agente de IA que encontrará as imperfeições no jogo de seu oponente e aprenderá a maximizar sua chances de ganhar?

Embora este seja um problema simples, ele não pode ser facilmente resolvido de maneira satisfatória. através de técnicas clássicas. Por exemplo, a solução clássica “minimax” da Teoria dos Jogos, não seria ideal aqui porque assume uma maneira particular de jogar pelo oponente. Por exemplo, um jogador minimax nunca chegaria a um estado de jogo do qual poderia perder, mesmo que, de fato, sempre tenha saído desse estado por causa de jogo incorreto do oponente.

Métodos clássicos de otimização para problemas de decisão sequenciais, como programação dinâmica, poderiam calcular uma solução ideal para qualquer oponente, mas exige como entrada, uma especificação completa desse oponente, incluindo as probabilidades com as quais o oponente faz cada jogada em cada estado do tabuleiro. Vamos supor que esta informação não está disponível a priori para esse problema, pois não existe para a grande maioria dos problemas de interesse prático.

Por outro lado, essas informações podem ser estimadas a partir da experiência, neste caso, jogando muitos jogos contra o oponente. O melhor que se pode fazer sobre esse problema é primeiro aprender um modelo do comportamento do oponente, até algum nível de confiança e, em seguida, aplicar a programação dinâmica para calcular uma solução ideal o modelo aproximado do oponente. No final, isso não é tão diferente de alguns dos métodos de aprendizado por reforço.

Um método evolutivo aplicado a esse problema pesquisaria diretamente o espaço de políticas possíveis para alguém com alta probabilidade de vencer o oponente. Aqui, uma política é uma regra que informa ao agente o que fazer para cada estado do jogo – todas as configurações possíveis de Xs e Os no tabuleiro três por três. Para cada política considerada, uma estimativa de sua probabilidade de vitória seria obtida jogando algum número de jogos contra o oponente. Essa avaliação direcionaria então quais políticas devem ser consideradas a seguir.

Um método evolutivo típico escalaria no espaço de políticas, gerando e avaliando sucessivamente políticas na tentativa de obter melhorias incrementais. Ou, talvez, um algoritmo genético possa ser usado para manter e avaliar uma população de políticas. Literalmente centenas de diferentes métodos de otimização podem ser aplicados.

Uma função de valor poderia ser um método eficaz nesse cenário. Aqui está como o problema do jogo da velha seria tratado com um método que faz uso de uma função de valor.

Primeiro, montaríamos uma tabela de números, uma para cada estado possível do jogo. Cada número será a estimativa mais recente da probabilidade de ganharmos nesse estado. Tratamos essa estimativa como o valor do estado, e toda a tabela é a função de valor aprendido. O estado A tem um valor mais alto que o estado B ou é considerado “melhor” do que o estado B, se a estimativa atual da probabilidade de ganharmos em A for maior do que em B. Supondo que sempre jogamos Xs, então para todos os estados com três Xs seguidos a probabilidade de ganhar é 1, porque já vencemos.

Da mesma forma, para todos os estados com três Os seguidos ou preenchidos, a probabilidade correta é 0, pois não podemos ganhar com eles. Definimos os valores iniciais de todos os outros estados para 0,5, representando que temos 50% de chance de ganhar.

Em seguida, jogamos muitos jogos contra o oponente. Para selecionar nossos movimentos, examinamos os estados que resultariam de cada um de nossos movimentos possíveis (um para cada espaço em branco no tabuleiro) e procuramos seus valores atuais na tabela. Na maioria das vezes nos movemos avidamente, selecionando o movimento que leva ao estado com maior valor, ou seja, com o maior valor de probabilidade estimada de vitória. Ocasionalmente, no entanto, selecionamos um movimento aleatoriamente. Estes são chamados movimentos exploratórios porque nos levam a ter uma experiência que, de outra forma, jamais poderíamos ter. Uma sequência de movimentos feitos e considerados durante um jogo podem ser diagramados como na figura abaixo:

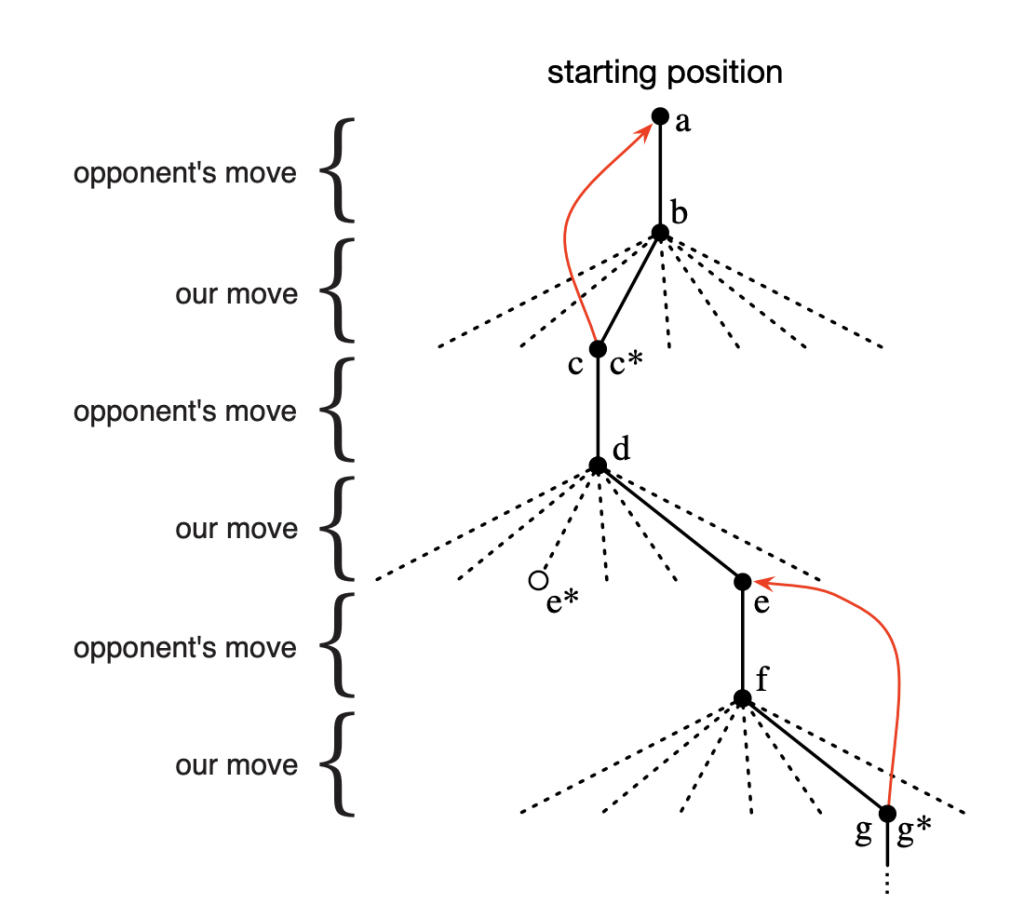
Poderíamos usar Deep Learning para realizar parte do aprendizado do processo descrito anteriormente e alimentar o agente com o resultado desse aprendizado. Isso é o que chamamos de Deep Reinforcement Learning.

Reinforcement Learning e Deep Reinforcement Learning são estudados na prática em Inteligência Artificial Aplicada a Finanças. Muitos robôs investidores usam Aprendizado por Reforço como técnica principal.

Continuaremos na parte 2. Acompanhe o próximo capítulo.

Referências:

Customizando Redes Neurais com Funções de Ativação Alternativas

A Beginner’s Guide to Deep Reinforcement Learning

What is reinforcement learning? The complete guide

Reinforcement learning

Reinforcement Learning, Second Edition

Applications of Reinforcement Learning in Real World

Practical Recommendations for Gradient-Based Training of Deep Architectures

Gradient-Based Learning Applied to Document Recognition

Neural Networks & The Backpropagation Algorithm, Explained

Recurrent neural network based language model