Capítulo 10 – As 10 Principais Arquiteturas de Redes Neurais

O Aprendizado de Máquina (Machine Learning) é necessário para resolver tarefas que são muito complexas para os humanos. Algumas tarefas são tão complexas que é impraticável, senão impossível, que os seres humanos consigam explicar todas as nuances envolvidas. Então, em vez disso, fornecemos uma grande quantidade de dados para um algoritmo de aprendizado de máquina e deixamos que o algoritmo funcione, explorando esses dados e buscando um modelo que alcance o que os Cientistas de Dados e Engenheiros de IA determinaram como objetivo. Vejamos estes dois exemplos:

– É muito difícil escrever programas que solucionem problemas como reconhecer um objeto tridimensional a partir de um novo ponto de vista em novas condições de iluminação em uma cena desordenada. Nós não sabemos qual programa de computador escrever porque não sabemos como ocorre o processo em nosso cérebro. Mesmo se tivéssemos uma boa ideia sobre como fazê-lo, o programa poderia ser incrivelmente complicado.

– É difícil escrever um programa para calcular a probabilidade de uma transação de cartão de crédito ser fraudulenta. Pode não haver regras que sejam simples e confiáveis. Precisamos combinar um número muito grande de regras fracas. A fraude é um alvo em movimento, mas o programa precisa continuar mudando.

É onde Machine Learning pode ser aplicado com sucesso. Em vez de escrever um programa à mão para cada tarefa específica, nós coletamos muitos exemplos que especificam a saída correta para uma determinada entrada. Um algoritmo de aprendizagem de máquina recebe esses exemplos e produz um programa que faz o trabalho. O programa produzido pelo algoritmo de aprendizagem pode parecer muito diferente de um programa típico escrito à mão. Pode conter milhões de números. Se o fizermos corretamente, o programa funciona para novos casos (novos dados). Se os dados mudarem, o programa também pode mudar ao treinar em novos dados. E com a redução de custos de computação (principalmente usando processamento em nuvem), grande quantidade de dados (Big Data) e processamento paralelo em GPU, temos as condições perfeitas para a evolução de Machine Learning. O maior problema, por incrível que pareça, será a falta de profissionais qualificados em número suficiente para atender as demandas do mercado.

Alguns exemplos de tarefas melhor resolvidas pela aprendizagem de máquina incluem:

Reconhecimento de padrões: objetos em cenas reais, identidades faciais ou expressões faciais, palavras escritas ou faladas.
Detecção de anomalias: sequências incomuns de transações de cartão de crédito, padrões incomuns de leituras de sensores em máquinas de uma indústria têxtil.
Previsão: preços de ações futuros ou taxas de câmbio, quais filmes uma pessoa gostaria de assistir, previsão de vendas.

Machine Learning é um campo abrangente dentro da Inteligência Artificial. Mas uma sub-área de Machine Learning, o Deep Learning (ou Redes Neurais Profundas), vem conseguindo resultados no estado da arte para as tarefas acima mencionadas. Neste capítulo você encontra As 10 Principais Arquiteturas de Redes Neurais, dentre elas as principais arquiteturas de Deep Learning.

1- Redes Multilayer Perceptrons

O Perceptron, conforme estudamos nos capítulos anteriores, é um algoritmo simples destinado a realizar a classificação binária; isto é, prevê se a entrada pertence a uma determinada categoria de interesse ou não: fraude ou não_fraude, gato ou não_gato.

Um Perceptron é um classificador linear; ou seja, é um algoritmo que classifica a entrada separando duas categorias com uma linha reta. A entrada geralmente é um vetor de recursos x multiplicado por pesos w e adicionado a um viés (ou bias) b. Aqui um exemplo do Perceptron: y = w * x + b. Um Perceptron produz uma única saída com base em várias entradas de valor real, formando uma combinação linear usando os pesos (e às vezes passando a saída através de uma função de ativação não linear).

Rosenblatt construiu um Perceptron de uma camada. Ou seja, seu algoritmo não inclui múltiplas camadas, o que permite que as redes neurais modelem uma hierarquia de recursos. Isso impede que o Perceptron consiga realizar classificação não linear, como a função XOR (um disparador do operador XOR quando a entrada exibe uma característica ou outra, mas não ambas, significa “OR exclusivo” “), como Minsky e Papert mostraram em seu livro.

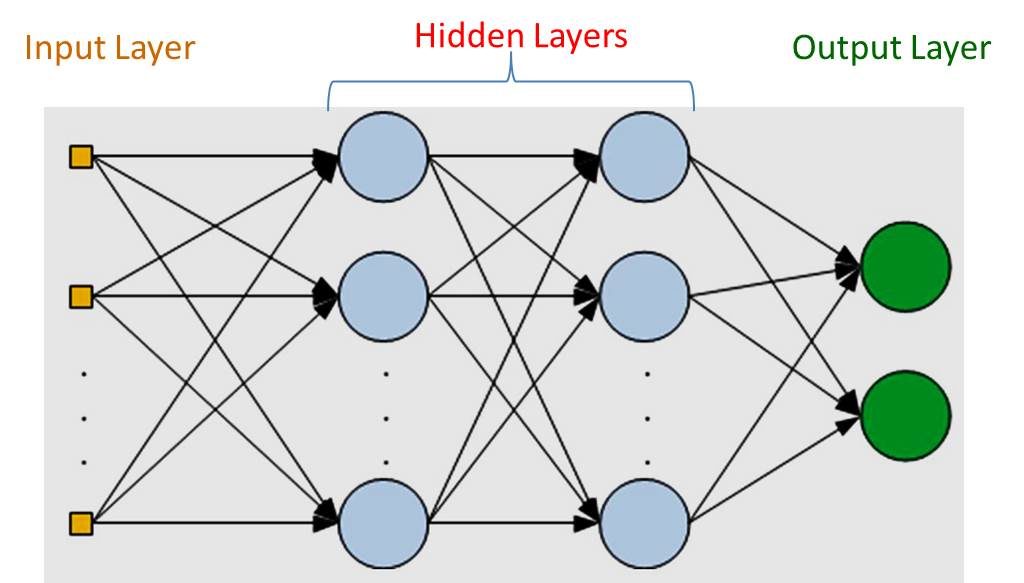
Um Multilayer Perceptron (MLP) é uma rede neural artificial composta por mais de um Perceptron. Eles são compostos por uma camada de entrada para receber o sinal, uma camada de saída que toma uma decisão ou previsão sobre a entrada, e entre esses dois, um número arbitrário de camadas ocultas que são o verdadeiro mecanismo computacional do MLP. MLPs com uma camada oculta são capazes de aproximar qualquer função contínua.

O Multilayer Perceptron é uma espécie de “Hello World” da aprendizagem profunda: uma boa forma de começar quando você está aprendendo sobre Deep Learning.

Os MLPs são frequentemente aplicados a problemas de aprendizagem supervisionados: treinam em um conjunto de pares entrada-saída e aprendem a modelar a correlação (ou dependências) entre essas entradas e saídas. O treinamento envolve o ajuste dos parâmetros, ou os pesos e bias, do modelo para minimizar o erro. O backpropagation é usado para fazer os ajustes dos pesos e de bias em relação ao erro, e o próprio erro pode ser medido de várias maneiras, inclusive pelo erro quadrático médio (MSE – Mean Squared Error).

As redes feed forward, como MLPs, são como ping-pong. Elas são principalmente envolvidas em dois movimentos, uma constante de ida e volta. Na passagem para a frente, o fluxo de sinal se move da camada de entrada através das camadas ocultas para a camada de saída e a decisão da camada de saída é medida em relação às saídas esperadas.

Na passagem para trás, usando o backpropagation e a regra da cadeia (Chain Rule), derivadas parciais da função de erro dos vários pesos e bias são reproduzidos através do MLP. Esse ato de diferenciação nos dá um gradiente, ao longo do qual os parâmetros podem ser ajustados à medida que movem o MLP um passo mais perto do erro mínimo. Isso pode ser feito com qualquer algoritmo de otimização baseado em gradiente, como descida estocástica do gradiente. A rede continua jogando aquele jogo de ping-pong até que o erro não possa mais ser reduzido (chegou ao mínimo possível). Este estado é conhecido como convergência.

Parece muita coisa? Sim, é. Veremos esse processo em mais detalhes aqui mesmo neste livro e caso queira aprender a construir modelos MLP para aplicações práticas, através de vídeos em português, clique aqui.

2- Redes Neurais Convolucionais

Em 1998, Yann LeCun e seus colaboradores desenvolveram um reconhecedor, realmente bom, para dígitos manuscritos chamado LeNet. Ele usou o backpropagation em uma rede feed forward com muitas camadas ocultas, muitos mapas de unidades replicadas em cada camada, agrupando as saídas de unidades próximas, formando uma rede ampla que pode lidar com vários caracteres ao mesmo tempo, mesmo se eles se sobrepõem e uma inteligente maneira de treinar um sistema completo, não apenas um reconhecedor. Mais tarde, esta arquitetura foi formalizada sob o nome de redes neurais convolucionais.

As Redes Neurais Convolucionais (ConvNets ou CNNs) são redes neurais artificiais profundas que podem ser usadas para classificar imagens, agrupá-las por similaridade (busca de fotos) e realizar reconhecimento de objetos dentro de cenas. São algoritmos que podem identificar rostos, indivíduos, sinais de rua, cenouras, ornitorrincos e muitos outros aspectos dos dados visuais.

As redes convolucionais realizam o reconhecimento óptico de caracteres (OCR) para digitalizar texto e tornar possível o processamento de linguagem natural em documentos analógicos e manuscritos, onde as imagens são símbolos a serem transcritos. CNNs também podem ser aplicadas a arquivos de áudio quando estes são representados visualmente como um espectrograma. Mais recentemente, as redes convolucionais foram aplicadas diretamente à análise de texto, bem como dados gráficos.

A eficácia das redes convolucionais no reconhecimento de imagem é uma das principais razões pelas quais o mundo testemunhou a eficácia do aprendizado profundo. Este tipo de rede está impulsionando grandes avanços em Visão Computacional, que tem aplicações óbvias em carros autônomos, robótica, drones, segurança, diagnósticos médicos e tratamentos para deficientes visuais.

As redes convolucionais ingerem e processam imagens como tensores e tensores são matrizes de números com várias dimensões. Eles podem ser difíceis de visualizar, então vamos abordá-los por analogia. Um escalar é apenas um número, como 7; um vetor é uma lista de números (por exemplo, [7,8,9]); e uma matriz é uma grade retangular de números que ocupam várias linhas e colunas como uma planilha. Geometricamente, se um escalar é um ponto de dimensão zero, então um vetor é uma linha unidimensional, uma matriz é um plano bidimensional, uma pilha de matrizes é um cubo tridimensional e quando cada elemento dessas matrizes tem uma pilha de mapas de recursos ligados a ele, você entra na quarta dimensão. Calma, não se desespere (ainda). Veremos isso mais a frente com calma, quando estudarmos exclusivamente esta arquitetura. Em nossos cursos na Data Science Academy incluímos aulas completas sobre Álgebra Linear, onde escalares, vetores, matrizes e tensores são estudados na teoria e prática, pois este conhecimento é fundamental na construção de redes neurais profundas.

A primeira coisa a saber sobre redes convolucionais é que elas não percebem imagens como os humanos. Portanto, você terá que pensar de uma maneira diferente sobre o que uma imagem significa quando é alimentada e processada por uma rede convolucional.

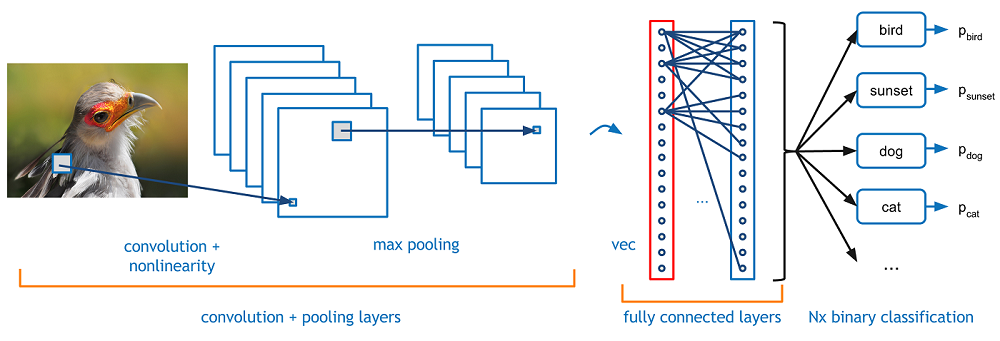
As redes convolucionais percebem imagens como volumes; isto é, objetos tridimensionais, em vez de estruturas planas a serem medidas apenas por largura e altura. Isso porque as imagens de cores digitais têm uma codificação vermelho-verde-azul (RGB – Red-Green-Blue), misturando essas três cores para produzir o espectro de cores que os seres humanos percebem. Uma rede convolucional recebe imagens como três estratos separados de cores empilhados um em cima do outro.

Assim, uma rede convolucional recebe uma imagem como uma caixa retangular cuja largura e altura são medidas pelo número de pixels ao longo dessas dimensões e cuja profundidade é de três camadas profundas, uma para cada letra em RGB. Essas camadas de profundidade são referidas como canais.

À medida que as imagens se movem através de uma rede convolucional, descrevemos em termos de volumes de entrada e saída, expressando-as matematicamente como matrizes de múltiplas dimensões dessa forma: 30x30x3. De camada em camada, suas dimensões mudam à medida que atravessam a rede neural convolucional até gerar uma série de probabilidades na camada de saída, sendo uma probabilidade para cada possível classe de saída. Aquela com maior probabilidade, será a classe definida para a imagem de entrada, um pássaro por exemplo.

Você precisará prestar muita atenção às medidas de cada dimensão do volume da imagem, porque elas são a base das operações de álgebra linear usadas para processar imagens. Poderíamos dedicar dois capítulos inteiros somente a esta arquitetura. Aliás, é o que faremos mais à frente aqui no livro e o que já fazemos na prática aqui.

3- Redes Neurais Recorrentes

As redes recorrentes são um poderoso conjunto de algoritmos de redes neurais artificiais especialmente úteis para o processamento de dados sequenciais, como som, dados de séries temporais ou linguagem natural. Uma versão de redes recorrentes foi usada pelo DeepMind no projeto de videogames com agentes autônomos.

As redes recorrentes diferem das redes feed forward porque incluem um loop de feedback, pelo qual a saída do passo n-1 é alimentada de volta à rede para afetar o resultado do passo n, e assim por diante para cada etapa subsequente. Por exemplo, se uma rede é exposta a uma palavra letra por letra, e é solicitado a adivinhar cada letra a seguir, a primeira letra de uma palavra ajudará a determinar o que uma rede recorrente pensa que a segunda letra pode ser.

Isso difere de uma rede feed forward, que aprende a classificar cada número manuscrito por exemplo, independentemente, e de acordo com os pixels de que é exposto a partir de um único exemplo, sem se referir ao exemplo anterior para ajustar suas previsões. As redes feed forward aceitam uma entrada por vez e produzem uma saída. As redes recorrentes não enfrentam a mesma restrição um-para-um.

Embora algumas formas de dados, como imagens, não pareçam ser sequenciais, elas podem ser entendidas como sequências quando alimentadas em uma rede recorrente. Considere uma imagem de uma palavra manuscrita. Assim como as redes recorrentes processam a escrita manual, convertendo cada imagem em uma letra e usando o início de uma palavra para adivinhar como essa palavra terminará, então as redes podem tratar parte de qualquer imagem como letras em uma sequência. Uma rede neural que percorre uma imagem grande pode aprender a partir de cada região, o que as regiões vizinhas, são mais prováveis de ser.

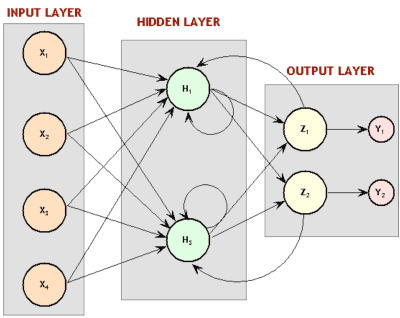
As redes recorrentes e as redes feed forward “lembram” algo sobre o mundo, modelando os dados que estão expostos. Mas elas se lembram de maneiras muito diferentes. Após o treinamento, a rede feed forward produz um modelo estático dos dados e esse modelo pode então aceitar novos exemplos e classificá-los ou agrupá-los com precisão.

Em contraste, as redes recorrentes produzem modelos dinâmicos – ou seja, modelos que mudam ao longo do tempo – de formas que produzem classificações precisas dependentes do contexto dos exemplos que estão expostos.

Para ser preciso, um modelo recorrente inclui o estado oculto que determinou a classificação anterior em uma série. Em cada etapa subsequente, esse estado oculto é combinado com os dados de entrada do novo passo para produzir a) um novo estado oculto e, em seguida, b) uma nova classificação. Cada estado oculto é reciclado para produzir seu sucessor modificado.

As memórias humanas também são conscientes do contexto, reciclando a consciência de estados anteriores para interpretar corretamente novos dados. Por exemplo, vamos considerar dois indivíduos. Um está ciente de que ele está perto da casa de Bob. O outro está ciente de que entrou em um avião. Eles interpretarão os sons “Oi Bob!” de duas formas muito diferentes, precisamente porque retém um estado oculto afetado por suas memórias de curto prazo e sensações precedentes.

Diferentes lembranças de curto prazo devem ser recontadas em momentos diferentes, a fim de atribuir o significado certo à entrada atual. Algumas dessas memórias terão sido forjadas recentemente e outras memórias terão forjado muitos passos antes de serem necessários. A rede recorrente que efetivamente associa memórias e entrada remota no tempo é chamada de Memória de Longo Prazo (LSTM), a qual veremos em seguida.

4- Long Short-Term Memory (LSTM)

Em meados dos anos 90, a proposta dos pesquisadores alemães Sepp Hochreiter e Juergen Schmidhuber apresentou uma variação da rede recorrente com as chamadas unidades de Long Short-Term Memory, como uma solução para o problema do vanishing gradient, problema comum em redes neurais recorrentes.

Os LSTMs ajudam a preservar o erro que pode ser copiado por tempo e camadas. Ao manter um erro mais constante, eles permitem que as redes recorrentes continuem aprendendo durante vários passos de tempo (mais de 1000), abrindo assim um canal para vincular causas e efeitos remotamente. Este é um dos desafios centrais para a aprendizagem de máquina e a IA, uma vez que os algoritmos são frequentemente confrontados por ambientes onde os sinais de recompensa são escassos e atrasados, como a própria vida. (Os pensadores religiosos abordaram este mesmo problema com ideias de karma ou recompensas divinas, teorizando consequências invisíveis e distantes para nossas ações).

Os LSTMs contêm informações fora do fluxo normal da rede recorrente em uma célula fechada. As informações podem ser armazenadas, escritas ou lidas a partir de uma célula, como dados na memória de um computador. A célula toma decisões sobre o que armazenar, e quando permitir leituras, gravações e exclusões, através de portões abertos e fechados. Ao contrário do armazenamento digital em computadores, no entanto, esses portões são analógicos, implementados com a multiplicação de elementos por sigmóides, que estão todos na faixa de 0-1. Analógico tem a vantagem sobre o digital de ser diferenciável e, portanto, adequado para backpropagation.

Esses portões atuam sobre os sinais que recebem e, de forma semelhante aos nós da rede neural, eles bloqueiam ou transmitem informações com base em sua força e importação, que eles filtram com seus próprios conjuntos de pesos. Esses pesos, como os pesos que modulam a entrada e estados ocultos, são ajustados através do processo de aprendizagem das redes recorrentes. Ou seja, as células aprendem quando permitir que os dados entrem, saiam ou sejam excluídos através do processo iterativo de fazer suposições, calculando o erro durante o backpropagation e ajustando pesos através da descida do gradiente.

O diagrama abaixo ilustra como os dados fluem através de uma célula de memória e são controlados por seus portões.

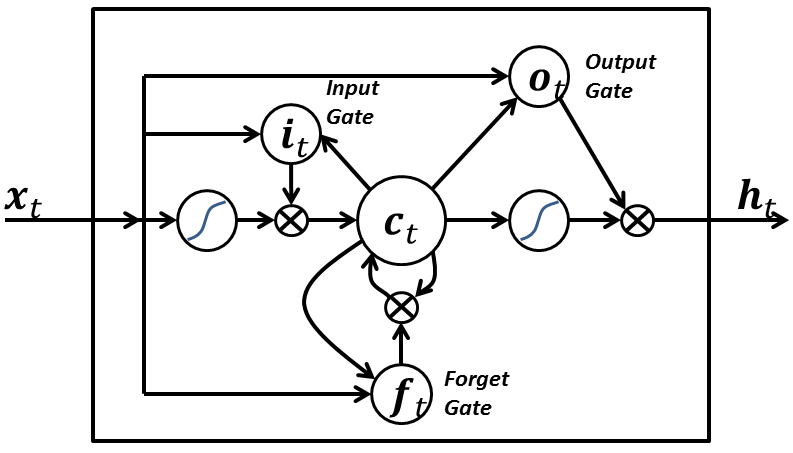
Os LSTM’s possuem muitas aplicações práticas, incluindo processamento de linguagem natural, geração automática de texto e análise de séries temporais. Caso queira ver esses exemplos na prática, clique aqui. Teremos um capítulo inteiro dedicado aos LSTM’s aqui no livro.

5- Redes de Hopfield

Redes recorrentes de unidades não lineares geralmente são muito difíceis de analisar. Elas podem se comportar de muitas maneiras diferentes: se estabelecer em um estado estável, oscilar ou seguir trajetórias caóticas que não podem ser preditas no futuro. Uma Rede Hopfield é composta por unidades de limite binário com conexões recorrentes entre elas. Em 1982, John Hopfield percebeu que, se as conexões são simétricas, existe uma função de energia global. Cada “configuração” binária de toda a rede possui energia, enquanto a regra de decisão do limite binário faz com que a rede se conforme com um mínimo desta função de energia. Uma excelente maneira de usar esse tipo de computação é usar memórias como energia mínima para a rede neural. Usar mínimos de energia para representar memórias resulta em uma memória endereçável ao conteúdo. Um item pode ser acessado por apenas conhecer parte do seu conteúdo. É robusto contra danos no hardware.

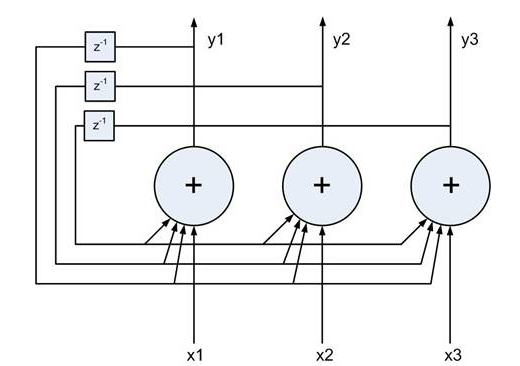
Cada vez que memorizamos uma configuração, esperamos criar um novo mínimo de energia. Mas e se dois mínimos próximos estão em um local intermediário? Isso limita a capacidade de uma Rede Hopfield. Então, como aumentamos a capacidade de uma Rede Hopfield? Os físicos adoram a ideia de que a matemática que eles já conhecem pode explicar como o cérebro funciona. Muitos artigos foram publicados em revistas de física sobre Redes Hopfield e sua capacidade de armazenamento. Eventualmente, Elizabeth Gardner descobriu que havia uma regra de armazenamento muito melhor que usa a capacidade total dos pesos. Em vez de tentar armazenar vetores de uma só vez, ela percorreu o conjunto de treinamento muitas vezes e usou o procedimento de convergência Perceptron para treinar cada unidade para ter o estado correto, dado os estados de todas as outras unidades nesse vetor. Os estatísticos chamam essa técnica de “pseudo-probabilidade”.

Existe outro papel computacional para as Redes Hopfield. Em vez de usar a rede para armazenar memórias, usamos para construir interpretações de entrada sensorial. A entrada é representada pelas unidades visíveis, a interpretação é representada pelos estados das unidades ocultas e o erro da interpretação é representado pela energia.

6- Máquinas de Boltzmann

Uma Máquina de Boltzmann é um tipo de rede neural recorrente estocástica. Pode ser visto como a contrapartida estocástica e generativa das Redes Hopfield. Foi uma das primeiras redes neurais capazes de aprender representações internas e é capaz de representar e resolver problemas combinatórios difíceis.

O objetivo do aprendizado do algoritmo da Máquina de Boltzmann é maximizar o produto das probabilidades que a Máquina de Boltzmann atribui aos vetores binários no conjunto de treinamento. Isso equivale a maximizar a soma das probabilidades de log que a Máquina de Boltzmann atribui aos vetores de treinamento. Também é equivalente a maximizar a probabilidade de obtermos exatamente os N casos de treinamento se fizéssemos o seguinte: 1) Deixar a rede se estabelecer em sua distribuição estacionária no tempo N diferente, sem entrada externa e 2) Mudar o vetor visível uma vez em cada passada.

Um procedimento eficiente de aprendizado de mini-lote foi proposto para as Máquinas de Boltzmann por Salakhutdinov e Hinton em 2012.

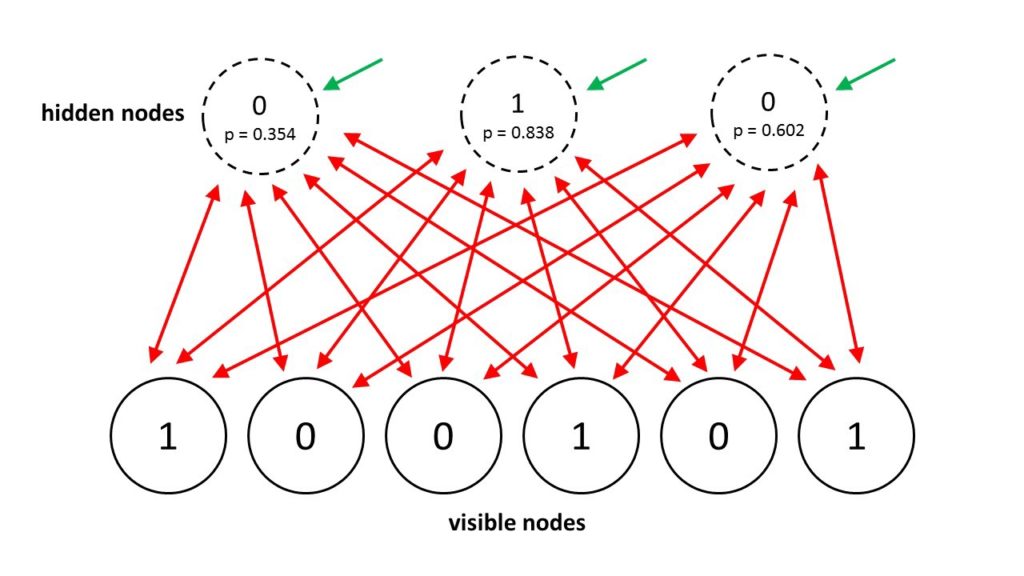
Em uma Máquina de Boltzmann geral, as atualizações estocásticas de unidades precisam ser sequenciais. Existe uma arquitetura especial que permite alternar atualizações paralelas que são muito mais eficientes (sem conexões dentro de uma camada, sem conexões de camada ignorada). Este procedimento de mini-lote torna as atualizações da Máquina de Boltzmann mais paralelas. Isso é chamado de Deep Boltzmann Machines (DBM), uma Máquina de Boltzmann geral, mas com muitas conexões ausentes.

Em 2014, Salakhutdinov e Hinton apresentaram outra atualização para seu modelo, chamando-o de Máquinas Boltzmann Restritas. Elas restringem a conectividade para facilitar a inferência e a aprendizagem (apenas uma camada de unidades escondidas e sem conexões entre unidades ocultas). Em um RBM, é preciso apenas um passo para alcançar o equilíbrio.

7- Deep Belief Network

O backpropagation é considerado o método padrão em redes neurais artificiais para calcular a contribuição de erro de cada neurônio após processar um lote de dados (teremos um capítulo inteiro sobre isso). No entanto, existem alguns problemas importantes no backpropagation. Em primeiro lugar, requer dados de treinamento rotulados; enquanto quase todos os dados estão sem rótulos. Em segundo lugar, o tempo de aprendizagem não escala bem, o que significa que é muito lento em redes com múltiplas camadas ocultas. Em terceiro lugar, pode ficar preso em um “local optima”. Portanto, para redes profundas, o backpropagation está longe de ser ótimo.

Para superar as limitações do backpropagation, os pesquisadores consideraram o uso de abordagens de aprendizado sem supervisão. Isso ajuda a manter a eficiência e a simplicidade de usar um método de gradiente para ajustar os pesos, mas também usá-lo para modelar a estrutura da entrada sensorial. Em particular, eles ajustam os pesos para maximizar a probabilidade de um modelo gerador ter gerado a entrada sensorial. A questão é que tipo de modelo generativo devemos aprender? Pode ser um modelo baseado em energia como uma Máquina de Boltzmann? Ou um modelo causal feito de neurônios? Ou um híbrido dos dois?

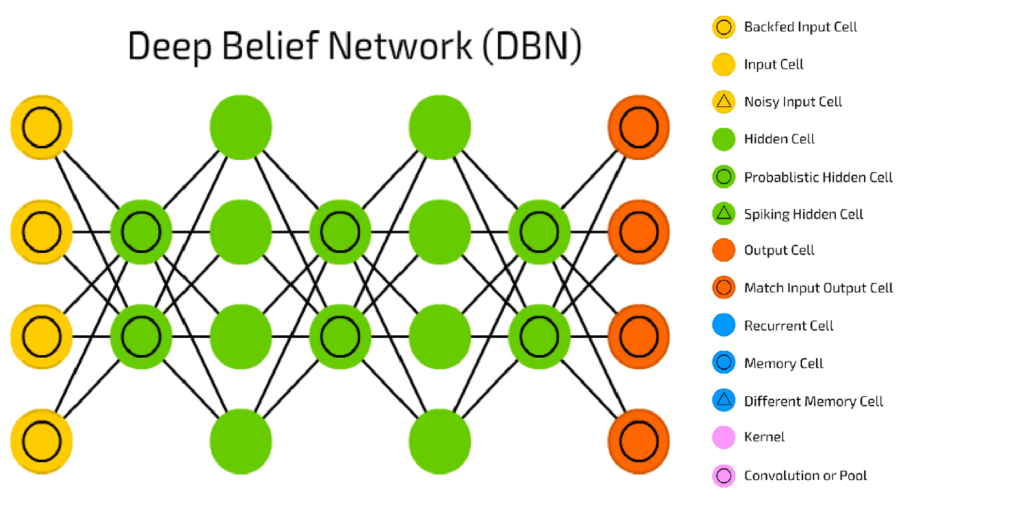
Uma Deep Belief Network pode ser definida como uma pilha de Máquinas de Boltzmann Restritas (RBM – Restricted Boltzmann Machines), em que cada camada RBM se comunica com as camadas anterior e posterior. Os nós de qualquer camada única não se comunicam lateralmente.

Esta pilha de RBMs pode terminar com uma camada Softmax para criar um classificador, ou simplesmente pode ajudar a agrupar dados não gravados em um cenário de aprendizado sem supervisão.

Com a exceção das camadas inicial e final, cada camada em uma Deep Belief Network tem uma função dupla: ela serve como a camada oculta para os nós que vem antes, e como a camada de entrada (ou “visível”) para a nós que vem depois. É uma rede construída de redes de camada única.

As Deep Belief Networks são usadas para reconhecer, agrupar e gerar imagens, sequências de vídeos e dados de captura de movimento. Outra aplicação das Deep Belief Networks é no Processamento de Linguagem Natural. Esse tipo de rede foi apresentado por Geoff Hinton e seus alunos em 2006.

8- Deep Auto-Encoders

Um Deep Auto-Encoder é composto por duas redes simétricas Deep Belief que tipicamente têm quatro ou cinco camadas rasas que representam a metade da codificação (encoder) da rede e o segundo conjunto de quatro ou cinco camadas que compõem a metade da decodificação (decoder).

As camadas são Máquinas de Boltzmann Restritas, os blocos de construção das Deep Belief Networks, com várias peculiaridades que discutiremos abaixo. Aqui está um esquema simplificado da estrutura de um Deep Auto-Encoder:

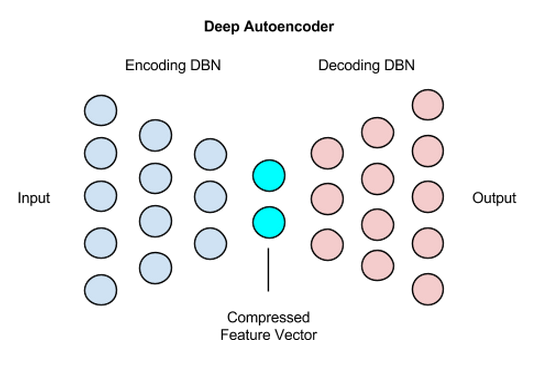
Os Deep Auto-Encoders são uma maneira muito agradável de reduzir a dimensionalidade não linear devido a alguns motivos: eles fornecem mapeamentos flexíveis em ambos os sentidos. O tempo de aprendizagem é linear (ou melhor) no número de casos de treinamento. E o modelo de codificação final é bastante compacto e rápido. No entanto, pode ser muito difícil otimizar Deep Auto-Encoders usando backpropagation. Com pequenos pesos iniciais, o gradiente do backpropagation morre. Mas temos maneiras de otimizá-las, usando o pré-treinamento camada-por-camada sem supervisão ou apenas inicializando os pesos com cuidado.

Os Deep Auto-Encoders são úteis na modelagem de tópicos ou modelagem estatística de tópicos abstratos que são distribuídos em uma coleção de documentos. Isso, por sua vez, é um passo importante em sistemas de perguntas e respostas como o IBM Watson.

Em resumo, cada documento em uma coleção é convertido em um Bag-of-Words (ou seja, um conjunto de contagens de palavras) e essas contagens de palavras são dimensionadas para decimais entre 0 e 1, o que pode ser pensado como a probabilidade de uma palavra ocorrer no documento.

As contagens de palavras em escala são então alimentadas em uma Deep Belief Network, uma pilha de Máquinas de Boltzmann Restritas, que elas mesmas são apenas um subconjunto de Autoencoders. Essas Deep Belief Networks, ou DBNs, comprimem cada documento para um conjunto de 10 números através de uma série de transformações sigmóides que o mapeiam no espaço de recursos.

O conjunto de números de cada documento, ou vetor, é então introduzido no mesmo espaço vetorial, e sua distância de qualquer outro vetor de documento medido. Em termos aproximados, os vetores de documentos próximos se enquadram no mesmo tópico. Por exemplo, um documento poderia ser a “pergunta” e outros poderiam ser as “respostas”, uma combinação que o software faria usando medidas de espaço vetorial.

Em resumo, existem agora muitas maneiras diferentes de fazer pré-treinamento camada-por-camada de recursos. Para conjuntos de dados que não possuem um grande número de casos rotulados, o pré-treinamento ajuda a aprendizagem discriminativa subsequente. Para conjuntos de dados muito grandes e rotulados, não é necessário inicializar os pesos utilizados na aprendizagem supervisionada usando pré-treinamento não supervisionado, mesmo para redes profundas. O pré-treinamento foi o primeiro bom caminho para inicializar os pesos para redes profundas, mas agora existem outras formas. Mas se construímos redes muito maiores, precisaremos de pré-treinamento novamente! Se quiser aprender a construir Deep Auto-Encoders em Python, clique aqui.

9- Generative Adversarial Network

As Generative Adversarial Networks (GANs) são arquiteturas de redes neurais profundas compostas por duas redes, colocando uma contra a outra (daí o nome, “adversária”).

Os GANs foram introduzidos em um artigo de Ian Goodfellow e outros pesquisadores da Universidade de Montreal no Canadá, incluindo Yoshua Bengio, em 2014. Referindo-se aos GANs, o diretor de pesquisa de IA do Facebook, Yann LeCun, chamou de treinamento adversário “a ideia mais interessante nos últimos 10 anos em Machine Learning”.

O potencial de GANs é enorme, porque eles podem aprender a imitar qualquer distribuição de dados. Ou seja, os GANs podem ser ensinados a criar mundos estranhamente semelhantes aos nossos em qualquer domínio: imagens, música, fala, prosa. Eles são artistas robôs em um sentido, e sua produção é impressionante – até mesmo pungente.

Para entender os GANs, você deve saber como os algoritmos geradores funcionam, e para isso, contrastá-los com algoritmos discriminatórios é útil. Os algoritmos discriminatórios tentam classificar dados de entrada; isto é, dados os recursos de uma instância de dados, eles predizem um rótulo ou categoria a que esses dados pertencem.

Por exemplo, tendo em conta todas as palavras em um e-mail, um algoritmo discriminatório pode prever se a mensagem é spam ou not_spam. O spam é um dos rótulos, e o saco de palavras (Bag of Words) coletadas do e-mail são os recursos que constituem os dados de entrada. Quando este problema é expresso matematicamente, o rótulo é chamado y e os recursos são chamados de x. A formulação p (y | x) é usada para significar “a probabilidade de y dado x”, que neste caso seria traduzido para “a probabilidade de um email ser spam com as palavras que contém”.

Portanto, algoritmos discriminatórios mapeiam recursos para rótulos. Eles estão preocupados apenas com essa correlação. Uma maneira de pensar sobre algoritmos generativos é que eles fazem o contrário. Em vez de prever um rótulo com determinados recursos, eles tentam prever os recursos com um determinado rótulo.

A questão que um algoritmo gerador tenta responder é: assumir que este e-mail é spam, qual a probabilidade dos recursos? Enquanto os modelos discriminativos se preocupam com a relação entre y e x, os modelos generativos se preocupam com “como você obtém x”. Eles permitem que você capture p (x | y), a probabilidade de x dado y, ou a probabilidade de características oferecidas em uma classe . (Dito isto, os algoritmos geradores também podem ser usados como classificadores, embora eles podem fazer mais do que categorizar dados de entrada.)

Outra maneira de pensar sobre isso é distinguir discriminativo de gerador assim:

Modelos discriminativos aprendem o limite entre as classes
Modelos generativos modelam a distribuição de classes individuais

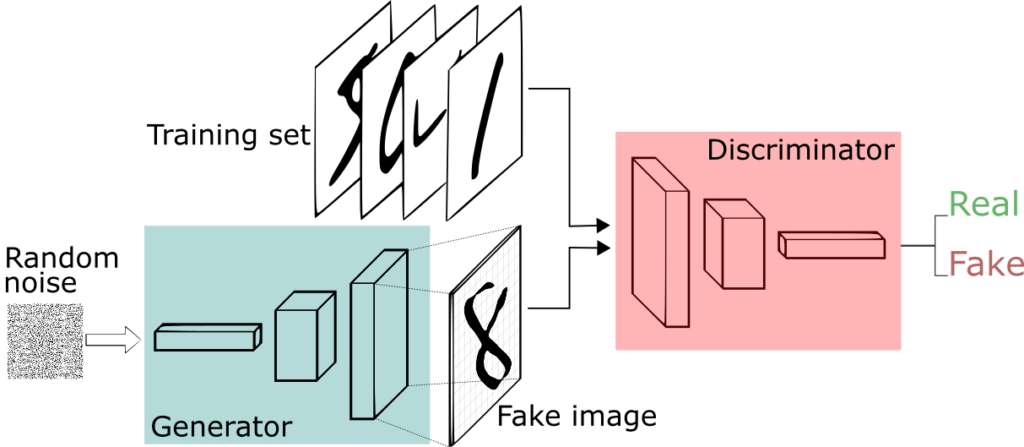
Uma rede neural, chamada de gerador, gera novas instâncias de dados, enquanto a outra, o discriminador, as avalia por autenticidade; ou seja, o discriminador decide se cada instância de dados que revisa pertence ao conjunto de dados de treinamento real ou não.

Digamos que estamos tentando fazer algo mais banal do que imitar a Mona Lisa. Vamos gerar números escritos à mão como os encontrados no conjunto de dados MNIST, que é retirado do mundo real. O objetivo do discriminador, quando mostrado uma instância do verdadeiro conjunto de dados MNIST, é reconhecê-los como autênticos.

Enquanto isso, o gerador está criando novas imagens que passa para o discriminador. Isso acontece com a esperança de que eles, também, sejam considerados autênticos, embora sejam falsos. O objetivo do gerador é gerar dígitos escritos à mão por si mesmo. O objetivo do discriminador é identificar as imagens provenientes do gerador como falsas.

Aqui estão os passos que um GAN realiza:

O gerador recebe números aleatórios e retorna uma imagem.
Essa imagem gerada é alimentada no discriminador ao lado de um fluxo de imagens tiradas do conjunto de dados real.
O discriminador assume imagens reais e falsas e retorna probabilidades, um número entre 0 e 1, com 1 representando uma previsão de autenticidade e 0 representando falsas.

Então você tem um loop de feedback duplo:

O discriminador está em um loop de feedback com as imagens verdadeiras, que conhecemos.
O gerador está em um loop de feedback com o discriminador.

Quer aprender como construir GANs, uma das arquiteturas mais incríveis de Deep Learning, 100% em português e 100% online, para gerar imagens de forma automática? Clique aqui.

10- Deep Neural Network Capsules

No final de 2017, Geoffrey Hinton e sua equipe publicaram dois artigos que introduziram um novo tipo de rede neural chamada Capsules. Além disso, a equipe publicou um algoritmo, denominado roteamento dinâmico entre cápsulas, que permite treinar essa rede.

Para todos na comunidade de Deep Learning, esta é uma grande notícia, e por várias razões. Em primeiro lugar, Hinton é um dos fundadores do Deep Learning e um inventor de inúmeros modelos e algoritmos que hoje são amplamente utilizados. Em segundo lugar, esses artigos apresentam algo completamente novo, e isso é muito emocionante porque provavelmente estimulará a onda adicional de pesquisas e aplicativos muito inovadores.

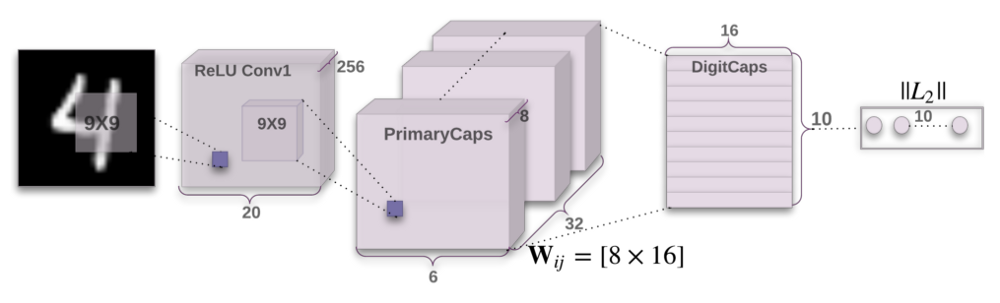
As Capsules introduzem um novo bloco de construção que pode ser usado na aprendizagem profunda para modelar melhor as relações hierárquicas dentro da representação do conhecimento interno de uma rede neural. A intuição por trás deles é muito simples e elegante.

Hinton e sua equipe propuseram uma maneira de treinar essa rede composta de cápsulas e treinou-a com êxito em um conjunto de dados simples, alcançando desempenho de ponta. Isso é muito encorajador. No entanto, há desafios. As implementações atuais são muito mais lentas do que outros modelos modernos de aprendizado profundo. O tempo mostrará se as redes Capsules podem ser treinadas de forma rápida e eficiente. Além disso, precisamos ver se elas funcionam bem em conjuntos de dados mais difíceis e em diferentes domínios.

Em qualquer caso, a rede Capsule é um modelo muito interessante e já funcionando, que definitivamente se desenvolverá ao longo do tempo e contribuirá para uma maior expansão de aplicações de aprendizagem profunda.

Incluímos as Capsules entre as 10 principais arquiteturas de redes neurais, pois elas representam a inovação e o avanço na incrível e vibrante área de Deep Learning e sistemas de Inteligência Artificial. Profissionais que realmente desejem abraçar IA como carreira, devem estar atentos aos movimentos e inovações na área.

Esta não é uma lista definitiva de arquiteturas e existem outras, tais como Word2Vec, Doc2vec, Neural Embeddings e variações das arquiteturas aqui apresentadas, como Denoising Autoencoders, Variational Autoencoders, além de outras categorias como Deep Reinforcement Learning. Exatamente para auxiliar aqueles que buscam conhecimento de ponta 100% em português e 100% online, que nós criamos a Formação Engenheiro de IA, o único programa do Brasil completo, com todas as ferramentas que o aluno precisa para aprender a trabalhar com IA de forma eficiente. O aluno aprende programação paralela em GPU, Deep Learning e seus frameworks, estuda as principais arquiteturas com aplicações práticas e desenvolve aplicações de Visão Computacional e Processamento de Linguagem Natural. Clique aqui e veja mais detalhes sobre o programa.

Isso conclui a primeira parte deste livro, com uma introdução ao universo do Deep Learning. No próximo capítulo começaremos a ver as redes neurais em ação. Até lá.

Referências:

Machine Learning

The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

Pattern Recognition and Machine Learning

Understanding Activation Functions in Neural Networks

Multilayer Perceptrons

Long Short-Term Memory

Long Short-Term Memory Neural Computation

The Unreasonable Effectiveness of Recurrent Neural Networks

Perceptrons, Expanded Edition

The 8 Neural Network Architectures Machine Learning Researchers Need to Learn

Dynamic Routing Between Capsules