Capítulo 11 – Design De Uma Rede Neural Para Reconhecimento de Dígitos
Na primeira parte deste livro online, durante os 10 primeiros capítulos, definimos e estudamos o universo das redes neurais artificias. Neste ponto você já deve ter uma boa compreensão sobre que são estes algoritmos e como podem ser usados, além da importância das redes neurais para a construção de sistemas de Inteligência Artificial. Estamos prontos para iniciar a construção de redes neurais e na sequência estudaremos as arquiteturas mais avançadas. Vamos começar definindo o Design De Uma Rede Neural Para Reconhecimento de Dígitos.
Nossa primeira tarefa será construir uma rede neural para reconhecer caligrafia, ou seja, dígitos escritos à mão que foram digitalizados em imagens no computador. Por que vamos começar com este tipo de tarefa? Porque ela permite percorrer todas as etapas e procedimentos matemáticos de uma rede neural, sendo portanto uma excelente introdução. Vamos começar?
Se você acompanha os cursos na Data Science Academy já sabe que: antes de pensar em escrever sua primeira linha de código, é preciso definir claramente o problema a ser resolvido. A tecnologia existe para resolver problemas e a definição clara do objetivo é o ponto de partida de qualquer projeto de sucesso! Neste capítulo definiremos o problema a ser resolvido, nesse caso o reconhecimento de dígitos manuscritos.
Podemos dividir o problema de reconhecer os dígitos manuscritos em dois sub-problemas. Primeiro, precisamos encontrar uma maneira de quebrar uma imagem que contenha muitos dígitos em uma sequência de imagens separadas, cada uma contendo um único dígito. Por exemplo, gostaríamos de quebrar a imagem:
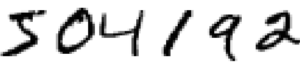
em seis imagens separadas:
![]()
Nós, humanos, resolvemos esse problema de segmentação com facilidade, mas é um desafio para um programa de computador dividir corretamente a imagem. Uma vez que a imagem foi segmentada, o programa precisa classificar cada dígito individual. Então, por exemplo, gostaríamos que nosso programa reconhecesse automaticamente que o primeiro dígito acima é um 5:
![]()
Vamos nos concentrar em escrever um programa para resolver o segundo problema, isto é, classificar dígitos individuais. O problema da segmentação não é tão difícil de resolver, uma vez que você tenha uma boa maneira de classificar os dígitos individuais. Existem muitas abordagens para resolver o problema de segmentação. Uma abordagem é testar muitas maneiras diferentes de segmentar a imagem, usando o classificador de dígitos individuais para marcar cada segmentação de teste. Uma segmentação de teste obtém uma pontuação alta se o classificador de dígitos individuais estiver confiante de sua classificação em todos os segmentos e uma pontuação baixa se o classificador tiver muitos problemas em um ou mais segmentos. A ideia é que, se o classificador estiver tendo problemas em algum lugar, provavelmente está tendo problemas porque a segmentação foi escolhida incorretamente. Essa ideia e outras variações podem ser usadas para resolver o problema de segmentação. Então, em vez de se preocupar com a segmentação, nos concentraremos no desenvolvimento de uma rede neural que pode resolver o problema mais interessante e difícil, ou seja, reconhecer dígitos individuais manuscritos.
Para reconhecer dígitos individuais, usaremos uma rede neural de três camadas:
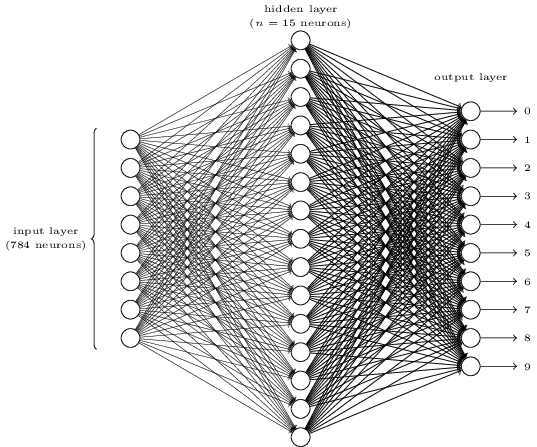
A camada de entrada da rede contém neurônios que codificam os valores dos pixels de entrada. Conforme iremos discutir no próximo capítulo, nossos dados de treinamento para a rede consistirão em muitas imagens de 28 por 28 pixels de dígitos manuscritos digitalizados e, portanto, a camada de entrada contém 28 × 28 = 784 neurônios (Nota: uma imagem nada mais é do que uma matriz, nesse caso de dimensões 28×28, que iremos converter em um vetor cujo tamanho será 784, onde cada item representa um pixel na imagem). Os pixels de entrada são de escala de cinza, com um valor de 0.0 representando branco e um valor de 1.0 representando preto. Valores intermediários representam tonalidades gradualmente escurecidas de cinza.
A segunda camada da rede é uma camada oculta. Representaremos o número de neurônios nesta camada oculta por n, e vamos experimentar diferentes valores para n. O exemplo mostrado acima ilustra uma pequena camada oculta, contendo apenas n = 15 neurônios.
A camada de saída da rede contém 10 neurônios. Se o primeiro neurônio “disparar” (for ativado), ou seja, tiver uma saída ≈ 1, então isso indicará que a rede acha que o dígito é 0. Se o segundo neurônio “disparar” (for ativado), isso indicará que a rede pensa que o dígito é um 1. E assim por diante. Em resumo, vamos numerar os neurônios de saída de 0 a 9 e descobrimos qual neurônio possui o maior valor de ativação. Se esse neurônio é, digamos, neurônio número 6, então nossa rede adivinhará que o dígito de entrada era um 6. E assim por diante para os outros neurônios de saída.
Você pode se perguntar por que usamos 10 neurônios de saída. Afinal, o objetivo da rede é nos dizer qual dígito (0,1,2, …, 9) corresponde à imagem de entrada. Uma maneira aparentemente natural de fazer isso é usar apenas 4 neurônios de saída, tratando cada neurônio como assumindo um valor binário, dependendo se a saída do neurônio está mais próxima de 0 ou 1. Quatro neurônios são suficientes para codificar a resposta, desde que 2ˆ4 = 16 é mais do que os 10 valores possíveis para o dígito de entrada. Por que nossa rede deve usar 10 neurônios em vez disso? Isso não é ineficiente? A justificativa final é empírica: podemos experimentar ambos os projetos de rede, e verifica-se que, para este problema específico, a rede com 10 neurônios de saída aprende a reconhecer dígitos melhor do que a rede com 4 neurônios de saída. Mas isso ainda deixa a pergunta por que o uso de 10 neurônios de saída funciona melhor. Existe alguma heurística que nos diga com antecedência que devemos usar a codificação de 10 saídas em vez da codificação de 4 saídas?
Entender porque fazemos isso, ajuda a pensar sobre o que a rede neural está realmente fazendo. Considere primeiro o caso em que usamos 10 neurônios de saída. Vamos nos concentrar no primeiro neurônio de saída, aquele que está tentando decidir se o dígito é ou não 0. Ele faz isso pesando evidências da camada oculta dos neurônios. O que esses neurônios ocultos estão fazendo? Bem, vamos supor que o primeiro neurônio na camada oculta detecta ou não uma imagem como a seguinte:

Isso pode ser feito pesando fortemente pixels de entrada que se sobrepõem à imagem e apenas ponderam ligeiramente as outras entradas. De forma semelhante, suponhamos que o segundo, terceiro e quarto neurônios na camada oculta detectem se as seguintes imagens estão ou não presentes:

Como você pode ter adivinhado, essas quatro imagens juntas compõem a imagem 0 que vimos na linha de dígitos mostrada anteriormente:

Então, se todos os quatro neurônios ocultos estão disparando, podemos concluir que o dígito é um 0. Claro, esse não é o único tipo de evidência que podemos usar para concluir que a imagem era um 0 – podemos legitimamente obter um 0 em muitas outras maneiras (por exemplo, através de traduções das imagens acima, ou pequenas distorções). Mas parece seguro dizer que, pelo menos neste caso, concluiríamos que a entrada era um 0.
Supondo que a rede neural funciona assim, podemos dar uma explicação plausível sobre porque é melhor ter 10 saídas da rede, em vez de 4. Se tivéssemos 4 saídas, o primeiro neurônio de saída tentaria decidir o que mais um bit significativo do dígito representa. E não existe uma maneira fácil de relacionar esse bit mais significativo com formas simples, como as mostradas acima. As formas componentes do dígito estarão intimamente relacionadas com (digamos) o bit mais significativo na saída.
Isso tudo é apenas uma heurística. Nada diz que a rede neural de três camadas tem que operar da maneira que descrevemos, com os neurônios ocultos detectando formas de componentes simples. Talvez um algoritmo de aprendizado inteligente encontre alguma atribuição de pesos que nos permita usar apenas 4 neurônios de saída. Mas, usar uma boa heurística pode economizar muito tempo na concepção de boas arquiteturas de redes neurais.
Já temos então um design para a nossa rede neural. Agora precisamos definir como será o processo de aprendizagem do algoritmo, antes de começar a codificar nossa rede em linguagem Python. Usaremos o treinamento com Gradiente Descendente, assunto do próximo capítulo, que aliás eu não perderia por nada, se fosse você, pois aí está a “magia” por trás das redes neurais. Até lá!
Para acompanhar os próximos capítulos e reproduzir os exemplos, você deve ter o Anaconda Python instalado no seu computador. Acesse o capítulo 1 do curso gratuito Python Fundamentos Para Análise de Dados, para aprender como instalar o Anaconda.
Referências:
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Pattern Recognition and Machine Learning
Understanding Activation Functions in Neural Networks
Redes Neurais, princípios e práticas
Neural Networks and Deep Learning (alguns trechos extraídos e traduzidos com autorização do autor Michael Nielsen)

