Capítulo 16 – Algoritmo Backpropagation em Python

Depois de compreender como funciona o backpropagation, podemos agora entender o código usado em alguns capítulos anteriores para implementar o algoritmo (o qual vamos reproduzir aqui). O arquivo com o código completo pode ser encontrado aqui.

Em nosso código nós temos os métodos update_mini_batch e backprop da classe Network. Em particular, o método update_mini_batch atualiza os pesos e bias da rede calculando o gradiente para o mini_batch atual de exemplos (dados) de treinamento:

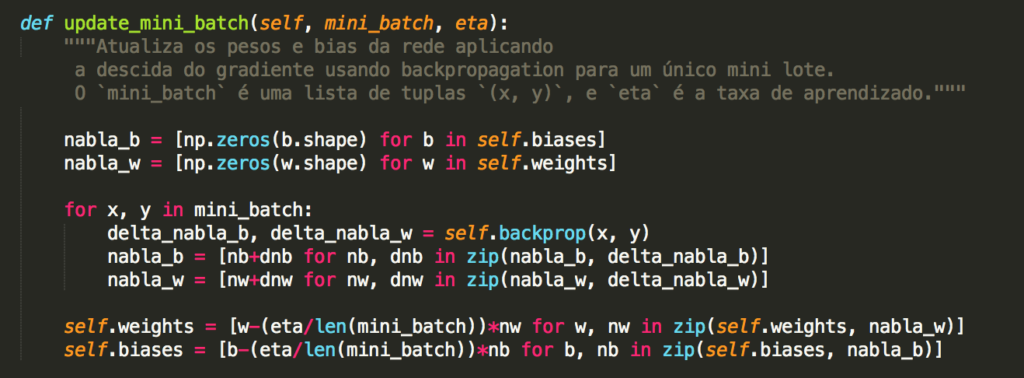
A maior parte do trabalho é feita pela linha:

delta_nabla_b, delta_nabla_w = self.backprop (x, y)

que usa o método backprop para descobrir as derivadas parciais ∂Cx / ∂blj e ∂Cx / ∂wljk. Isso invoca o algoritmo de backpropagation, que é uma maneira rápida de calcular o gradiente da função de custo. Portanto, update_mini_batch funciona simplesmente calculando esses gradientes para cada exemplo de treinamento no mini_batch e, em seguida, atualizando self.weights e self.biases adequadamente. Há uma pequena mudança – usamos uma abordagem ligeiramente diferente para indexar as camadas. Essa alteração é feita para aproveitar um recurso do Python, ou seja, o uso de índices de lista negativa para contar para trás a partir do final de uma lista, por exemplo, lst[-3] é a terceira última entrada em uma lista chamada lst. O código para backprop está abaixo, junto com algumas funções auxiliares, que são usadas para calcular a função σ, a derivada σ′ e a derivada da função de custo. Com essas inclusões, você deve ser capaz de entender o código de maneira independente:

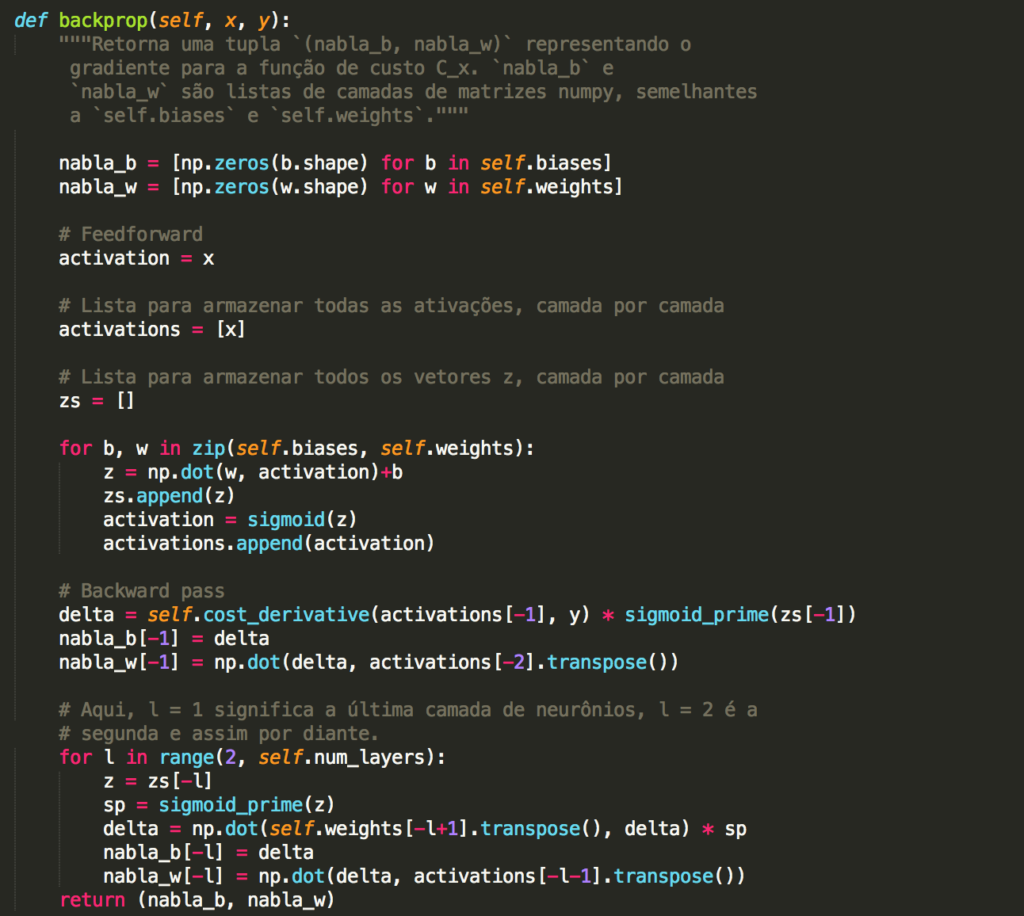
Observe o método backprop. Começamos inicalizando as matrizes de pesos (nabla_w) e bias (nabla_b) com zeros. Essas matrizes serão alimentadas com valores durante o processo de treinamento. Isso é o que a rede neural artificial efetivamente aprende. Depois de inicializar alguns objetos, temos um loop for para cada valor de b e w (que a esta altura você já sabe se trata de bias e pesos, respectivamente). Neste loop, usamos a função np.dot do Numpy para a multiplicação entre matrizes e adição do bias, colocamos o resultado na lista z e fazemos uma chamada à função de ativação Sigmóide. Ao final deste loop, teremos a lista com todas as ativações e finalizamos a passada para a frente.

Na passada para trás (Backward Pass) calculamos as derivadas e fazemos as multiplicações de matrizes mais uma vez (o funcionamento de redes neurais artificiais é baseado em um conceito elementar da Álgebra Linear, a multiplicação de matrizes). Repare que chamamos o método Transpose() para gerar a transposta da matriz e assim ajustar as dimensões antes de efetuar os cálculo. Por fim, retornamos bias e pesos.

Em que sentido backpropagation é um algoritmo rápido?

Para responder a essa pergunta, vamos considerar outra abordagem para calcular o gradiente. Imagine que é o início da pesquisa de redes neurais. Talvez seja a década de 1950 ou 1960, e você é a primeira pessoa no mundo a pensar em usar gradiente descendente para o aprendizado! Mas, para que a ideia funcione, você precisa de uma maneira de calcular o gradiente da função de custo. Você volta ao seu conhecimento de cálculo e decide se pode usar a regra da cadeia (chain rule) para calcular o gradiente. Mas depois de brincar um pouco, a álgebra parece complicada e você fica desanimado. Então você tenta encontrar outra abordagem. Você decide considerar o custo como uma função apenas dos pesos C = C(w) (voltaremos ao bias em um momento). Você numera os pesos w1, w2,… e deseja computar ∂C / ∂wj para um peso específico wj. Uma maneira óbvia de fazer isso é usar a aproximação

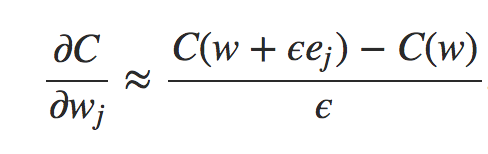
onde ϵ> 0 é um pequeno número positivo e ej é o vetor unitário na direção j. Em outras palavras, podemos estimar ∂C / ∂wj calculando o custo C para dois valores ligeiramente diferentes de wj e, em seguida, aplicando a equação. A mesma ideia nos permitirá calcular as derivadas parciais ∂C / ∂b em relação aos vieses (bias).

Essa abordagem parece muito promissora. É simples conceitualmente e extremamente fácil de implementar, usando apenas algumas linhas de código. Certamente, parece muito mais promissor do que a ideia de usar a regra da cadeia para calcular o gradiente!

Infelizmente, embora essa abordagem pareça promissora, quando você implementa o código, ele fica extremamente lento. Para entender porque, imagine que temos um milhão de pesos em nossa rede. Então, para cada peso distinto wj, precisamos computar C (w + ϵej) para calcular ∂C / ∂wj. Isso significa que, para calcular o gradiente, precisamos computar a função de custo um milhão de vezes diferentes, exigindo um milhão de passos para frente pela rede (por exemplo, treinamento). Precisamos calcular C(w) também, em um total de um milhão de vezes e em uma única passada pela rede.

O que há de inteligente no backpropagation é que ele nos permite calcular simultaneamente todas as derivadas parciais ∂C / ∂wj usando apenas uma passagem direta pela rede, seguida por uma passagem para trás pela rede. Grosso modo, o custo computacional do passe para trás é quase o mesmo que o do forward. Isso deve ser plausível, mas requer algumas análises para fazer uma declaração cuidadosa. É plausível porque o custo computacional dominante no passe para frente é multiplicado pelas matrizes de peso, enquanto no passo para trás é multiplicado pelas transpostas das matrizes de peso. Obviamente, essas operações têm um custo computacional similar. E assim, o custo total da retropropagação (backpropagation) é aproximadamente o mesmo que fazer apenas duas passagens pela rede. Compare isso com o milhão e um passe para frente que precisávamos para a abordagem que descrevi anteriormente. E assim, embora a retropropagação pareça superficialmente mais complexa do que a abordagem anterior, é na verdade muito, muito mais rápida.

Essa aceleração foi amplamente apreciada em 1986 e expandiu enormemente a gama de problemas que as redes neurais poderiam resolver. Isso, por sua vez, causou uma onda de pessoas usando redes neurais. Claro, a retropropagação não é uma panacéia. Mesmo no final da década de 1980, as pessoas enfrentavam limites, especialmente quando tentavam usar a retropropagação para treinar redes neurais profundas, ou seja, redes com muitas camadas ocultas. Mais adiante, no livro, veremos como os computadores modernos e algumas novas ideias inteligentes tornam possível usar a retropropagação para treinar redes neurais bem profundas.

Seu trabalho agora é estudar e compreender cada linha de código usada em nossa rede de amostra. Esse código é bem simples e o objetivo é mostrar a você como as coisas funcionam programaticamente. Ainda vamos treinar nossa rede, avaliar seu desempenho, otimizar algumas operações e compreender outros conceitos básicos. Temos muito mais vindo por aí! Até o próximo capítulo!

Referências:

Machine Learning

Dot Product

How the backpropagation algorithm works

Delta Rule

An overview of gradient descent optimization algorithms

Neural Networks & The Backpropagation Algorithm, Explained

Derivada

Machine Learning

The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

Gradient Descent For Machine Learning

Pattern Recognition and Machine Learning