Capítulo 17 – Cross-Entropy Cost Function
Quando um jogador de tênis está aprendendo a praticar o esporte, ele geralmente passa a maior parte do tempo desenvolvendo o movimento do corpo. Apenas gradualmente ele desenvolve as tacadas, aprende a movimentar a bola com precisão para a quadra adversária e com isso vai construindo sua técnica, que se aprimora à medida que ele pratica. De maneira semelhante, até agora nos concentramos em entender o algoritmo de retropropagação (backpropagation), a base para aprender a maioria das atividades em redes neurais. A partir de agora, estudaremos um conjunto de técnicas que podem ser usadas para melhorar nossa implementação do backpropagation e, assim, melhorar a maneira como nossas redes aprendem.
As técnicas que desenvolveremos incluem: uma melhor escolha de função de custo, conhecida como função de custo de entropia cruzada (ou Cross-Entropy Cost Function); quatro métodos de “regularização” (regularização de L1 e L2, dropout e expansão artificial dos dados de treinamento), que melhoram nossas redes para generalizar além dos dados de treinamento; um método melhor para inicializar os pesos na rede; e um conjunto de heurísticas para ajudar a escolher bons hyperparâmetros para a rede. Também vamos analisar várias outras técnicas com menos profundidade. As discussões são em grande parte independentes umas das outras e, portanto, você pode avançar se quiser. Também implementaremos muitas das técnicas em nosso código e usaremos para melhorar os resultados obtidos no problema de classificação de dígitos manuscritos estudado nos capítulos anteriores.
Naturalmente, estamos cobrindo apenas algumas das muitas técnicas que foram desenvolvidas para uso em redes neurais. A filosofia é que o melhor acesso à multiplicidade de técnicas disponíveis é o estudo aprofundado de algumas das mais importantes. Dominar essas técnicas importantes não é apenas útil por si só, mas também irá aprofundar sua compreensão sobre quais problemas podem surgir quando você usa redes neurais. Isso deixará você bem preparado para aprender rapidamente outras técnicas, conforme necessário.
A Função de Custo
A maioria de nós acha desagradável estar errado. Logo depois de começar a aprender piano, minha filha fez sua primeira apresentação diante de uma platéia. Ela estava nervosa e começou a tocar a peça com uma oitava muito baixa. Ela ficou confusa e não pôde continuar até que alguém apontasse o erro. Ela ficou muito envergonhada. Ainda que desagradável, também aprendemos rapidamente quando estamos decididamente errados. Você pode apostar que a próxima vez que ela se apresentou diante de uma platéia, ela começou na oitava correta! Em contraste, aprendemos mais lentamente quando nossos erros são menos bem definidos.
Idealmente, esperamos que nossas redes neurais aprendam rapidamente com seus erros. Mas é isso que acontece na prática? Para responder a essa pergunta, vamos dar uma olhada em um exemplo simples. O exemplo envolve um neurônio com apenas uma entrada:
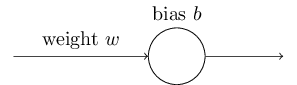
Nós vamos treinar esse neurônio para fazer algo ridiculamente fácil: obter a entrada 1 e gerar a saída 0. Claro, essa é uma tarefa tão trivial que poderíamos facilmente descobrir um peso apropriado e um viés (bias) de forma manual, sem usar um algoritmo de aprendizado. No entanto, vai nos ajudar a compreender melhor o processo de usar gradiente descendente para tentar aprender um peso e viés. Então, vamos dar uma olhada em como o neurônio aprende.
Para tornar as coisas definitivas, escolhemos o peso inicial como 0.6 e o viés inicial como 0.9. Estas são escolhas genéricas usadas como um lugar para começar a aprender, eu não as escolhi para serem especiais de alguma forma. A saída inicial do neurônio é 0.82, então um pouco de aprendizado será necessário antes que nosso neurônio se aproxime da saída desejada 0,0.
No gráfico abaixo, podemos ver como o neurônio aprende uma saída muito mais próxima de 0.0. Durante o treinamento, o modelo está realmente computando o gradiente, e usando o gradiente para atualizar o peso e o viés, e exibir o resultado. A taxa de aprendizado é η = 0.15, o que acaba sendo lento o suficiente para que possamos acompanhar o que está acontecendo, mas rápido o suficiente para que possamos obter um aprendizado substancial em apenas alguns segundos. O custo é a função de custo quadrático, C, apresentada nos capítulos anteriores. Vou lembrá-lo da forma exata da função de custo em breve.
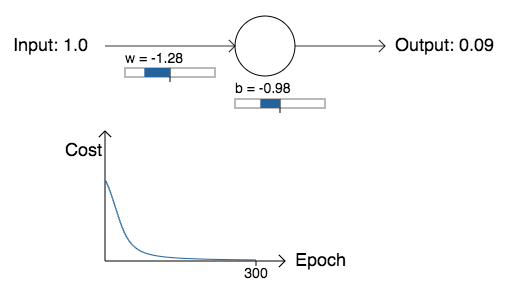
Como você pode ver, o neurônio aprende um peso e um viés que diminui o custo e dá uma saída do neurônio de cerca de 0.09 (Epoch, ou Época em português, é o número de passadas que nosso modelo faz pelos dados. A cada passada, os pesos são atualizados, o aprendizado ocorre e o custo, ou a taxa de erros, diminui). Isso não é exatamente o resultado desejado, 0.0, mas é muito bom.
Suponha, no entanto, que, em vez disso, escolhamos o peso inicial e o viés inicial como 2.0. Nesse caso, a saída inicial é 0.98, o que é muito ruim. Vamos ver como o neurônio aprende a gerar 0 neste caso:
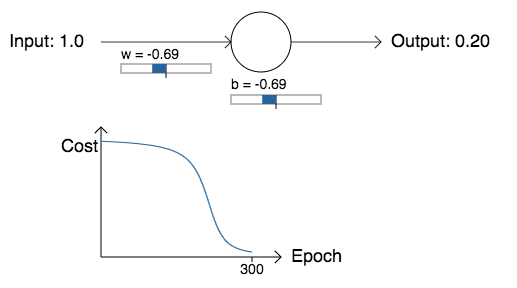
Embora este exemplo use a mesma taxa de aprendizado (η = 0.15), podemos ver que a aprendizagem começa muito mais devagar. De fato, nas primeiras 150 épocas de aprendizado, os pesos e vieses não mudam muito. Então o aprendizado entra em ação e, como em nosso primeiro exemplo, a saída do neurônio se aproxima rapidamente de 0.0.
Esse comportamento é estranho quando comparado ao aprendizado humano. Como eu disse no começo deste capítulo, muitas vezes aprendemos mais rápido quando estamos muito errados sobre algo. Mas acabamos de ver que nosso neurônio artificial tem muita dificuldade em aprender quando está muito errado – muito mais dificuldade do que quando está apenas um pouco errado. Além do mais, verifica-se que esse comportamento ocorre não apenas neste exemplo, mas em redes mais gerais. Por que aprender tão devagar? E podemos encontrar uma maneira de evitar essa desaceleração?
Para entender a origem do problema, considere que nosso neurônio aprende mudando o peso e o viés a uma taxa determinada pelas derivadas parciais da função custo, ∂C/∂w e ∂C/∂b. Então, dizer “aprender é lento” é realmente o mesmo que dizer que essas derivadas parciais são pequenas. O desafio é entender por que eles são pequenas. Para entender isso, vamos calcular as derivadas parciais. Lembre-se de que estamos usando a função de custo quadrático, que é dada por:
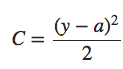
onde a é a saída do neurônio quando a entrada de treinamento x = 1 é usada, e y = 0 é a saída desejada correspondente. Para escrever isso mais explicitamente em termos de peso e viés, lembre-se que a = σ(z), onde z = wx + b. Usando a regra da cadeia para diferenciar em relação ao peso e viés, obtemos:
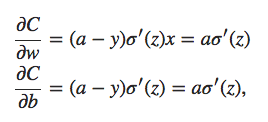
onde substitui x = 1 e y = 0. Para entender o comportamento dessas expressões, vamos olhar mais de perto o termo σ ′ (z) no lado direito. Lembre-se da forma da função σ:
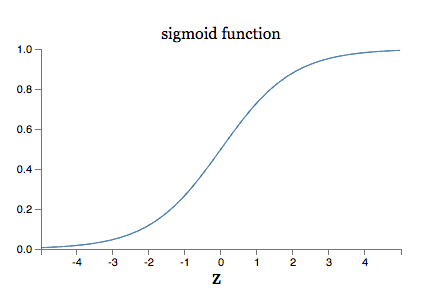
Podemos ver neste gráfico que quando a saída do neurônio é próxima de 1, a curva fica muito plana, e então σ ′ (z) fica muito pequeno. As equações acima então nos dizem que ∂C/∂w e ∂C/∂b ficam muito pequenos. Esta é a origem da desaceleração da aprendizagem. Além do mais, como veremos mais adiante, a desaceleração do aprendizado ocorre basicamente pelo mesmo motivo em redes neurais mais genéricas, não apenas neste exemplo simples.
A Função de Custo de Entropia Cruzada
Como podemos abordar a desaceleração da aprendizagem? Acontece que podemos resolver o problema substituindo o custo quadrático por uma função de custo diferente, conhecida como entropia cruzada. Para entender a entropia cruzada, vamos nos afastar um pouco do nosso modelo super-simples. Vamos supor que estamos tentando treinar um neurônio com diversas variáveis de entrada, x1, x2,…, pesos correspondentes w1, w2,… e um viés, b:
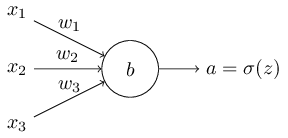
A saída do neurônio é, naturalmente, a = σ(z), onde z = ∑jwjxj + b é a soma ponderada das entradas. Nós definimos a função de custo de entropia cruzada para este neurônio assim:
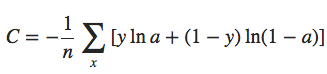
onde n é o número total de itens de dados de treinamento, a soma é sobre todas as entradas de treinamento x, e y é a saída desejada correspondente. Não é óbvio que a expressão anterior resolva o problema de desaceleração do aprendizado. De fato, francamente, nem é óbvio que faz sentido chamar isso de uma função de custo! Antes de abordar a desaceleração da aprendizagem, vamos ver em que sentido a entropia cruzada pode ser interpretada como uma função de custo.
Duas propriedades em particular tornam razoável interpretar a entropia cruzada como uma função de custo. Primeiro, não é negativo, isto é, C > 0. Para visualizar isso, observe na fórmula anterior que: (a) todos os termos individuais na soma são negativos, já que ambos os logaritmos são de números no intervalo de 0 a 1; e (b) há um sinal de menos na frente da soma.
Segundo, se a saída real do neurônio estiver próxima da saída desejada para todas as entradas de treinamento x, então a entropia cruzada será próxima de zero. Para ver isso, suponha, por exemplo, que y = 0 e a ≈ 0 para alguma entrada x. Este é um caso quando o neurônio está fazendo um bom trabalho nessa entrada. Vemos que o primeiro termo (na fórmula acima) para o custo, desaparece, desde que y = 0, enquanto o segundo termo é apenas −ln (1 − a) ≈ 0. Uma análise semelhante é válida quando y = 1 e a ≈ 1. E assim, a contribuição para o custo será baixa, desde que a saída real esteja próxima da saída desejada.
Em suma, a entropia cruzada é positiva e tende a zero, à medida que o neurônio melhora a computação da saída desejada, y, para todas as entradas de treinamento, x.
Essas são as duas propriedades que esperamos intuitivamente para uma função de custo. De fato, ambas as propriedades também são satisfeitas pelo custo quadrático. Portanto, isso é uma boa notícia para a entropia cruzada. Mas a função custo de entropia cruzada tem o benefício de que, ao contrário do custo quadrático, evita o problema de desaceleração do aprendizado. Para ver isso, vamos calcular a derivada parcial do custo de entropia cruzada em relação aos pesos. Substituímos a = σ (z) na fórmula acima e aplicamos a regra da cadeia duas vezes, obtendo:
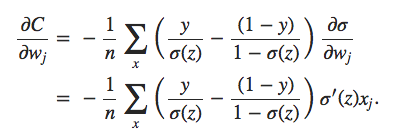
Colocando tudo em um denominador comum e simplificando, isso se torna:
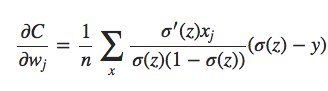
Usando a definição da função sigmóide, σ (z) = 1 / (1 + ez), e um pouco de álgebra, podemos mostrar que σ (z) = σ (z) (1 − σ (z)). Vemos que os termos σ′ (z) e σ (z) (1 − σ (z)) se cancelam na equação acima, e simplificando torna-se:
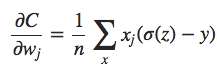
Esta é uma bela expressão. Ela nos diz que a taxa na qual o peso aprende é controlada por σ (z) −y, ou seja, pelo erro na saída. Quanto maior o erro, mais rápido o neurônio aprenderá. Isso é exatamente o que nós esperamos intuitivamente. Em particular, evita a lentidão de aprendizado causada pelo termo σ′ (z) na equação análoga para o custo quadrático. Quando usamos a entropia cruzada, o termo σ′ (z) é cancelado e não precisamos mais nos preocupar em ser pequeno. Este cancelamento é o milagre especial assegurado pela função de custo de entropia cruzada. Na verdade, não é realmente um milagre. Como veremos mais adiante, a entropia cruzada foi especialmente escolhida por ter apenas essa propriedade.
De maneira semelhante, podemos calcular a derivada parcial para o viés. Eu não vou passar por todos os detalhes novamente, mas você pode facilmente verificar que:
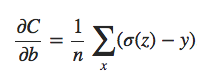
Novamente, isso evita a lentidão de aprendizado causada pelo termo σ′ (z) na equação análoga para o custo quadrático.
Agora vamos retornar ao exemplo do início deste capítulo, e explorar o que acontece quando usamos a entropia cruzada em vez do custo quadrático. Para nos reorientarmos, começaremos com o caso em que o custo quadrático foi bom, com peso inicial de 0.6 e viés inicial de 0.9. Veja o que acontece quando substituímos o custo quadrático pela entropia cruzada:
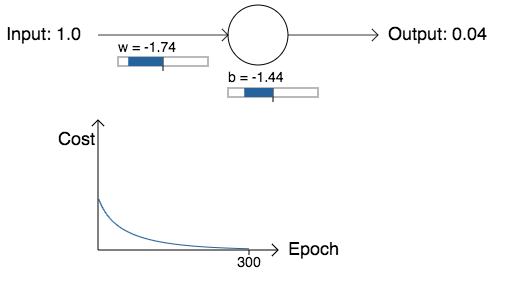
Como era de se esperar, o neurônio aprende perfeitamente bem neste caso, assim como fez anteriormente. E agora vamos olhar para o caso em que nosso neurônio ficou preso antes, com o peso e o viés ambos começando em 2.0:
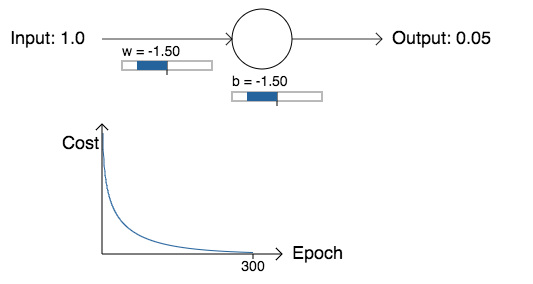
Sucesso! Desta vez, o neurônio aprendeu rapidamente, exatamente como esperávamos. Se você observar atentamente, pode ver que a inclinação da curva de custo era muito mais íngreme inicialmente do que a região plana inicial na curva correspondente para o custo quadrático. É essa inclinação que a entropia cruzada nos ajuda a resolver, impedindo-nos de ficar presos exatamente quando esperamos que nosso neurônio aprenda mais depressa, ou seja, quando o neurônio começa errado.
Eu não disse qual taxa de aprendizado foi usada nos exemplos que acabei de ilustrar. Anteriormente, com o custo quadrático, usamos η = 0.15. Deveríamos ter usado a mesma taxa de aprendizado nos novos exemplos? De fato, com a mudança na função de custo, não é possível dizer precisamente o que significa usar a “mesma” taxa de aprendizado; é uma comparação de maçãs e laranjas. Para ambas as funções de custo, simplesmente experimentei encontrar uma taxa de aprendizado que possibilitasse ver o que está acontecendo. Se você ainda estiver curioso, aqui está o resumo: usei η = 0.005 nos exemplos que acabei de fornecer.
Você pode contestar que a mudança na taxa de aprendizado torna os gráficos acima sem sentido. Quem se importa com a rapidez com que o neurônio aprende, quando a nossa escolha de taxa de aprendizado foi arbitrária, para começar ?! Mas essa objeção não procede. O ponto dos gráficos não é sobre a velocidade absoluta de aprendizagem. É sobre como a velocidade do aprendizado muda. Em particular, quando usamos o custo quadrático, a aprendizagem é mais lenta quando o neurônio está inequivocamente errado do que é mais tarde durante o treinamento, à medida que o neurônio se aproxima da saída correta; enquanto o aprendizado de entropia cruzada é mais rápido quando o neurônio está inequivocamente errado. Essas declarações não dependem de como a taxa de aprendizado é definida.
Estamos estudando a entropia cruzada para um único neurônio. No entanto, é fácil generalizar a entropia cruzada para redes multicamadas de muitos neurônios. Em particular, suponha que y = y1, y2,… são os valores desejados nos neurônios de saída, ou seja, os neurônios na camada final, enquanto aL1, aL2,… são os valores reais de saída. Então nós definimos a entropia cruzada por:
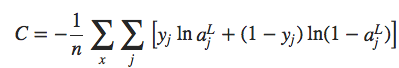
Isso é o mesmo que nossa expressão anterior, exceto que agora nós temos o ∑j somando todos os neurônios de saída. Não vou explicitamente trabalhar com uma derivação, mas deve ser plausível que o uso da expressão anterior evite uma desaceleração na aprendizagem em muitas redes de neurônios.
A propósito, estou usando o termo “entropia cruzada” de uma maneira que confundiu alguns dos primeiros leitores, já que parece superficialmente entrar em conflito com outras fontes. Em particular, é comum definir a entropia cruzada para duas distribuições de probabilidade, pj e qj, como ∑jpjlnqj. Esta definição pode ser conectada a fórmula da entropia para um neurônio mostrada anteriormente, se tratarmos um único neurônio sigmóide como saída de uma distribuição de probabilidade que consiste na ativação a do neurônio ae seu complemento 1 − a.
No entanto, quando temos muitos neurônios sigmoides na camada final, o vetor aLj de ativações não costuma formar uma distribuição de probabilidade. Como resultado, uma definição como ∑jpjlnqj não faz sentido, já que não estamos trabalhando com distribuições de probabilidade. Em vez disso, você pode pensar na fórmula da entropia para múltiplos neurônios como um conjunto somado de entropias cruzadas por neurônio, com a ativação de cada neurônio sendo interpretada como parte de uma distribuição de probabilidade de dois elementos. Sim, eu sei que isso não é simples.
Nesse sentido, a fórmula da entropia para múltiplos neurônios é uma generalização da entropia cruzada para distribuições de probabilidade.
Quando devemos usar a entropia cruzada em vez do custo quadrático? De fato, a entropia cruzada é quase sempre a melhor escolha, desde que os neurônios de saída sejam neurônios sigmóides. Para entender por que, considere que, quando estamos configurando a rede, normalmente inicializamos os pesos e vieses usando algum tipo de aleatoriedade. Pode acontecer que essas escolhas iniciais resultem na rede sendo decisivamente errada para alguma entrada de treinamento – isto é, um neurônio de saída terá saturado próximo de 1, quando deveria ser 0, ou vice-versa. Se estamos usando o custo quadrático que irá desacelerar a aprendizagem, ele não vai parar de aprender completamente, já que os pesos continuarão aprendendo com outras entradas de treinamento, mas é obviamente indesejável.
Construir aplicações de IA é uma habilidade com demanda cada vez maior no mercado.
Pensando nisso, a Data Science Academy oferece um programa completo, onde esses e vários outros conceitos são estudados em detalhes e com várias aplicações práticas, usando PyTorch. A Formação Engenheiro de IA é composta de 6 cursos, tudo 100% online e 100% em português, que aliam teoria e prática na medida certa, com aplicações reais de Inteligência Artificial. Confira o programa completo dos cursos: Formação Engenheiro de IA. Várias empresas em todo Brasil já estão treinando seus profissionais conosco! Venha fazer parte da revolução da IA.
Até o próximo capítulo!
Referências:
Neural Networks & The Backpropagation Algorithm, Explained
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning
Pattern Recognition and Machine Learning

