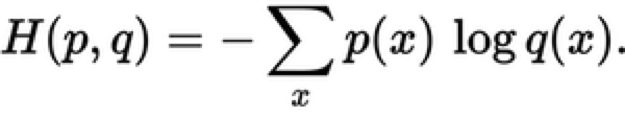Capítulo 18 – Entropia Cruzada Para Quantificar a Diferença Entre Duas Distribuições de Probabilidade
A Cross-Entropy (ou entropia cruzada, se você preferir o termo em português) é fácil de implementar como parte de um programa que aprende usando gradiente descendente e backpropagation. Faremos isso nos próximos capítulos quando treinarmos uma rede completa, desenvolvendo uma versão melhorada do nosso programa anterior para classificar os dígitos manuscritos do dataset MNIST. O novo programa é chamado de network2.py e incorpora não apenas a entropia cruzada, mas também várias outras técnicas que estudaremos mais adiante. Agora, vejamos como usar a Entropia Cruzada Para Quantificar a Diferença Entre Duas Distribuições de Probabilidade.
Por enquanto, vamos ver como nosso novo programa classifica os dígitos MNIST. Usaremos uma rede com 30 neurônios ocultos, e usaremos um tamanho de mini-lote de 10. Definimos a taxa de aprendizado para η = 0,5 e nós treinamos por 30 épocas. A interface para o network2.py será um pouco diferente do network.py, mas ainda deve estar claro o que está acontecendo. Nos próximos capítulos apresentamos o código completo disponível aqui.
Perceba que o comando net.large_weight_initializer() é usado para inicializar os pesos e vieses da mesma maneira que já descrevemos anteriormente. Precisamos executar este comando porque mais adiante vamos alterar o peso padrão para inicialização em nossas redes. O resultado da execução da sequência de comandos acima é uma rede com 95,49% de precisão.
Vejamos também o caso em que usamos 100 neurônios ocultos, a entropia cruzada, e mantemos os parâmetros da mesma forma. Neste caso, obtemos uma precisão de 96,82%. Essa é uma melhoria substancial em relação aos resultados que obtivemos nos capítulos anteriores, onde a precisão de classificação foi de 96,59%, usando o custo quadrático. Isso pode parecer uma pequena mudança, mas considere que a taxa de erro caiu de 3,41% para 3,18%. Ou seja, eliminamos cerca de um em quatorze dos erros originais. Isso é uma melhoria bastante útil.
É encorajador que o custo de entropia cruzada nos dê resultados semelhantes ou melhores do que o custo quadrático. No entanto, esses resultados não provam conclusivamente que a entropia cruzada é uma escolha melhor. A razão é que nós colocamos apenas um pequeno esforço na escolha de hyperparâmetros como taxa de aprendizado, tamanho de mini-lote e assim por diante. Para que a melhoria seja realmente convincente, precisaríamos fazer um trabalho completo de otimização desses hyperparâmetros. Ainda assim, os resultados são encorajadores e reforçam nosso argumento teórico anterior de que a entropia cruzada é uma escolha melhor do que o custo quadrático.
Isso, a propósito, é parte de um padrão geral que veremos nos próximos capítulos e, na verdade, em grande parte do restante do livro. Vamos desenvolver uma nova técnica, vamos experimentá-la e obteremos resultados “aprimorados”. É claro que é bom vermos essas melhorias, mas a interpretação de tais melhorias é sempre problemática. Elas só são verdadeiramente convincentes se virmos uma melhoria depois de nos esforçarmos para otimizar todos os outros hyperparâmetros. Isso é uma grande quantidade de trabalho, exigindo muito poder de computação, e normalmente não vamos fazer uma investigação tão exaustiva. Em vez disso, procederemos com base em testes informais como os realizados até aqui.
Até agora, discutimos a entropia cruzada de forma bem detalhada. Por que tanto esforço quando a entropia cruzada nos dá apenas uma pequena melhora em nossos resultados com o dataset MNIST? Mais adiante veremos outras técnicas, notadamente a regularização, que trazem melhorias muito maiores. Então, por que tanto foco na entropia cruzada? Parte da razão é que a entropia cruzada é uma função de custo amplamente utilizada e, portanto, vale a pena compreendê-la bem. Mas a razão mais importante é que a saturação dos neurônios é um problema importante nas redes neurais, um problema ao qual voltaremos repetidamente ao longo do livro. Por isso discutimos a entropia cruzada em extensão pois é um bom laboratório para começar a entender a saturação dos neurônios e como ela pode ser abordada.
O que significa a entropia cruzada? De onde isso vem?
Nossa discussão sobre a entropia cruzada se concentrou na análise algébrica e na implementação prática. Isso é útil, mas deixa questões conceituais mais amplas não respondidas, como: o que significa a entropia cruzada? Existe alguma maneira intuitiva de pensar sobre a entropia cruzada? E quanto ao significado intuitivo da entropia cruzada? Como devemos pensar sobre isso?
Explicar isso em profundidade nos levaria mais longe do que queremos ir neste livro. No entanto, vale ressaltar que existe uma maneira padrão de interpretar a entropia cruzada que vem do campo da teoria da informação. Vejamos.
Já sabemos que para treinar uma rede neural, você precisa encontrar o erro entre as saídas calculadas e as saídas alvo desejadas. A medida de erro mais comum é chamada de erro quadrático médio (ou Mean Square Error). No entanto, existem alguns resultados de pesquisa que sugerem o uso de uma medida diferente, denominada erro de entropia cruzada, como método preferível em relação ao erro quadrático médio.
A medida de entropia cruzada tem sido utilizada como alternativa ao erro quadrático médio. A entropia cruzada pode ser usada como uma medida de erro quando as saídas de uma rede podem ser pensadas como representando hipóteses independentes (por exemplo, cada nó significa um conceito diferente) e as ativações dos nós podem ser entendidas como representando a probabilidade (ou a confiança) que cada uma das hipóteses pode ser verdadeira. Nesse caso, o vetor de saída representa uma distribuição de probabilidade, e nossa medida de erro – entropia cruzada – indica a distância entre o que a rede acredita que essa distribuição deve ser e o que realmente deveria ser. Existe também uma razão prática para usar a entropia cruzada. Pode ser mais útil em problemas nos quais os alvos são 0 e 1. A entropia cruzada tende a permitir que erros alterem pesos mesmo quando houver nós saturados (o que significa que suas derivadas são próximas de 0). Vamos compreender melhor isso:
A entropia cruzada é comumente usada para quantificar a diferença entre duas distribuições de probabilidade. Geralmente, a distribuição “verdadeira” (dos dados usados para treinamento) é expressa em termos de uma distribuição One-Hot.
Por exemplo, suponha que para uma instância de treinamento específica (uma única linha no seu dataset), a classe seja B (de 3 possíveis possibilidades: A, B e C). A distribuição única para esta instância de treinamento é, portanto:
Pr(Class A) Pr(Class B) Pr(Class C)
0.0 1.0 0.0
Você pode interpretar a distribuição acima da seguinte forma: a instância de treinamento tem 0% de probabilidade de ser classe A, 100% de probabilidade de ser classe B e 0% de probabilidade de ser a classe C.
Agora, suponha que seu algoritmo de aprendizado de máquina tenha previsto a seguinte distribuição de probabilidade:
Pr(Class A) Pr(Class B) Pr(Class C)
0.228 0.619 0.153
Quão próxima é a distribuição prevista da distribuição verdadeira? É isso que determina o erro de entropia cruzada. A entropia cruzada é representada por esta fórmula:
A soma é sobre as três classes A, B e C. Se você completar o cálculo, você achará que a perda é 0.479. Então, é assim que “longe” está a sua previsão da distribuição verdadeira.
A entropia cruzada é uma das muitas funções de perda possíveis. Essas funções de perda são tipicamente escritas como J(theta) e podem ser usadas dentro da descida do gradiente, que é uma estrutura iterativa para mover os parâmetros (ou coeficientes) para os valores ótimos. A entropia cruzada descreve a perda entre duas distribuições de probabilidade.
Ao usar uma rede neural para realizar classificação e predição, geralmente é melhor usar o erro de entropia cruzada do que o erro de classificação e um pouco melhor usar o erro de entropia cruzada do que o erro quadrático médio para avaliar a qualidade da rede neural. É importante deixar claro que estamos lidando apenas com uma rede neural que é usada para classificar os dados, como a previsão da concessão de crédito (sim ou não), ou ainda outras classificações como idade, sexo ou dígitos no dataset MNIST e assim por diante. Não estamos lidando com uma rede neural que faz regressão, onde o valor a ser previsto é numérico.
Até o próximo capítulo!
Referências:
Neural Networks & The Backpropagation Algorithm, Explained
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning
Pattern Recognition and Machine Learning