Capítulo 20 – Overfitting e Regularização – Parte 2
Aumentar a quantidade de dados de treinamento é uma maneira de reduzir o overfitting. Mas existem outras maneiras de reduzir a extensão de ocorrência do overfitting? Uma abordagem possível é reduzir o tamanho da nossa rede. No entanto, redes grandes têm o potencial de serem mais poderosas do que redes pequenas e essa é uma opção que só adotaríamos com relutância.
Felizmente, existem outras técnicas que podem reduzir o overfitting, mesmo quando temos uma rede de tamanho fixo e dados de treinamento em quantidade limitada. Essas técnicas são conhecidos como técnicas de regularização. Neste capítulo descrevemos uma das técnicas de regularização mais comumente usadas, uma técnica às vezes conhecida como decaimento de peso (weight decay) ou Regularização L2. A ideia da Regularização L2 é adicionar um termo extra à função de custo, um termo chamado termo de regularização. Aqui está a entropia cruzada regularizada:
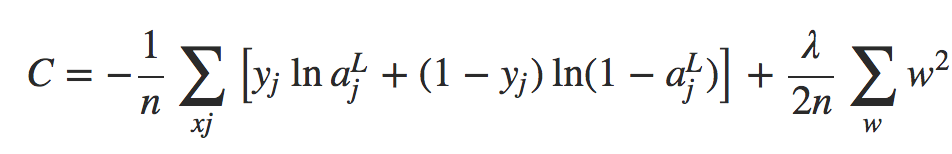
Equação 1
O primeiro termo é apenas a expressão usual para a entropia cruzada. Mas adicionamos um segundo termo, a soma dos quadrados de todos os pesos da rede. Isto é escalonado por um fator λ / 2n, onde λ > 0 é conhecido como o parâmetro de regularização e n é, como de costume, o tamanho do nosso conjunto de treinamento. Vou discutir mais tarde como λ é escolhido. É importante notar também que o termo de regularização não inclui os vieses. Eu também voltarei a isso mais frente.
Claro, é possível regularizar outras funções de custo, como o custo quadrático. Isso pode ser feito de maneira semelhante:
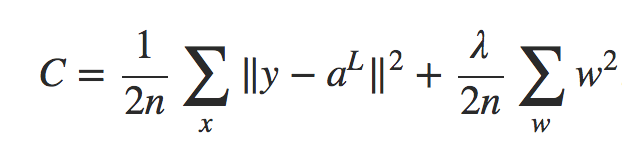
Equação 2
Em ambos os casos, podemos escrever a função de custo regularizada como:
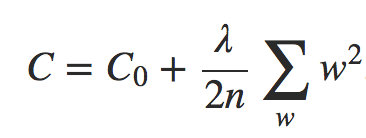
Equação 3
onde C0 é a função de custo original e não regularizada.
Intuitivamente, o efeito da regularização é fazer com que a rede prefira aprender pequenos pesos, sendo todas as outras coisas iguais. Pesos grandes só serão permitidos se melhorarem consideravelmente a primeira parte da função de custo. Dito de outra forma, a regularização pode ser vista como uma forma de se comprometer entre encontrar pequenos pesos e minimizar a função de custo original. A importância relativa dos dois elementos do compromisso depende do valor de λ: quando λ é pequeno, preferimos minimizar a função de custo original, mas quando λ é grande, preferimos pesos pequenos.
Agora, não é de todo óbvio porque fazer este tipo de compromisso deve ajudar a reduzir o overfitting! Mas acontece que sim, reduz. Abordaremos a questão de porque isso ajuda na redução do overfitting no próximo capítulo, mas primeiro vamos trabalhar em um exemplo mostrando como a regularização reduz o overfitting.
Para construir um exemplo, primeiro precisamos descobrir como aplicar nosso algoritmo de aprendizado de descida de gradiente estocástico em uma rede neural regularizada. Em particular, precisamos saber como calcular as derivadas parciais ∂C/∂w e ∂C/∂b para todos os pesos e vieses na rede. Tomando as derivadas parciais da Equação 3 acima, temos:
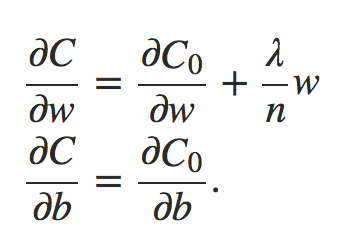
Equação 4
Os termos ∂C0/∂w e ∂C0/∂b podem ser calculados usando backpropagation, conforme descrito nos capítulos anteriores. E assim vemos que é fácil calcular o gradiente da função de custo regularizada, pois basta usar backpropagation, como de costume, e depois adicionar (λ/n).w à derivada parcial de todos os termos de peso. As derivadas parciais em relação aos vieses são inalteradas e, portanto, a regra de aprendizado de descida de gradiente para os vieses não muda da regra usual:
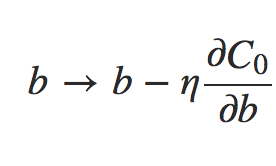
Equação 5
A regra de aprendizado para os pesos se torna:
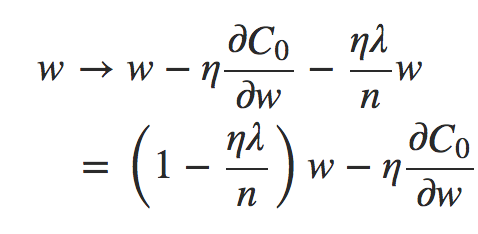
Equação 6
Isto é exatamente o mesmo que a regra usual de aprendizado de descida de gradiente, exceto pelo fato de primeiro redimensionarmos o peso w por um fator 1 − (ηλ/n). Esse reescalonamento é, às vezes, chamado de redução de peso, uma vez que diminui os pesos. À primeira vista, parece que isso significa que os pesos estão sendo direcionados para zero, mas isso não é bem isso, uma vez que o outro termo pode levar os pesos a aumentar, se isso causar uma diminuição na função de custo não regularizada.
Ok, é assim que a descida de gradiente funciona. E quanto à descida de gradiente estocástica? Bem, assim como na descida de gradiente estocástica não-regularizada, podemos estimar ∂C0/∂w pela média de um mini-lote de m exemplos de treinamento. Assim, a regra de aprendizagem regularizada para a descida de gradiente estocástica torna-se:
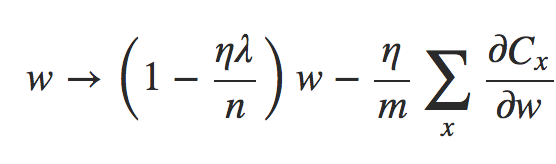
Equação 7
onde a soma é sobre exemplos de treinamento x no mini-lote, e Cx é o custo (não-regularizado) para cada exemplo de treinamento. Isto é exatamente o mesmo que a regra usual para descida de gradiente estocástico, exceto pelo fator de decaimento de peso de 1 − (ηλ/n). Finalmente, e por completo, deixe-me declarar a regra de aprendizagem regularizada para os vieses. Isto é, naturalmente, exatamente o mesmo que no caso não regularizado:
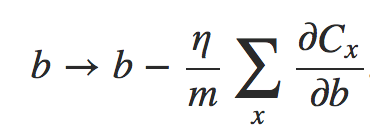
Equação 8
onde a soma é sobre exemplos de treinamento x no mini-lote.
Vamos ver como a regularização altera o desempenho da nossa rede neural. Usaremos uma rede com 30 neurônios ocultos, um tamanho de mini-lote de 10, uma taxa de aprendizado de 0,5 e a função de custo de entropia cruzada. No entanto, desta vez vamos usar um parâmetro de regularização de λ = 0,1. Note que no código, usamos o nome da variável lmbda, porque lambda é uma palavra reservada em Python, com um significado não relacionado ao que estamos fazendo aqui (caso tenha dúvidas sobre as palavras reservadas em Python, acesse o curso gratuito de Python em nosso portal).
Eu também usei o test_data novamente, não o validation_data. Estritamente falando, devemos usar o validation_data, por todas as razões que discutimos anteriormente. Mas decidi usar o test_data porque ele torna os resultados mais diretamente comparáveis com nossos resultados anteriores e não regularizados. Você pode facilmente alterar o código para usar o validation_data e você verá que ele terá resultados semelhantes.

O custo com os dados de treinamento diminui durante todo o tempo, da mesma forma que no caso anterior, não regularizado no capítulo anterior:
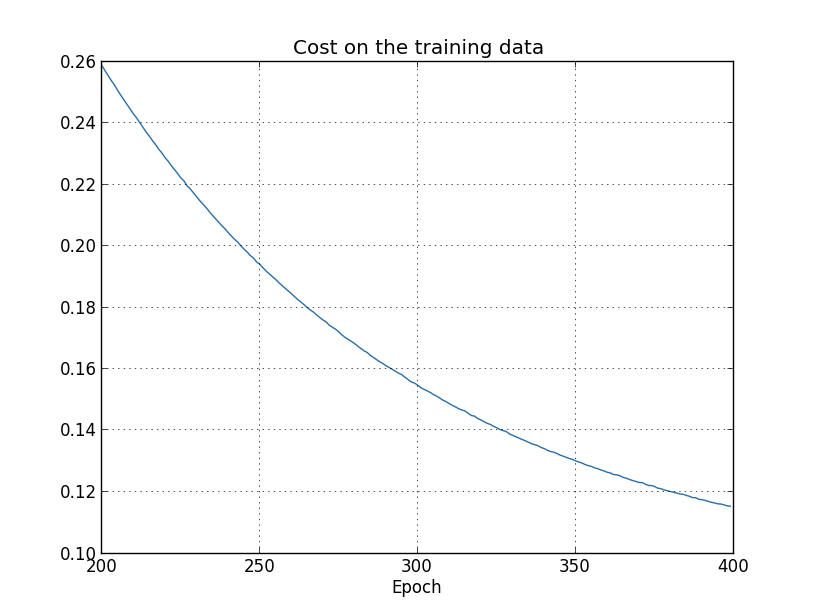
Mas desta vez a precisão no test_data continua a aumentar durante as 400 épocas:
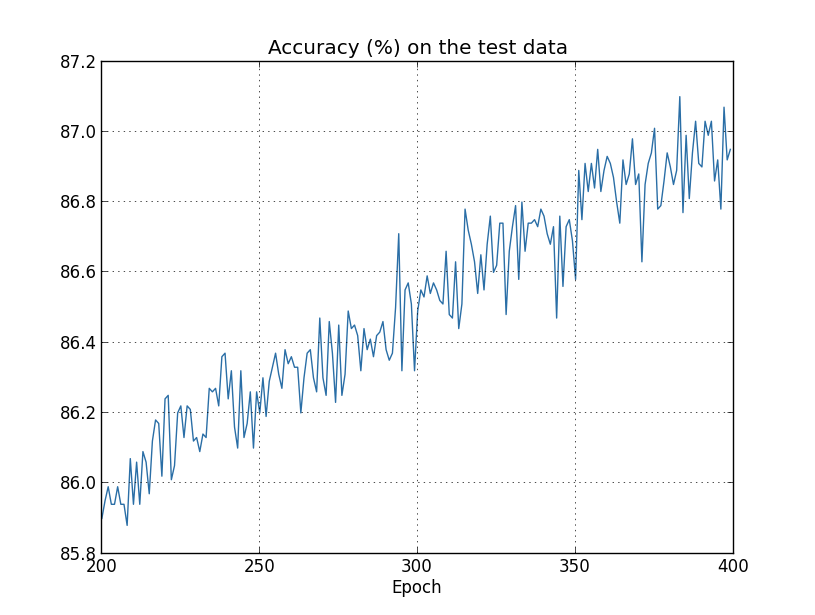
Claramente, o uso da regularização suprimiu o overfitting. Além do mais, a precisão é consideravelmente maior, com uma precisão de classificação de pico de 87.1%, em comparação com o pico de 82.27% obtido no caso não regularizado. De fato, quase certamente poderíamos obter resultados consideravelmente melhores, continuando a treinar mais de 400 épocas. Parece que, empiricamente, a regularização está fazendo com que nossa rede generalize melhor e reduza consideravelmente os efeitos do overfitting.
O que acontece se sairmos do ambiente artificial de ter apenas 1.000 imagens de treinamento e retornar ao conjunto completo de treinamento de 50.000 imagens? É claro, já vimos que o overfitting é muito menos problemático com as 50.000 imagens. A regularização ajuda ainda mais? Vamos manter os hiperparâmetros iguais ao exemplo anterior – 30 épocas, taxa de aprendizado de 0,5, tamanho de mini-lote de 10. No entanto, precisamos modificar o parâmetro de regularização. A razão é porque o tamanho n do conjunto de treinamento mudou de n = 1.000 para n = 50.000, e isso muda o fator de decaimento de peso 1 − (ηλ/n). Se continuássemos a usar λ = 0,1, isso significaria muito menos perda de peso e, portanto, muito menos efeito de regularização. Nós compensamos mudando para λ = 5.0.
Ok, vamos treinar nossa rede, parando primeiro para reinicializar os pesos:

Obtemos os resultados:
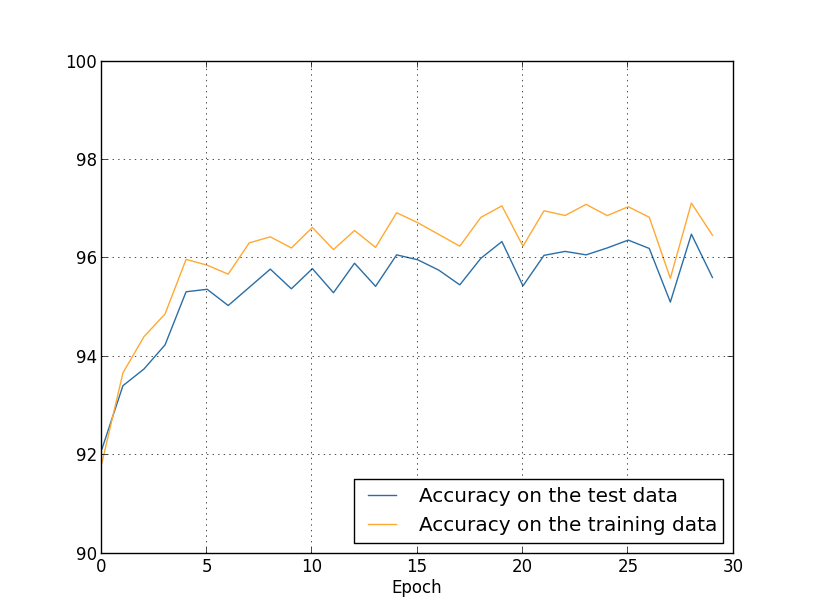
Há muitas boas notícias aqui. Primeiro, nossa precisão de classificação nos dados de teste aumentou de 95.49%, quando não foi regularizada, para 96.49%. Isso é uma grande melhoria. Em segundo lugar, podemos ver que a diferença entre os resultados nos dados de treinamento e teste é muito menor do que antes, com um percentual abaixo de zero. Essa ainda é uma lacuna significativa, mas obviamente fizemos um progresso substancial para reduzir o overfitting.
Finalmente, vamos ver qual a precisão da classificação de teste que obtemos quando usamos 100 neurônios ocultos e um parâmetro de regularização de λ = 5.0. Eu não vou passar por uma análise detalhada de overfitting aqui, isso é puramente por diversão, só para ver a precisão que podemos obter quando usamos nossos novos truques: a função de custo de entropia cruzada e a Regularização L2.

O resultado final é uma precisão de classificação de 97.92% nos dados de validação. É um grande salto do caso dos 30 neurônios ocultos. Na verdade, ajustando um pouco mais, para executar por 60 épocas com η = 0.1 e λ = 5.0, quebramos a barreira de 98%, alcançando uma precisão de classificação de 98.04% nos dados de validação. Nada mal para o que acaba sendo 152 linhas de código!
Descrevi a regularização como uma forma de reduzir o overfitting e aumentar as precisões de classificação. Na verdade, esse não é o único benefício. Empiricamente, ao executar várias execuções de nossas redes com o dataset MNIST, mas com diferentes inicializações de peso (aleatórias), descobrimos que as execuções não-regularizadas ocasionalmente ficarão “presas”, aparentemente capturadas em mínimos locais da função de custo. O resultado é que diferentes execuções às vezes fornecem resultados bastante diferentes. Por outro lado, as execuções regularizadas forneceram resultados muito mais facilmente replicáveis.
Por que isso está acontecendo? Heuristicamente, se a função de custo for desregularizada, o comprimento do vetor de peso provavelmente crescerá, todas as outras coisas sendo iguais. Com o tempo, isso pode levar o vetor de peso a ser realmente muito grande. Isso pode fazer com que o vetor de peso fique preso apontando mais ou menos na mesma direção, já que as mudanças devido a descida do gradiente fazem apenas pequenas alterações na direção, quando o comprimento é longo. Acredito que esse fenômeno esteja dificultando o nosso algoritmo de aprendizado para explorar adequadamente o espaço de pesos e, consequentemente, mais difícil encontrar bons mínimos da função de custo.
Ainda não acabamos sobre regularização. Mais sobre isso no próximo capítulo! Até lá!
Referências:
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning
Pattern Recognition and Machine Learning

