Capítulo 25 – Inicialização de Pesos em Redes Neurais Artificiais
Quando criamos nossas redes neurais, temos que fazer escolhas para os valores iniciais de pesos e vieses (bias). Até agora, nós os escolhemos de acordo com uma prescrição que discutimos nos capítulos anteriores.
Só para lembrar, a prescrição era escolher tanto os pesos quanto os vieses usando variáveis aleatórias Gaussianas independentes, normalizadas para ter a média 0 e desvio padrão 1 (esse é um conceito fundamental em Estatística e caso queira adquirir conhecimento em Estatística na prática através de projetos, acesse aqui: Formação Análise Estatística.
Embora esta abordagem tenha funcionado bem, foi bastante ad-hoc, e vale a pena revisitar para ver se podemos encontrar uma maneira melhor de definir nossos pesos e vieses iniciais, e talvez ajudar nossas redes neurais a aprender mais rápido. É o que iremos estudar neste capítulo.
Para começar, vamos compreender porque podemos fazer um pouco melhor do que inicializar pesos e vieses com valores Gaussianos normalizados. Para ver porque, suponha que estamos trabalhando com uma rede com um grande número – digamos 1.000 – de neurônios de entrada. E vamos supor que usamos valores Gaussianos normalizados para inicializar os pesos conectados à primeira camada oculta. Por enquanto, vou me concentrar especificamente nos pesos que conectam os neurônios de entrada ao primeiro neurônio na camada oculta e ignorar o restante da rede:
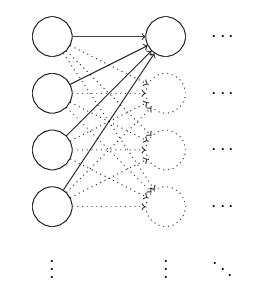
Vamos supor, por simplicidade, que estamos tentando treinar usando uma entrada de treinamento x na qual metade dos neurônios de entrada estão ativados, isto é, configurados para 1, e metade dos neurônios de entrada estão desligados, ou seja, ajustados para 0. O argumento a seguir aplica-se de forma mais geral, mas você obterá a essência deste caso especial. Vamos considerar a soma ponderada z = ∑jwjxj + b de entradas para nosso neurônio oculto. Ocorre que 500 termos nesta soma desaparecem, porque a entrada correspondente xj é zero e, assim, z é uma soma sobre um total de 501 variáveis aleatórias Gaussianas normalizadas, representando os 500 termos de peso e o termo extra de viés (bias). Logo, z é ele próprio uma distribuição Gaussiana com média zero e desvio padrão ≈ 22.4 (raiz quadrada de 501). Ou seja, z tem uma distribuição Gaussiana muito ampla, sem um pico agudo, conforme a figura abaixo:
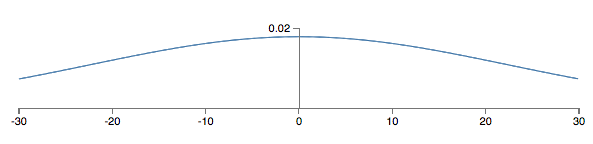
Em particular, podemos ver neste gráfico que é bem provável que | z | será bastante grande, isto é, z > 1 ou z < -1. Se for esse o caso, a saída σ(z) do neurônio oculto estará muito próxima de 1 ou 0. Isso significa que nosso neurônio oculto terá saturado. E quando isso acontece, como sabemos, fazer pequenas mudanças nos pesos fará apenas mudanças absolutamente minúsculas na ativação de nosso neurônio oculto. Essa mudança minúscula na ativação do neurônio oculto, por sua vez, dificilmente afetará o resto dos neurônios na rede, e veremos uma mudança minúscula correspondente na função de custo.
Como resultado, esses pesos só aprenderão muito lentamente quando usarmos o algoritmo de descida do gradiente. É semelhante ao problema que discutimos anteriormente em outros capítulos, no qual os neurônios de saída que saturaram o valor errado fizeram com que o aprendizado diminuísse. Abordamos esse problema anterior com uma escolha inteligente de função de custo. Infelizmente, enquanto isso ajudou com os neurônios de saída saturados, ele não faz nada pelo problema dos neurônios ocultos saturados.
Temos falado sobre a entrada de pesos para a primeira camada oculta. Naturalmente, argumentos semelhantes aplicam-se também a camadas ocultas posteriores: se os pesos em camadas ocultas posteriores forem inicializados usando Gaussianos normalizados, então as ativações estarão frequentemente muito próximas de 0 ou 1, e o aprendizado prosseguirá muito lentamente.
Existe alguma maneira de escolhermos melhores inicializações para os pesos e vieses, para que não tenhamos esse tipo de saturação e, assim, evitar uma desaceleração na aprendizagem? Suponha que tenhamos um neurônio com pesos de entrada nin. Então, inicializaremos esses pesos como variáveis aleatórias gaussianas com média 0 e desvio padrão:
![]()
Isto é, vamos “esmagar os gaussianos”, tornando menos provável que nosso neurônio seja saturado. Continuaremos a escolher o viés como um Gaussiano com média 0 e desvio padrão 1, por motivos pelos quais voltaremos daqui a pouco. Com essas escolhas, a soma ponderada z = ∑jwjxj + b será novamente uma variável aleatória Gaussiana com média 0, mas será muito mais aguda que antes. Suponha, como fizemos anteriormente, que 500 das entradas são zero e 500 são 1. Então é fácil mostrar (veja o gráfico abaixo) que z tem uma distribuição Gaussiana com média 0 e desvio padrão igual a 1,22…(raiz quadrada de 3/2). Isso é muito mais agudo do que antes, tanto que até o gráfico abaixo subestima a situação, já que precisamos redimensionar o eixo vertical, quando comparado ao gráfico anterior:
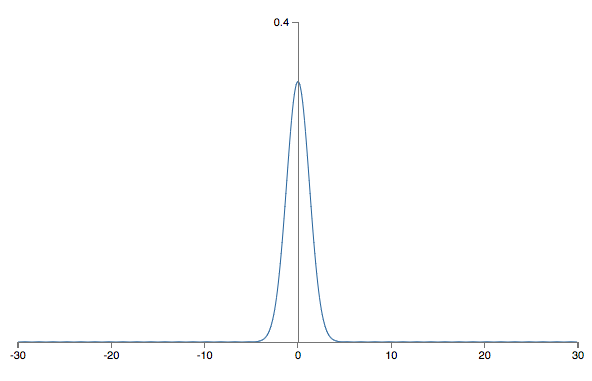
É muito menos provável que tal neurônio sature e, correspondentemente, é muito menos provável que tenha problemas com a lentidão do aprendizado.
Eu afirmei acima que nós continuaremos a inicializar os vieses como antes, como variáveis aleatórias Gaussianas com uma média de 0 e um desvio padrão de 1. Isto não tem problema, pois é pouco provável que nossos neurônios vão saturar. Na verdade, não importa muito como inicializamos os vieses, desde que evitemos o problema com a saturação dos neurônios. Algumas pessoas vão tão longe a ponto de inicializar todos os vieses com 0, e dependem da descida de gradiente para aprender vieses apropriados. Mas como é improvável que faça muita diferença, continuaremos com o mesmo procedimento de inicialização de antes.
Vamos comparar os resultados para as nossas abordagens antiga e nova para inicialização de peso, usando a tarefa de classificação de dígitos MNIST. Como antes, usaremos 30 neurônios ocultos, um tamanho de mini-lote de 10, um parâmetro de regularização λ = 5.0 e a função de custo de entropia cruzada. Diminuiremos ligeiramente a taxa de aprendizado de η = 0,5 para 0,1, pois isso torna os resultados um pouco mais visíveis nos gráficos. Podemos treinar usando o antigo método de inicialização de peso (você pode baixar os arquivos aqui):

Também podemos treinar usando a nova abordagem para inicializar o peso. Na verdade, isso é ainda mais fácil, já que a maneira padrão de inicializar os pesos da rede2 é usar essa nova abordagem. Isso significa que podemos omitir a chamada net.large_weight_initializer () acima:

Plotando os resultados, obtemos:
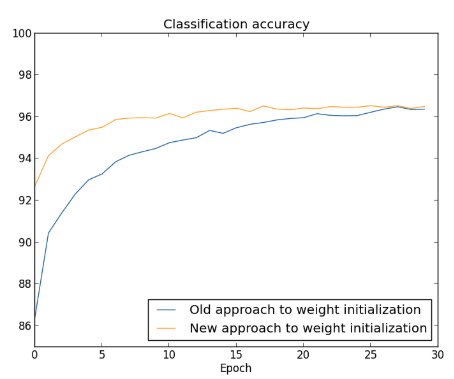
Em ambos os casos, acabamos com uma precisão de classificação um pouco acima de 96%. A precisão final da classificação é quase exatamente a mesma nos dois casos, mas a nova técnica de inicialização é muito, muito mais rápida. No final da primeira época de treinamento, a antiga abordagem de inicialização de peso tem uma precisão de classificação abaixo de 87%, enquanto a nova abordagem já chega a quase 93%. O que parece estar acontecendo é que nossa nova abordagem para a inicialização do peso nos leva a um processo muito melhor, o que nos permite obter bons resultados muito mais rapidamente. O mesmo fenômeno também é visto se traçarmos resultados com 100 neurônios ocultos:
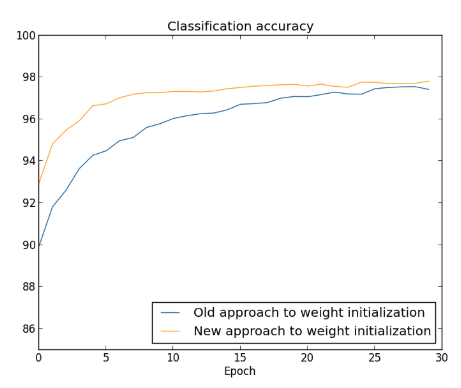
Neste caso, as duas curvas não se encontram. No entanto, nossas experiências sugerem que, com apenas mais algumas épocas de treinamento (não mostradas), as precisões se tornam quase exatamente as mesmas. Portanto, com base nesses experimentos, parece que a inicialização do peso aprimorado apenas acelera o aprendizado, não altera o desempenho final de nossas redes. No entanto, veremos mais a frente alguns exemplos de redes neurais em que o comportamento de longo prazo é significativamente melhor com a inicialização de peso usando:
![]()
Assim, não é apenas a velocidade de aprendizado que é melhorada, mas também o desempenho final.
A abordagem acima para a inicialização do peso ajuda a melhorar a maneira como nossas redes neurais aprendem. Outras técnicas para inicialização de peso também foram propostas, muitas baseadas nessa ideia básica. Não vamos rever as outras abordagens aqui, já que a descrita anteriormente funciona bem o suficiente para nossos propósitos. Se você estiver interessado em pesquisar mais, recomendamos a leitura das páginas 14 e 15 de um artigo de 2012 de Yoshua Bengio (um dos padrinhos do Deep Learning), bem como as referências nele contidas: Practical Recommendations for Gradient-Based Training of Deep Architectures.
Para aplicar esses conceitos na prática com Linguagem Python, acesse aqui: Deep Learning Para Aplicações de IA com PyTorch e Lightning
Até o próximo capítulo!
Referências:
Formação Engenheiro de Machine Learning
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning

