Capítulo 26 – Como Escolher os Hiperparâmetros de Uma Rede Neural
Até agora não explicamos como foram escolhidos os valores dos hiperparâmetros como a taxa de aprendizado, η, o parâmetro de regularização, λ e assim por diante. Fornecemos valores que funcionaram muito bem, mas, na prática, quando você está usando redes neurais para resolver um problema, pode ser difícil encontrar bons parâmetros. Neste capítulo, começamos nosso estudo sobre Como Escolher os Hiperparâmetros de Uma Rede Neural. Vamos começar?
Imagine, por exemplo, que acabamos de ser apresentados ao dataset MNIST e começamos a trabalhar nele, sem saber nada sobre quais hiperparâmetros usar. Vamos supor que, por sorte, em nossos primeiros experimentos, escolhemos muitos dos hiperparâmetros da mesma forma como foi feito nos capítulos anteriores: 30 neurônios ocultos, um tamanho de mini-lote de 10, treinando por 30 épocas usando a entropia cruzada. Mas escolhemos uma taxa de aprendizado η = 10.0 e o parâmetro de regularização λ = 1000.0. Aqui está um exemplo de execução da rede (o script está disponível aqui):
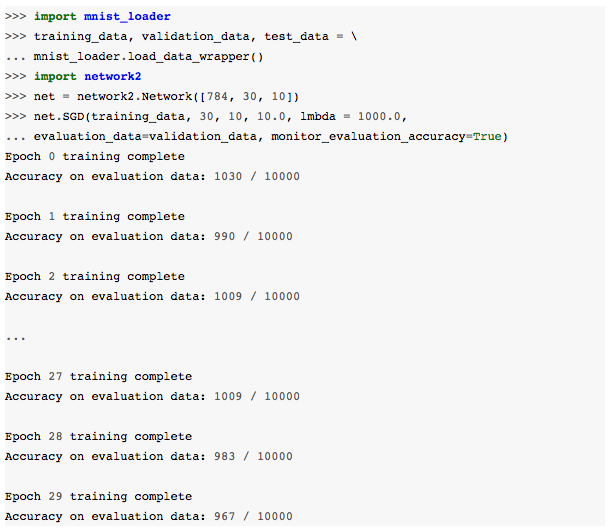
Nossas precisões de classificação não são melhores do que o acaso! Nossa rede está agindo como um gerador de ruído aleatório!
“Bem, isso é fácil de consertar”, você pode dizer, “apenas diminua a taxa de aprendizado e os hiperparâmetros de regularização”. Infelizmente, você não sabe a priori quais são os hiperparâmetros que você precisa ajustar. Talvez o verdadeiro problema seja que nossa rede de neurônios ocultos nunca funcionará bem, não importa como os outros hiperparâmetros sejam escolhidos? Talvez realmente precisemos de pelo menos 100 neurônios ocultos? Ou 300 neurônios ocultos? Ou várias camadas ocultas? Ou uma abordagem diferente para codificar a saída? Talvez nossa rede esteja aprendendo, mas precisamos treinar em mais épocas? Talvez os mini-lotes sejam pequenos demais? Talvez seja melhor voltarmos para a função de custo quadrático? Talvez precisemos tentar uma abordagem diferente para inicializar o peso? E assim por diante. Se fosse fácil, não precisaríamos de um Cientista de Dados, não é verdade?
É fácil sentir-se perdido com tantas escolhas e combinações possíveis para os hiperparâmetros. Isso pode ser particularmente frustrante se sua rede for muito grande ou usar muitos dados de treinamento, pois você pode treinar por horas, dias ou semanas, apenas para não obter resultados. Se a situação persistir, prejudicará sua confiança. Talvez as redes neurais sejam a abordagem errada para o seu problema? Talvez você devesse largar o emprego e trabalhar com a apicultura?
Nos próximos capítulos, explicaremos algumas heurísticas que podem ser usadas para definir os hiperparâmetros em uma rede neural. O objetivo é ajudá-lo a desenvolver um fluxo que permita que você faça um bom trabalho definindo hiperparâmetros. Claro, não vamos cobrir tudo sobre otimização de hiperparâmetros. Esse é um assunto enorme, e não é, de qualquer forma, um problema que já está completamente resolvido, nem existe um acordo universal entre os profissionais sobre as estratégias corretas a serem usadas. Há sempre mais um truque que você pode tentar para obter um pouco mais de desempenho da sua rede. Mas temos algumas heurísticas com as quais podemos começar.
Compreendendo a Situação – Estratégia Geral
Ao usar redes neurais para atacar um novo problema, o primeiro desafio é obter qualquer aprendizado não-trivial, ou seja, para que a rede obtenha resultados melhores que o acaso. Isso pode ser surpreendentemente difícil, especialmente ao confrontar uma nova classe de problemas. Vejamos algumas estratégias que você pode usar se tiver esse tipo de problema.
Suponha, por exemplo, que você esteja atacando o MNIST pela primeira vez. Você começa entusiasmado, mas fica um pouco desanimado quando sua primeira rede falha completamente, como no exemplo acima. O caminho a percorrer é reduzir o tamanho do problema. Livre-se de todas as imagens de treinamento e validação, exceto imagens de 0s ou 1s. Em seguida, tente treinar uma rede para distinguir 0s de 1s. Não só isso é um problema inerentemente mais fácil do que distinguir todos os dez dígitos, como também reduz a quantidade de dados de treinamento em 80%, acelerando o treinamento por um fator de 5. Isso permite experimentações muito mais rápidas e, portanto, fornece uma visão mais rápida sobre como construir uma boa rede.
Você pode acelerar ainda mais a experimentação, desmembrando sua rede na rede mais simples, provavelmente fazendo aprendizado significativo. Se você acredita que uma rede [784, 10] provavelmente faz uma classificação melhor que o acaso com o dataset de dígitos MNIST, então comece sua experimentação com essa rede. Vai ser muito mais rápido do que treinar uma rede [784, 30, 10], e você pode “falhar” mais rápido (este é um conceito muito comum nos EUA: “fail fast”, ou seja, cometa falhas o mais rápido possível e aprenda com elas. Não se preocupe em tentar atingir a perfeição, pois você não vai conseguir de qualquer forma).
Você pode acelerar mais na experimentação aumentando a frequência de monitoramento. No network2.py, monitoramos o desempenho no final de cada época de treinamento. Com 50.000 imagens por época, isso significa esperar um pouco – cerca de dez segundos por época, no meu laptop, ao treinar uma rede [784, 30, 10] – antes de obter feedback sobre o quanto a rede está aprendendo.
É claro que dez segundos não são muito longos, mas se você quiser testar dezenas de opções de hiperparâmetros, é irritante, e se você quiser testar centenas ou milhares de opções, isso começa a ficar debilitante. Podemos obter feedback mais rapidamente, monitorando a precisão da validação com mais frequência, digamos, a cada 1.000 imagens de treinamento. Além disso, em vez de usar o conjunto completo de 10.000 imagens de validação para monitorar o desempenho, podemos obter uma estimativa muito mais rápida usando apenas 100 imagens de validação.
Tudo o que importa é que a rede veja imagens suficientes para aprender de verdade e obter uma boa estimativa aproximada de desempenho. Claro, nosso programa network2.py atualmente não faz esse tipo de monitoramento. Mas, como um clímax para obter um efeito semelhante para fins de ilustração, vamos reduzir nossos dados de treinamento para apenas as primeiras 1.000 imagens de treinamento MNIST. Vamos tentar e ver o que acontece. (Para manter o código abaixo simples, não implementei a ideia de usar apenas imagens 0 e 1. Claro, isso pode ser feito com um pouco mais de trabalho).
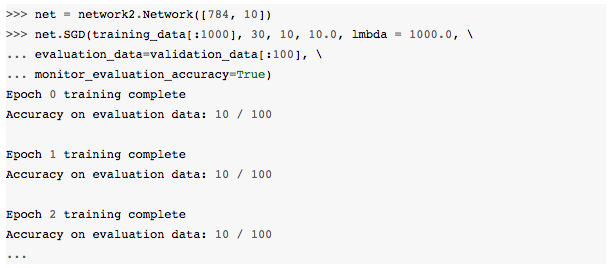
Ainda estamos recebendo puro ruído! Mas há uma grande vitória: agora estamos obtendo feedback em uma fração de segundo, em vez de uma vez a cada dez segundos. Isso significa que você pode experimentar mais rapidamente outras opções de hiperparâmetros, ou até mesmo conduzir experimentos testando muitas opções diferentes de hiperparâmetros quase simultaneamente.
No exemplo acima, eu deixamos λ como λ = 1000.0, como usamos anteriormente. Mas como mudamos o número de exemplos de treinamento, deveríamos realmente mudar λ para manter weight decay o mesmo. Isso significa mudar λ para 20.0. Se fizermos isso, então é o que acontece:

Ah! Nós temos um sinal. Não é um sinal muito bom, mas um sinal, no entanto. Isso é algo que podemos construir, modificando os hiperparâmetros para tentar melhorar ainda mais. Talvez nós achemos que nossa taxa de aprendizado precisa ser maior. (Como você talvez perceba, é um palpite bobo, por razões que discutiremos em breve, mas chegaremos lá. Não existe atalho para o aprendizado). Então, para testar nosso palpite, tentamos alterar η até 100.0:

Isso não é bom, pois sugere que nosso palpite estava errado e o problema não era que a taxa de aprendizado fosse muito baixa. Então, em vez disso, tentamos alterar η para η = 1.0:

Agora ficou melhor! E assim podemos continuar, ajustando individualmente cada hiperparâmetro, melhorando gradualmente o desempenho. Uma vez feita a exploração para encontrar um valor melhor para η, seguimos para encontrar um bom valor para λ. Em seguida, experimente uma arquitetura mais complexa, digamos uma rede com 10 neurônios ocultos e ajuste os valores para η e λ novamente. Depois, aumente para 20 neurônios ocultos e então, ajuste outros hiperparâmetros um pouco mais e assim por diante, em cada estágio avaliando o desempenho usando nossos dados de validação e usando essas avaliações para encontrar melhores hiperparâmetros. Ao fazer isso, normalmente leva mais tempo para testemunhar o impacto devido a modificações dos hiperparâmetros, e assim podemos diminuir gradualmente a frequência de monitoramento.
Tudo isso parece muito promissor como uma estratégia ampla. No entanto, quero voltar a esse estágio inicial de encontrar hiperparâmetros que permitem que uma rede aprenda qualquer coisa. De fato, mesmo a discussão acima transmite uma perspectiva muito positiva. Pode ser extremamente frustrante trabalhar com uma rede que não está aprendendo nada.
Você pode ajustar os hiperparâmetros por dias e ainda não obter uma resposta significativa. Por isso, gostaria de enfatizar novamente que, durante os primeiros estágios, você deve se certificar de que pode obter um feedback rápido dos experimentos. Intuitivamente, pode parecer que simplificar o problema e a arquitetura apenas irá atrasá-lo. Na verdade, isso acelera as coisas, pois você encontra muito mais rapidamente uma rede com um sinal significativo. Uma vez que você tenha recebido tal sinal, muitas vezes você pode obter melhorias rápidas aprimorando os hiperparâmetros. Assim como em tudo na vida, começar pode ser a coisa mais difícil a se fazer.
Ok, essa é a estratégia geral. Vamos agora olhar algumas recomendações específicas para definir hiperparâmetros. Vou me concentrar na taxa de aprendizado, η, no parâmetro de regularização L2, λ e no tamanho do mini-lote. No entanto, muitas das observações também se aplicam a outros hiperparâmetros, incluindo aqueles associados à arquitetura de rede, outras formas de regularização e alguns hiperparâmetros que encontraremos mais adiante aqui no Deep Learning Book, como o coeficiente momentum.
Oh não! O capítulo acabou! Fique tranquilo, continuamos no próximo. Até lá!
Referências:
Machine Learning Para Advogados
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

