Capítulo 27 – A Taxa de Aprendizado de Uma Rede Neural
Vamos continuar a discussão do capítulo anterior sobre a escolha dos hiperparâmetros de um modelo de rede neural, estudando um dos mais importantes, a taxa de aprendizado.
Suponha que executemos três redes neurais artificiais sendo treinadas com o dataset MNIST com três taxas de aprendizado diferentes, η = 0.025, η = 0.25 e η = 2.5, respectivamente. Vamos definir os outros hiperparâmetros de acordo com as experiências nos capítulos anteriores, executando mais de 30 epochs, com um tamanho de mini-lote de 10 e com λ = 5.0. Também voltaremos a usar todas as 50.000 imagens de treinamento. Aqui está um gráfico mostrando o comportamento do custo de treinamento enquanto treinamos:
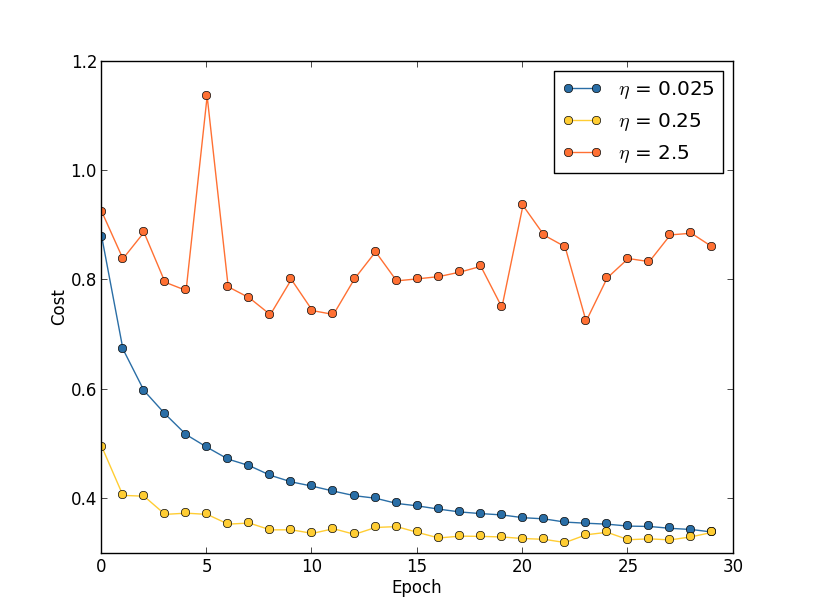
Com η = 0.025, o custo diminui suavemente até a época final. Com η = 0.25 o custo inicialmente diminui, mas após cerca de 20 épocas ele está próximo da saturação, e daí em diante a maioria das mudanças são meramente pequenas e aparentemente oscilações aleatórias. Finalmente, com η = 2.5, o custo faz grandes oscilações desde o início. Para entender o motivo das oscilações, lembre-se de que a descida estocástica do gradiente supostamente nos levará gradualmente a um vale da função de custo (conforme explicado aqui):
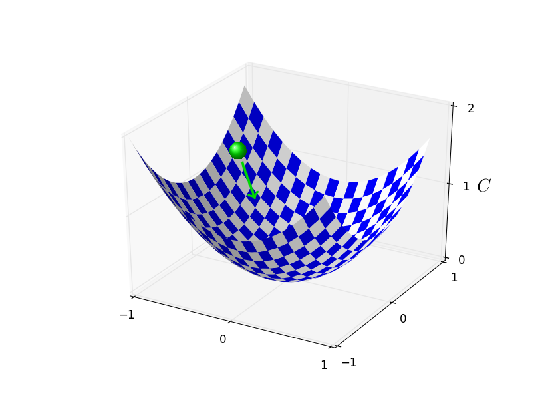
No entanto, se η for muito grande, os passos serão tão grandes que poderão, na verdade, ultrapassar o mínimo, fazendo com que o algoritmo simplesmente fique perdido durante o treinamento. Isso é provavelmente o que está causando a oscilação do custo quando η = 2.5. Quando escolhemos η = 0.25, os passos iniciais nos levam a um mínimo da função de custo, e é só quando chegamos perto desse mínimo que começamos a sofrer com o problema de overshooting. E quando escolhemos η = 0.025, não sofremos este problema durante as primeiras 30 épocas.
Claro, escolher η tão pequeno cria outro problema, que reduz a velocidade da descida estocástica do gradiente, aumentando o tempo total de treinamento. Uma abordagem ainda melhor seria começar com η = 0.25, treinar por 20 épocas e então mudar para η = 0.025. Discutiremos essas tabelas de taxas de aprendizado variáveis posteriormente. Por enquanto, porém, vamos nos ater a descobrir como encontrar um único valor bom para a taxa de aprendizado, η.
Com esta imagem em mente, podemos definir η da seguinte maneira. Primeiro, estimamos o valor limite para η no qual o custo nos dados de treinamento começa imediatamente a diminuir, em vez de oscilar ou aumentar. Essa estimativa não tem que ser muito precisa. Você pode estimar a ordem de magnitude começando com η = 0.01. Se o custo diminuir durante as primeiras épocas, então você deve sucessivamente tentar η = 0.1, 1.0,… até encontrar um valor para η onde o custo oscile ou aumente durante as primeiras poucas épocas (isso faz parte do trabalho de um Cientista de Dados).
Alternativamente, se o custo oscilar ou aumentar durante as primeiras épocas, quando η = 0.01, então tente η = 0.001 ,0.0001,… até encontrar um valor para η onde o custo diminui durante as primeiras poucas épocas. Seguindo este procedimento, obteremos uma estimativa da ordem de magnitude para o valor limite de η. Você pode, opcionalmente, refinar sua estimativa, para escolher o maior valor de η no qual o custo diminui durante as primeiras poucas épocas, digamos η = 0.5 ou η = 0.2 (não há necessidade de que isso seja super-preciso). Isso nos dá uma estimativa para o valor limite de η. E claro, documente tudo!!!!
Obviamente, o valor real de η que você usa não deve ser maior que o valor limite. De fato, se o valor de η permanecer utilizável ao longo de muitas épocas, então você provavelmente desejará usar um valor para η que seja menor, digamos, um fator de dois abaixo do limite. Essa escolha normalmente permitirá que você treine por muitas épocas, sem causar muita lentidão no aprendizado.
No caso dos dados MNIST, seguir esta estratégia leva a uma estimativa de 0.1 para a ordem de magnitude do valor limite de η. Depois de um pouco mais de refinamento, obtemos um valor limite η = 0.5. Seguindo a prescrição acima, isso sugere usar η = 0.25 como nosso valor para a taxa de aprendizado. De fato, eu descobri que usar η = 0.5 funcionava bem o suficiente em 30 épocas que, na maioria das vezes, eu não me preocupava em usar um valor menor de η.
Tudo isso parece bastante simples. No entanto, usar o custo de treinamento para escolher η parece contradizer o que dissemos anteriormente, que escolheríamos os hiperparâmetros avaliando o desempenho usando nossos dados de validação. Na verdade, usaremos a precisão de validação para escolher o hiperparâmetro de regularização, o tamanho do mini-lote e os parâmetros de rede, como o número de camadas e neurônios ocultos, e assim por diante (estudaremos isso nos próximos capítulos).
Por que as coisas diferem para a taxa de aprendizado? Francamente, essa escolha é uma preferência estética pessoal e talvez seja um tanto idiossincrática. O raciocínio é que os outros hiperparâmetros são destinados a melhorar a precisão final da classificação no conjunto de testes, e por isso faz sentido selecioná-los com base na precisão da validação. No entanto, a taxa de aprendizado é apenas para influenciar a precisão final da classificação. Sua finalidade principal é realmente controlar o tamanho da etapa na descida do gradiente e monitorar o custo do treinamento é a melhor maneira de detectar se o tamanho da etapa é muito grande. Com isso dito, essa é uma preferência pessoal. No início, durante o aprendizado, o custo do treinamento geralmente diminui apenas se a precisão da validação melhorar e assim, na prática, é improvável que faça muita diferença em qual critério você usa.
No próximo capítulo tem mais. Até lá!
Referências:
Machine Learning com Python e C++
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

