Capítulo 37 – O Efeito do Batch Size no Treinamento de Redes Neurais Artificiais
A partir deste capítulo você vai compreender em mais detalhes a arquitetura dos principais modelos de Deep Learning, com ênfase nas escolhas dos hiperparâmetros e abordagens de treinamento. Vamos começar com O Efeito do Batch Size no Treinamento de Redes Neurais Artificiais.
Neste experimento, vamos investigar o efeito do tamanho do lote (Batch Size) na dinâmica de treinamento. Tamanho do lote (Batch Size) é um termo usado em aprendizado de máquina e refere-se ao número de exemplos de treinamento usados em uma iteração. O Batch Size pode ser uma das três opções:
- batch mode: onde o tamanho do lote é igual ao conjunto de dados total, tornando os valores de iteração e épocas equivalentes.
- mini-batch mode: onde o tamanho do lote é maior que um, mas menor que o tamanho total do conjunto de dados. Geralmente, um número que pode ser dividido no tamanho total do conjunto de dados.
- stochastic mode: onde o tamanho do lote é igual a um. Portanto, o gradiente e os parâmetros da rede neural são atualizados após cada amostra.
A métrica em que nos concentraremos é o gap de generalização, que é definido como a diferença entre o valor do tempo de treinamento e o valor do tempo de teste. Vamos investigar o tamanho do lote no contexto da classificação de imagens (o mesmo usado em diversos capítulos anteriores). Especificamente, usaremos o conjunto de dados MNIST.
No nosso caso, a diferença de generalização é simplesmente a diferença entre a precisão da classificação no tempo de teste e o tempo de treinamento. Estas experiências foram destinadas a fornecer alguma intuição básica sobre os efeitos do tamanho do lote. É bem conhecido na comunidade de aprendizado de máquina que a dificuldade de fazer afirmações gerais sobre os efeitos de hiperparâmetros geralmente varia de conjunto de dados a conjunto de dados e modelo a modelo. Portanto, as conclusões que fazemos aqui só podem servir como indicações em vez de declarações gerais sobre o tamanho do lote.
O tamanho do lote é um dos hiperparâmetros mais importantes para sintonizar os modernos sistemas de aprendizagem profunda. Os Cientistas de Dados muitas vezes querem usar um tamanho de lote maior para treinar seu modelo, uma vez que permite acelerações computacionais do paralelismo das GPUs. No entanto, é bem conhecido que um tamanho de lote muito grande levará a uma generalização deficiente (embora atualmente não se saiba exatamente porque isso acontece). Para as funções convexas que estamos tentando otimizar, há uma disputa inerente entre os benefícios de tamanhos de lotes menores e maiores.
Por um lado, usar um lote igual a todo o conjunto de dados garante a convergência para o ótimo global da função objetivo. No entanto, isso é à custa de uma convergência empírica mais lenta para esse ótimo. Por outro lado, o uso de tamanhos menores de lotes mostrou empiricamente uma convergência mais rápida para soluções “boas”. Isso é intuitivamente explicado pelo fato de que tamanhos de lote menores permitem que o modelo “inicie o aprendizado antes de ver todos os dados”. A desvantagem de usar um tamanho de lote menor é que não há garantia que o modelo vai convergir para o ótimo global. Ele irá saltar em torno do ótimo global, dependendo da relação entre o tamanho do lote e o tamanho do conjunto de dados.
Portanto, sob nenhuma restrição computacional, muitas vezes é aconselhável que se comece com um pequeno tamanho de lote, colhendo os benefícios de uma dinâmica de treinamento mais rápida, e aumente o tamanho do lote por meio de treinamento, aproveitando também os benefícios da convergência garantida.
Observou-se empiricamente que tamanhos de lote menores não só têm uma dinâmica de treinamento mais rápida, mas também generalização para o conjunto de dados de teste versus tamanhos de lote maiores. Mas esta afirmação tem seus limites. Sabemos que um tamanho de lote de 1 geralmente funciona muito mal. É geralmente aceito que existe um “ponto ideal” para o tamanho do lote entre 1 e todo o conjunto de dados de treinamento que fornecerá a melhor generalização. Esse “ponto ideal” geralmente depende do conjunto de dados e do modelo em questão.
A razão para uma melhor generalização é vagamente atribuída à existência de “ruído” no treinamento de pequeno tamanho de lote. Como os sistemas de redes neurais são extremamente propensos a ajustes excessivos (overfitting), a ideia é que a visualização de vários tamanhos de lote pequenos, cada lote sendo uma representação “ruidosa” de todo o conjunto de dados, causará uma espécie de dinâmica de “tug-and-pull”. Essa dinâmica evita que a rede neural se ajuste excessivamente no conjunto de treinamento e, portanto, tenha um desempenho ruim no conjunto de testes.
Definição do Problema
O problema exato que será investigado é o da classificação. Dada uma imagem X, o objetivo é prever o rótulo da imagem y. No caso do conjunto de dados MNIST, X são imagens em preto-e-branco dos dígitos 0 a 9 e y são as etiquetas de dígitos correspondentes “0” a “9”. Nosso modelo de escolha é uma rede neural. Especificamente, usaremos um Perceptron Multicamada (MLP). Salvo disposição em contrário, este é o modelo padrão foi usado no experimento:
- 2 camadas ocultas totalmente conectadas (FC), 1024 unidades cada
- Função de ativação ReLU
- Função de perda: logaritmo negativo
- Otimizador: SGD (Stochastic Gradient Descent)
- Taxa de aprendizagem: 0,01
- Épocas: 30
Em última análise, a pergunta que queremos responder é “qual tamanho de lote devo usar ao treinar uma rede neural?”
Efeito do Tamanho do Lote
A primeira coisa que devemos fazer para confirmar o problema que estamos tentando investigar é mostrar a dependência entre o intervalo de generalização e o tamanho do lote. Eu tenho me referido à métrica que estamos considerando como “gap de generalização”. Essa é tipicamente a medida de autores sobre o tema usada em artigos e papers, mas para simplicidade em nosso estudo nós apenas nos preocuparemos com a precisão do teste sendo a mais alta possível. Como veremos, a precisão de treinamento e teste dependerá do tamanho do lote, por isso é mais significativo falar sobre a precisão de teste em vez do gap de generalização. Mais especificamente, queremos que a precisão do teste depois de um grande número de épocas de treinamento, seja alta. Quantas épocas é um “grande número de épocas”? Idealmente, isso é definido como o número de épocas de treinamento necessárias, de modo que qualquer treinamento adicional forneça pouco ou nenhum aumento na precisão de teste. Na prática, isso é difícil de determinar e teremos que adivinhar quantas épocas são apropriadas para alcançar um comportamento ideal. Apresento as precisões de teste do nosso modelo de rede neural treinado usando diferentes tamanhos de lote abaixo (para aprender a fazer tudo isso na prática, clique aqui).
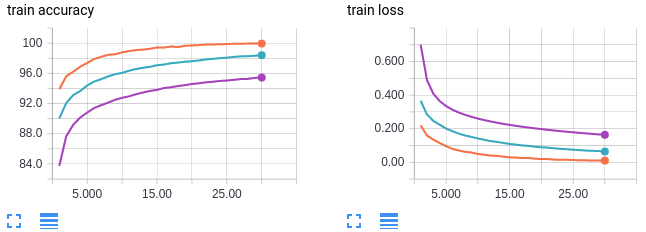
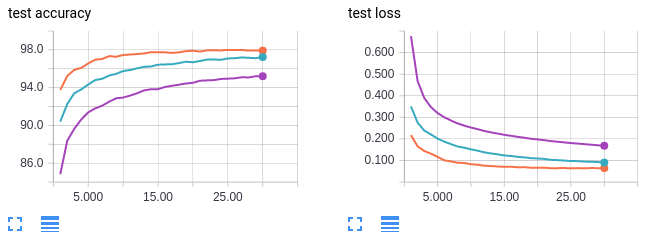
Curvas em laranja: tamanho do lote 64
Curvas em verde: tamanho do lote 256
Curvas em lilás: tamanho do lote 1024
Descoberta: tamanhos maiores de lotes levam a uma precisão menor nos dados de teste.
O eixo x mostra o número de épocas de treinamento. O eixo y é rotulado para cada plotagem. MNIST é obviamente um conjunto de dados fácil de treinar; podemos alcançar 100% de precisão em treino e 98% em teste com apenas nosso modelo MLP base no tamanho de lote 64. Além disso, vemos uma clara tendência entre o tamanho do lote e a precisão do teste (e treinamento!). A nossa primeira conclusão é a seguinte: maiores tamanhos de lotes levam a uma menor precisão nos dados de teste. Esses padrões parecem existir em seu extremo para o conjunto de dados MNIST. Eu tentei tamanho de lote igual a 2 e alcançou uma precisão de teste ainda melhor de 99% (versus 98% para tamanho de lote 64)! Como aviso prévio, não espere que tamanhos de lote muito baixos, como 2, funcionem bem em conjuntos de dados mais complexos.
Mas neste experimento não consideramos alterações na taxa de aprendizagem. Poderíamos aumentar a acurácia em teste com tamanhos de lote maiores, ajustando a taxa de aprendizagem (learning rate)? Não perca o próximo capítulo para descobrir! Até lá.
Referências:
Don’t Decay the Learning Rate, Increase the Batch Size
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Effect of batch size on training dynamics
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning (material usado com autorização do autor)
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

