Capítulo 50 – A Matemática da Dissipação do Gradiente e Aplicações das RNNs

No Capítulo 34 nós discutimos sobre o problema da dissipação do gradiente e a dificuldade em treinar as redes neurais artificiais. Com as RNNs esse problema é ainda mais acentuado e por isso vamos agora estudar A Matemática da Dissipação do Gradiente e Aplicações das RNNs e compreender matematicamente porque o problema acontece.

Mencionamos anteriormente que as RNNs têm dificuldades em aprender dependências de longo alcance – interações entre palavras que estão separadas por vários passos, por exemplo. Isso é problemático porque o significado de uma frase em português é geralmente determinado por palavras que não são muito próximas: “O homem que usava uma peruca entrou no bar”. A frase é realmente sobre um homem entrando em um bar, não sobre a peruca. Mas é improvável que uma RNN simples seja capaz de capturar essas informações. Para entender porque, vamos dar uma olhada mais de perto no gradiente que calculamos no capítulo anterior:

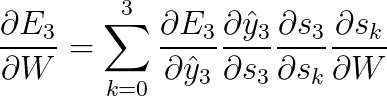
Observe que:

é uma regra de cadeia em si! Por exemplo:

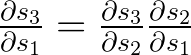
Observe também que, como estamos tomando a derivada de uma função vetorial em relação a um vetor, o resultado é uma matriz (chamada de matriz jacobiana) cujos elementos são todos derivadas pointwise. Podemos reescrever o gradiente acima da seguinte forma:

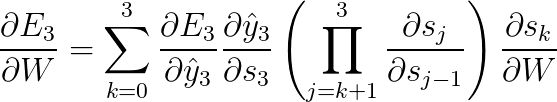
Acontece (esse paper explica isso em detalhes) que a norma (na álgebra linear, análise funcional e áreas relacionadas da matemática, uma norma é uma função que atribui um comprimento ou tamanho estritamente positivo a cada vetor em um espaço vetorial – exceto para o vetor zero, ao qual é atribuído um comprimento de zero), que você pode pensar como um valor absoluto, da matriz jacobiana acima tem um limite superior de 1. Isso porque a nossa função de ativação tanh (ou sigmóide) mapeia todos os valores em um intervalo entre -1 e 1, e a derivada é limitada por 1 (1/4 no caso de sigmoide) também:

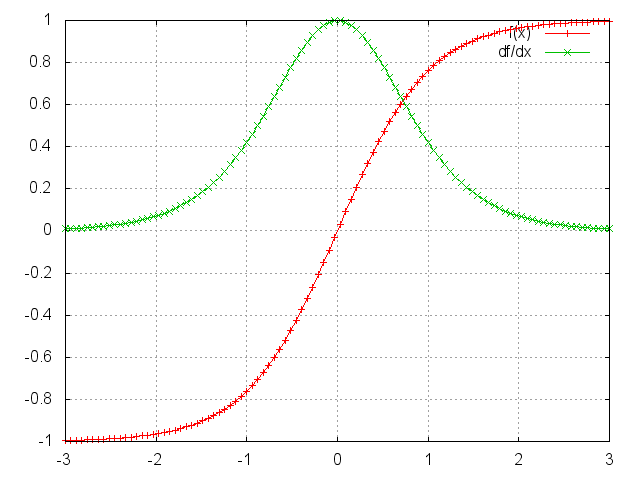
Você pode ver que as funções tanh e sigmoid têm derivadas de 0 em ambas as extremidades, onde se aproximam de uma linha plana. Quando isso acontece, dizemos que os neurônios correspondentes estão saturados. Eles têm um gradiente nulo e conduzem outros gradientes nas camadas anteriores para 0. Assim, com valores pequenos nas multiplicações de matriz e múltiplas matrizes (t-k em particular) os valores de gradiente estão diminuindo exponencialmente rápido, desaparecendo completamente após alguns passos de tempo.

Contribuições gradientes de etapas “longínquas” se tornam zero e o estado nessas etapas não contribui para o que a rede está aprendendo: a rede acaba não aprendendo dependências de longo alcance. Dissipações do gradiente não são exclusivos das RNNs e também acontecem em Redes Neurais Profundas Feedforward. Mas as RNNs tendem a ser muito profundas (tão profundas quanto a duração da sentença, em um problema de Processamento de Linguagem Natural por exemplo), o que torna o problema muito mais comum.

É fácil imaginar que, dependendo de nossas funções de ativação e parâmetros de rede, poderíamos obter explosão em vez de dissipação de gradientes, se os valores da matriz Jacobiana forem grandes. Na verdade, isso é chamado de problema de explosão do gradiente. A razão pela qual as dissipações do gradiente receberam mais atenção do que as explosões é dupla. Por um lado, explosão de gradientes são óbvias. Seus gradientes se tornarão NaN (não um número) e seu programa falhará.

Em segundo lugar, recortar os gradientes em um limiar pré-definido é uma solução muito simples e eficaz para evitar a explosão dos gradientes. As dissipações dos gradientes são mais problemáticas porque não são óbvias quando ocorrem ou é mais complicado lidar com elas.

Felizmente, existem algumas maneiras de combater o problema da dissipação do gradiente. A inicialização adequada da matriz W pode reduzir o efeito do problema. Ou seja, aplicamos regularização. Uma solução mais interessante é usar as funções de ativação ReLU em vez de tanh ou sigmóide. A derivada ReLU é uma constante de 0 ou 1, por isso não é tão provável que sofra de dissipação do gradiente.

Uma solução ainda mais popular é usar as arquiteturas Long Short-Term Memory (LSTM) ou Gated Recurrent Unit (GRU). As LSTMs foram propostas pela primeira vez em 1997 e são os modelos talvez mais amplamente usados em Processamento de Linguagem Natural atualmente. As GRUs, propostas pela primeira vez em 2014, são versões simplificadas das LSTMs. Ambas as arquiteturas RNN foram explicitamente projetadas para lidar com dissipação do gradiente e aprender eficientemente dependências de longo alcance. Vamos cobrir as duas arquiteturas nos próximos capítulos.

Mas o que podemos fazer com as RNNs?

As RNNs mostraram grande sucesso em muitas tarefas de Processamento de Linguagem Natural. Neste ponto, devo mencionar que os tipos de RNN mais usados são as LSTMs, que são muito melhores na captura de dependências de longo prazo do que as RNNs em sua arquitetura padrão. Mas não se preocupe, as LSTMs são essencialmente a mesma coisa que as RNNs, mas apenas têm uma maneira diferente de computar o estado oculto. Cobriremos as LSTMs com mais detalhes no próximo capítulo. Aqui estão alguns exemplos de aplicações de RNNs em Processamento de Linguagem Natural (o que não é uma lista definitiva).

Modelagem de Linguagem e Geração de Texto

Dada uma sequência de palavras, queremos prever a probabilidade de cada palavra dada às palavras anteriores. Os Modelos de Linguagem nos permitem medir a probabilidade de uma sentença, que é uma entrada importante para a Tradução Automática (já que as sentenças de alta probabilidade estão normalmente corretas). Um efeito colateral de poder prever a próxima palavra é que obtemos um modelo generativo, que nos permite gerar um novo texto por amostragem a partir das probabilidades de saída. E dependendo de quais são nossos dados de treinamento, podemos gerar todos os tipos de coisas.

Em Modelagem de Linguagem, nossa entrada é tipicamente uma sequência de palavras (codificadas como vetores únicos), e nossa saída é a sequência de palavras previstas. Ao treinar a rede, definimos ot = x{t + 1}, pois queremos que a saída na etapa t seja a próxima palavra real.

Machine Translation

A tradução automática é semelhante à modelagem de linguagem, pois nossa entrada é uma sequência de palavras em nosso idioma de origem (por exemplo português). Queremos produzir uma sequência de palavras em nosso idioma de destino (por exemplo, inglês). A principal diferença é que nossa saída só é iniciada depois de termos visto a entrada completa, porque a primeira palavra de nossas sentenças traduzidas pode exigir informações capturadas da sequência de entrada completa.

Reconhecimento de Fala

Dada uma sequência de entrada de sinais acústicos de uma onda sonora, podemos prever uma sequência de segmentos fonéticos juntamente com suas probabilidades.

Gerar Descrições de Imagens

Juntamente com as redes neurais convolucionais, as RNNs foram usados como parte de um modelo para gerar descrições de imagens não rotuladas. É incrível como isso parece funcionar. O modelo combinado alinha as palavras geradas com os recursos encontrados nas imagens.

Continuamos no próximo capítulo.

Referências:

Matemática Para Data Science

A Recursive Recurrent Neural Network for Statistical Machine Translation

Sequence to Sequence Learning with Neural Networks

Recurrent Neural Networks Cheatsheet

On the difficulty of training recurrent neural networks

A Beginner’s Guide to LSTMs and Recurrent Neural Networks

Recurrent Neural Networks Tutorial, Part 1 – Introduction to RNNs

Recurrent Neural Networks Tutorial, Part 3 – Backpropagation Through Time and Vanishing Gradients

Train longer, generalize better: closing the generalization gap in large batch training of neural networks

Practical Recommendations for Gradient-Based Training of Deep Architectures