Capítulo 21 – Afinal, Por Que a Regularização Ajuda a Reduzir o Overfitting?
Vimos no capítulo anterior que a regularização ajuda a reduzir o overfitting. Isso é encorajador, mas, infelizmente, não é óbvio porque a regularização ajuda a resolver o overfitting! Uma história padrão que as pessoas contam para explicar o que está acontecendo segue mais ou menos esse raciocínio: pesos menores são, em certo sentido, de menor complexidade e, portanto, fornecem uma explicação mais simples e mais poderosa para os dados e devem, normalmente, ser preferidos. É uma história bastante concisa e contém vários elementos que talvez pareçam dúbios ou mistificadores. Vamos descompactar essa explicação e examiná-la criticamente. Afinal, Por Que a Regularização Ajuda a Reduzir o Overfitting?
Para fazer isso, vamos supor que temos um conjunto de dados simples para o qual desejamos construir um modelo:
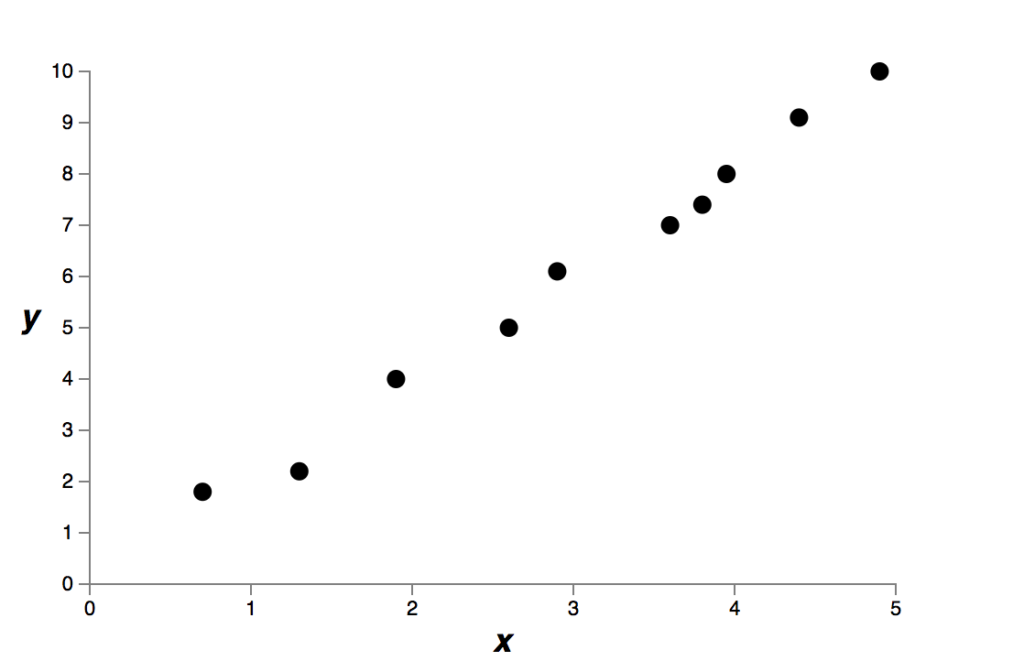
Implicitamente, estamos estudando algum fenômeno do mundo real aqui, com x e y representando dados desse fenômeno. Nosso objetivo é construir um modelo que nos permita prever y como uma função de x (isso é o que fazemos em Machine Learning). Poderíamos tentar usar redes neurais para construir esse modelo, mas vou fazer algo ainda mais simples: vou tentar modelar y como um polinômio em x. Estou fazendo isso em vez de usar redes neurais porque usar polinômios tornará as coisas particularmente transparentes. Uma vez que tenhamos entendido o caso polinomial, vamos traduzir para redes neurais.
Há dez pontos no gráfico acima, o que significa que podemos encontrar um único polinômio de 9ª ordem y = a0x9 + a1x8 +… + a9 que se ajusta exatamente aos dados. Aqui está o gráfico desse polinômio:
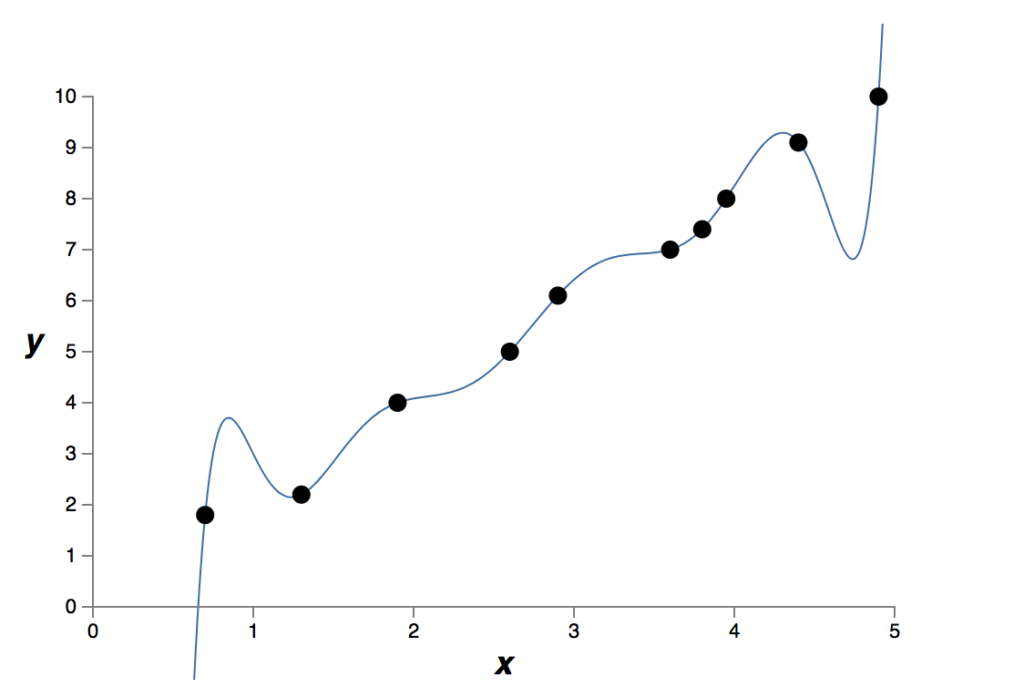
Isso fornece um ajuste exato. Mas também podemos obter um bom ajuste usando o modelo linear y = 2x:
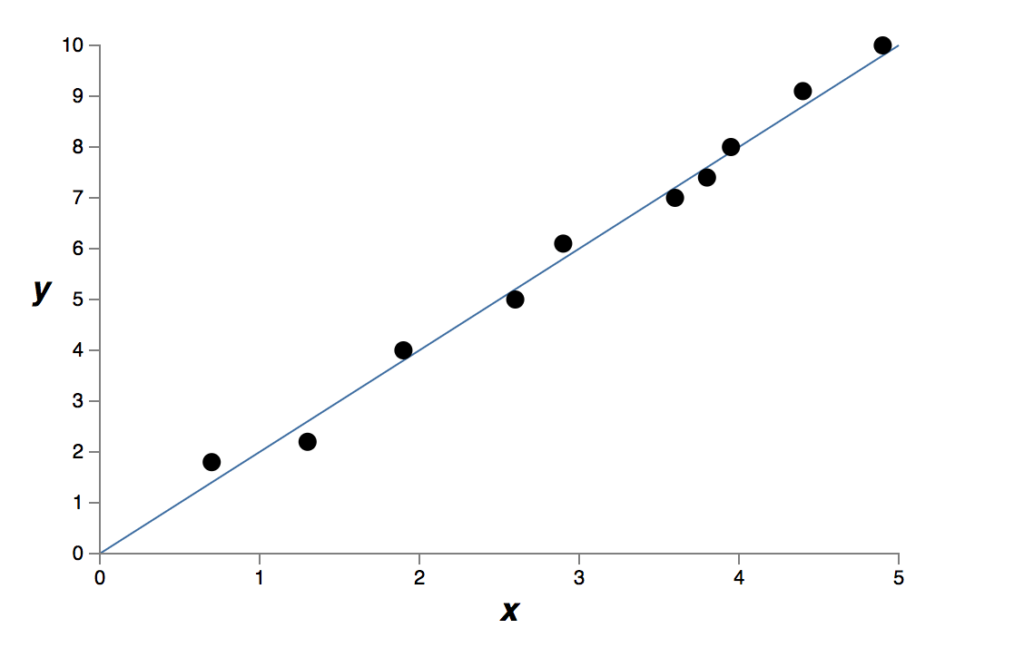
Qual destes é o melhor modelo? E qual modelo é mais provável de generalizar bem a outros exemplos do mesmo fenômeno do mundo real?
Essas são questões difíceis. De fato, não podemos determinar com certeza a resposta para qualquer uma das perguntas acima, sem muito mais informações sobre o fenômeno do mundo real que estamos analisando (é onde entra a experiência do Cientista de Dados sobre áreas de negócio). Mas vamos considerar duas possibilidades: (1) o polinômio de 9ª ordem é, de fato, o modelo que realmente descreve o fenômeno do mundo real, e o modelo, portanto, generalizará perfeitamente; (2) o modelo correto é y = 2x, mas há um pequeno ruído adicional devido a, digamos, erros de medição, e é por isso que o modelo não é um ajuste exato.
Não é possível a priori dizer qual dessas duas possibilidades está correta (ou, na verdade, se alguma terceira possibilidade é válida). Logicamente, qualquer uma poderia ser verdade. E não é uma diferença trivial. É verdade que nos dados fornecidos há apenas uma pequena diferença entre os dois modelos. Mas suponha que queremos predizer o valor de y correspondendo a um grande valor de x, muito maior do que qualquer um mostrado nos gráficos acima. Se tentarmos fazer isso, haverá uma diferença dramática entre as previsões dos dois modelos, já que o modelo polinomial de 9ª ordem passa a ser dominado pelo termo x9, enquanto o modelo linear permanece, bem, linear.
Um ponto de vista é dizer que, na ciência, devemos seguir a explicação mais simples, a menos que sejamos obrigados a fazer o contrário. Quando encontramos um modelo simples que parece explicar muitos dados, somos tentados a gritar “Eureka!” Afinal, parece improvável que uma explicação simples ocorra apenas por coincidência. Em vez disso, suspeitamos que o modelo deve estar expressando alguma verdade subjacente sobre o fenômeno. No caso em questão, o modelo y = 2x + ruído parece muito mais simples que y = a0x9 + a1x8 +…. Seria surpreendente se essa simplicidade tivesse ocorrido por acaso, e então suspeitamos que y = 2x + ruído expressa alguma verdade subjacente. Nesse ponto de vista, o modelo de 9ª ordem está realmente aprendendo apenas os efeitos do ruído local. E assim, enquanto o modelo de 9ª ordem funciona perfeitamente para esses pontos de dados particulares, o modelo não conseguirá generalizar para outros pontos de dados, e o modelo linear terá maior poder preditivo.
Vamos ver o que esse ponto de vista significa para redes neurais. Suponha que nossa rede tenha, na maioria das vezes, pequenos pesos, como tenderá a acontecer em uma rede regularizada. O tamanho menor dos pesos significa que o comportamento da rede não mudará muito se alterarmos algumas entradas aleatórias aqui e ali. Isso dificulta que uma rede regularizada aprenda os efeitos do ruído local nos dados. Pense nisso como uma maneira de fazer com que as evidências não importem muito para a saída da rede. Em vez disso, uma rede regularizada aprende a responder a tipos de evidências que são vistas com frequência em todo o conjunto de treinamento. Por outro lado, uma rede com grandes pesos pode alterar bastante seu comportamento em resposta a pequenas alterações na entrada. Assim, uma rede não regularizada pode usar grandes pesos para aprender um modelo complexo que contém muitas informações sobre o ruído nos dados de treinamento. Em suma, as redes regularizadas são levadas a construir modelos relativamente simples baseados em padrões vistos frequentemente nos dados de treinamento e são resistentes às peculiaridades de aprendizagem do ruído nos dados de treinamento. A esperança é que isso forçará nossas redes a aprender de verdade sobre o fenômeno em questão e a generalizar melhor o que aprendem.
Com isso dito, e mantendo a necessidade de cautela em mente, é um fato empírico que as redes neurais regularizadas geralmente generalizam melhor do que as redes não regularizadas. A verdade é que ninguém ainda desenvolveu uma explicação teórica inteiramente convincente para explicar porque a regularização ajuda a generalizar as redes. De fato, os pesquisadores continuam a escrever artigos nos quais tentam abordagens diferentes à regularização, comparam-nas para ver qual funciona melhor e tentam entender por que diferentes abordagens funcionam melhor ou pior. Embora muitas vezes ajude, não temos uma compreensão sistemática inteiramente satisfatória do que está acontecendo, apenas heurísticas incompletas e regras gerais.
Há um conjunto mais profundo de questões aqui, questões que vão para o coração da ciência. É a questão de como generalizamos. A regularização pode nos dar uma varinha mágica computacional que ajuda nossas redes a generalizar melhor, mas não nos dá uma compreensão baseada em princípios de como a generalização funciona, nem de qual é a melhor abordagem.
Isso é particularmente irritante porque na vida cotidiana, nós humanos generalizamos bem. Mostradas apenas algumas imagens de um elefante, uma criança aprenderá rapidamente a reconhecer outros elefantes. É claro que eles podem ocasionalmente cometer erros, talvez confundindo um rinoceronte com um elefante, mas em geral esse processo funciona notavelmente com precisão. Então nós temos um sistema – o cérebro humano – com um grande número de parâmetros livres. E depois de ser mostrado apenas uma ou algumas imagens de treinamento, o sistema aprende a generalizar para outras imagens. Nossos cérebros estão, em certo sentido, se regularizando incrivelmente bem! Como fazemos isso? Neste ponto não sabemos. Espero que nos próximos anos desenvolvamos técnicas mais poderosas de regularização em redes neurais artificiais, técnicas que permitirão que as redes neurais generalizem bem, mesmo a partir de pequenos conjuntos de dados.
De fato, nossas redes já generalizam melhor do que se poderia esperar a priori. Uma rede com 100 neurônios ocultos tem quase 80.000 parâmetros. Temos apenas 50.000 imagens em nossos dados de treinamento. É como tentar encaixar um polinômio de grau 80.000 em 50.000 pontos de dados. Consequentemente, nossa rede deve se ajustar muito bem. E, no entanto, como vimos anteriormente, essa rede realmente faz um ótimo trabalho generalizando. Por que esse é o caso? Não é bem entendido. Foi conjecturado que “a dinâmica do aprendizado de gradiente descendente em redes multicamadas tem um efeito de ‘autorregulação'”. Isso é excepcionalmente bom, mas também é um tanto inquietante que não entendemos porque exatamente isso ocorre e por isso muitas vezes modelos de redes neurais profundas são chamados de “caixa preta”. Enquanto isso, adotaremos a abordagem pragmática e usaremos a regularização sempre que pudermos. Nossas redes neurais serão melhores assim.
Deixe-me concluir esta seção voltando a um detalhe que deixei inexplicado antes: o fato de que a regularização L2 não restringe os vieses. É claro que seria fácil modificar o procedimento de regularização para regularizar os vieses. Empiricamente, fazendo isso muitas vezes não muda muito os resultados, então, em certa medida, é apenas uma convenção se regularizar os vieses ou não. No entanto, vale a pena notar que ter um grande viés não torna um neurônio sensível às suas entradas da mesma maneira que ter pesos grandes. Portanto, não precisamos nos preocupar com grandes vieses que permitem que nossa rede aprenda o ruído em nossos dados de treinamento. Ao mesmo tempo, permitir grandes vieses dá às nossas redes mais flexibilidade no comportamento – em particular, grandes vieses facilitam a saturação dos neurônios, o que às vezes é desejável. Por essas razões, geralmente não incluímos termos de viés quando regularizamos a rede neural.
Você já percebeu que regularização é um assunto importante quando tratamos de redes neurais. Nos próximos capítulos estudaremos mais duas técnicas de regularização: Regularização L1 e Dropout! Não perca!
Referências:
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning
Pattern Recognition and Machine Learning

