Capítulo 14 – Algoritmo Backpropagation Parte 1 – Grafos Computacionais e Chain Rule
No último capítulo, vimos como as redes neurais podem aprender seus pesos e bias usando o algoritmo de gradiente descendente. Houve, no entanto, uma lacuna na nossa explicação: não discutimos como calcular o gradiente da função de custo. Neste capítulo, explicaremos sobre um algoritmo usado para calcular esses gradientes, um algoritmo conhecido como backpropagation. Como esse tema é a essência do treinamento de redes neurais, vamos dividí-lo em dois capítulos. Vamos começar com Algoritmo Backpropagation Parte 1 – Grafos Computacionais e Chain Rule.
O backpropagation é indiscutivelmente o algoritmo mais importante na história das redes neurais – sem backpropagation, seria quase impossível treinar redes de aprendizagem profunda da forma que vemos hoje. O backpropagation pode ser considerado a pedra angular das redes neurais modernas e consequentemente do Deep Learning.
O algoritmo backpropagation foi originalmente introduzido na década de 1970, mas sua importância não foi totalmente apreciada até um famoso artigo de 1986 de David Rumelhart, Geoffrey Hinton e Ronald Williams. Esse artigo descreve várias redes neurais em que o backpropagation funciona muito mais rapidamente do que as abordagens anteriores de aprendizado, possibilitando o uso de redes neurais para resolver problemas que antes eram insolúveis.
O backpropagation é o algoritmo-chave que faz o treinamento de modelos profundos algo computacionalmente tratável. Para as redes neurais modernas, ele pode tornar o treinamento com gradiente descendente até dez milhões de vezes mais rápido, em relação a uma implementação ingênua. Essa é a diferença entre um modelo que leva algumas horas ou dias para treinar e e outro que poderia levar anos (sem exagero).
Além de seu uso em Deep Learning, o backpropagation é uma poderosa ferramenta computacional em muitas outras áreas, desde previsão do tempo até a análise da estabilidade numérica. De fato, o algoritmo foi reinventado pelo menos dezenas de vezes em diferentes campos. O nome geral, independente da aplicação, é “diferenciação no modo reverso”.
Fundamentalmente, backpropagation é uma técnica para calcular derivadas rapidamente (não sabe o que é derivada? Consulte o link para um excelente vídeo em português explicando esse conceito em detalhes nas referências ao final deste capítulo). E é um truque essencial, não apenas em Deep Learning, mas em uma ampla variedade de situações de computação numérica. E para compreender backpropagation de forma efetiva, vamos primeiro compreender o conceito de grafo computacional e chain rule.
Grafo Computacional
Grafos computacionais são uma boa maneira de pensar em expressões matemáticas. O conceito de grafo foi introduzido por Leonhard Euler em 1736 para tentar resolver o problema das Pontes de Konigsberg. Grafos são modelos matemáticos para resolver problemas práticos do dia a dia, com várias aplicações no mundo real tais como: circuitos elétricos, redes de distribuição, relações de parentesco entre pessoas, análise de redes sociais, logística, redes de estradas, redes de computadores e muito mais. Grafos são muito usados para modelar problemas em computação.
Um Grafo é um modelo matemático que representa relações entre objetos. Um grafo G = (V, E) consiste de um conjunto de vértices V (também chamados de nós), ligados por um conjunto de bordas ou arestas E. Para aprender sobre grafos em mais detalhes, clique aqui.
Por exemplo, considere a expressão:
e = (a + b) ∗ (b + 1)
Existem três operações: duas adições e uma multiplicação. Para facilitar a compreensão sobre isso, vamos introduzir duas variáveis intermediárias c e d para que a saída de cada função tenha uma variável. Nós agora temos:
c = a+b
d = b+1
e = c∗d
Para criar um grafo computacional, fazemos cada uma dessas operações nos nós, juntamente com as variáveis de entrada. Quando o valor de um nó é a entrada para outro nó, uma seta vai de um para outro e temos nesse caso um grafo direcionado.
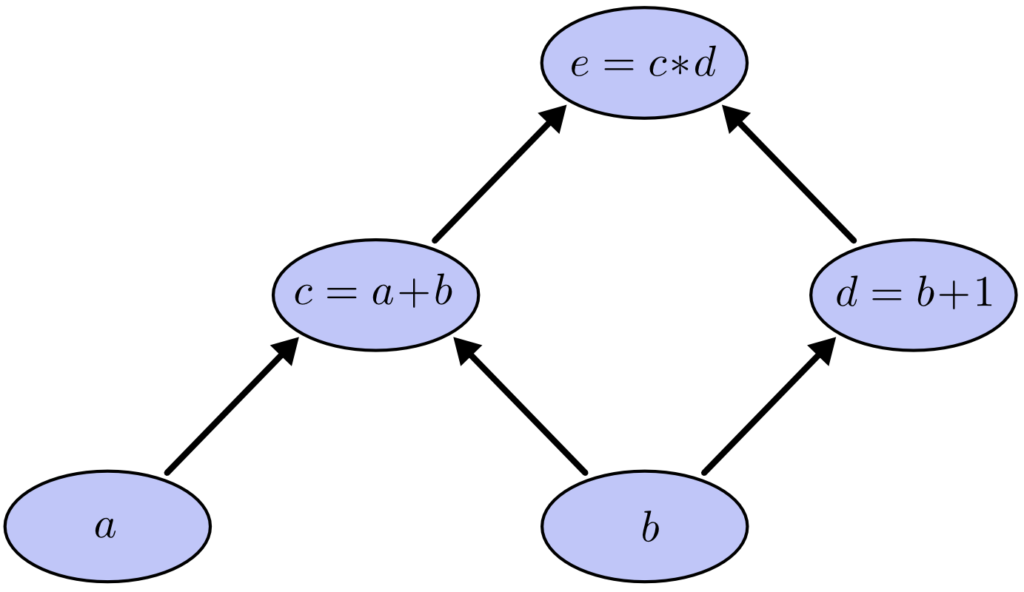
Esses tipos de grafos surgem o tempo todo em Ciência da Computação, especialmente ao falar sobre programas funcionais. Eles estão intimamente relacionados com as noções de grafos de dependência e grafos de chamadas. Eles também são a principal abstração por trás do popular framework de Deep Learning, o TensorFlow.
Podemos avaliar a expressão definindo as variáveis de entrada para determinados valores e computando os nós através do grafo. Por exemplo, vamos definir a = 2 e b = 1:
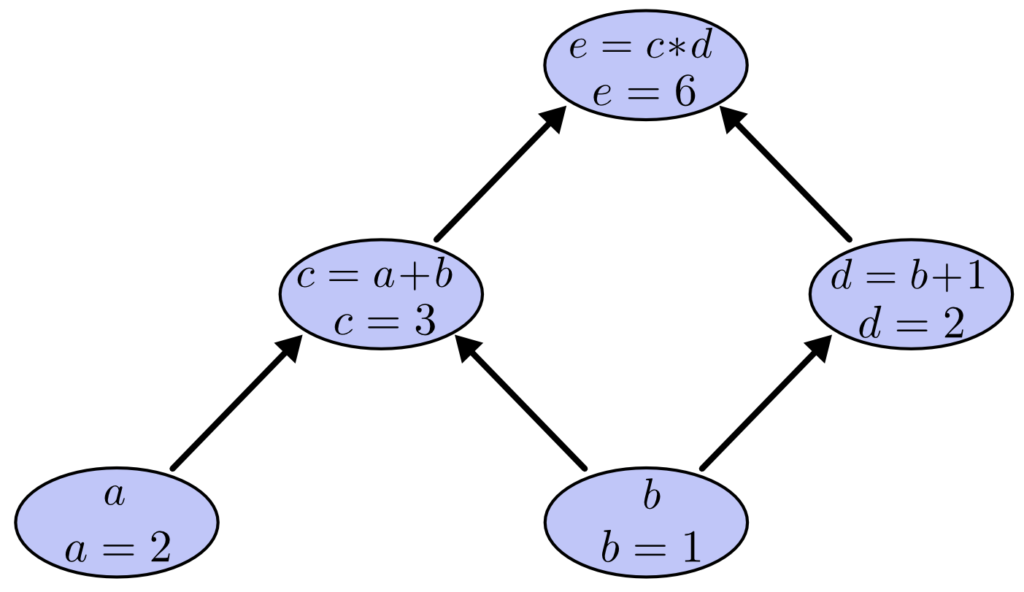
A expressão, nesse exemplo, é avaliada como 6.
Derivadas em Grafos Computacionais
Se alguém quiser entender derivadas em um grafo computacional, a chave é entender as derivadas nas bordas (arestas que conectam os nós no grafo). Se a afeta diretamente c, então queremos saber como isso afeta c. Se a muda um pouco, como c muda? Chamamos isso de derivada parcial de c em relação a a.
Para avaliar as derivadas parciais neste grafo, precisamos da regra da soma e da regra do produto:
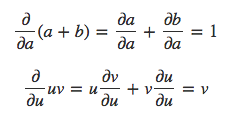
Abaixo, o grafo tem a derivada em cada borda (aresta) rotulada.
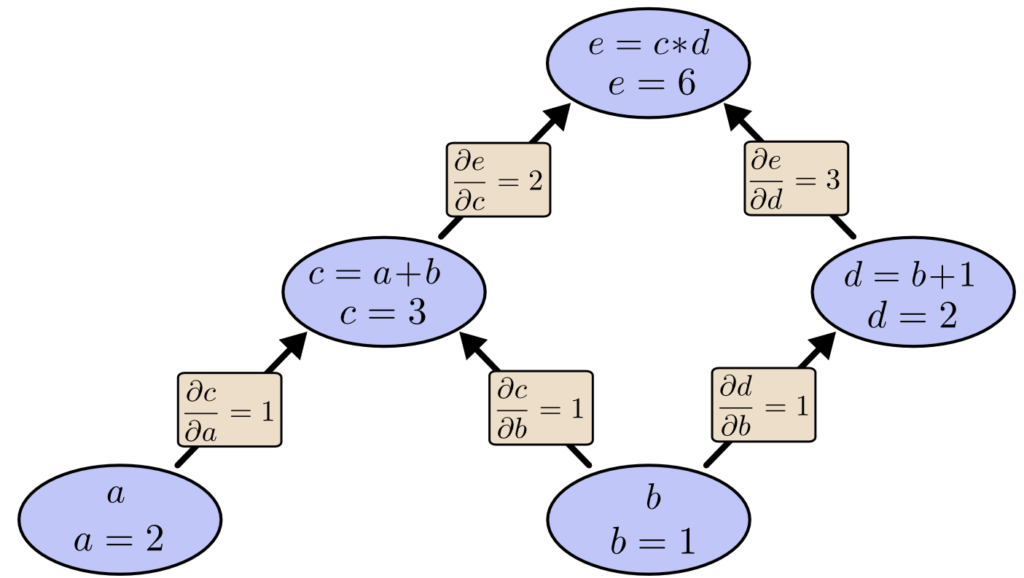
E se quisermos entender como os nós que não estão diretamente conectados afetam uns aos outros? Vamos considerar como e é afetado por a. Se mudarmos a uma velocidade de 1, c também muda a uma velocidade de 1. Por sua vez, c mudando a uma velocidade de 1 faz com que e mude a uma velocidade de 2. Então e muda a uma taxa de 1 ∗ 2 em relação a a (analise o diagrama acima para visualizar isso).
A regra geral é somar todos os caminhos possíveis de um nó para o outro, multiplicando as derivadas em cada aresta do caminho. Por exemplo, para obter a derivada de e em relação a b, obtemos:
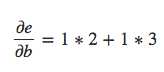
Isso explica como b afeta e através de c e também como isso afeta d.
Essa regra geral de “soma sobre caminhos” é apenas uma maneira diferente de pensar sobre a regra da cadeia multivariada ou chain rule.
Fatorando os Caminhos
O problema com apenas “somar os caminhos” é que é muito fácil obter uma explosão combinatória no número de caminhos possíveis.
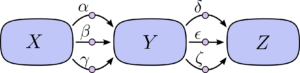
No diagrama acima, existem três caminhos de X a Y, e mais três caminhos de Y a Z. Se quisermos obter a derivada ∂Z/∂X somando todos os caminhos, precisamos calcular 3 ∗ 3 = 9 caminhos:
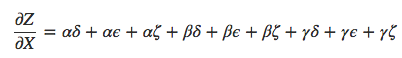
O exemplo acima só tem nove caminhos, mas seria fácil o número de caminhos crescer exponencialmente à medida que o grafo se torna mais complicado. Em vez de apenas ingenuamente somar os caminhos, seria muito melhor fatorá-los:
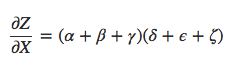
É aí que entram a “diferenciação de modo de avanço” (forward-mode differentiation ou forward pass) e a “diferenciação de modo reverso” (reverse-mode differentiation ou backpropagation). Eles são algoritmos para calcular a soma de forma eficiente fatorando os caminhos. Em vez de somar todos os caminhos explicitamente, eles calculam a mesma soma de forma mais eficiente, mesclando os caminhos juntos novamente em cada nó. De fato, os dois algoritmos tocam cada borda exatamente uma vez!
A diferenciação do modo de avanço inicia em uma entrada para o grafo e se move em direção ao final. Em cada nó, soma todos os caminhos que se alimentam. Cada um desses caminhos representa uma maneira na qual a entrada afeta esse nó. Ao adicioná-los, obtemos a maneira total em que o nó é afetado pela entrada, isso é a derivada.
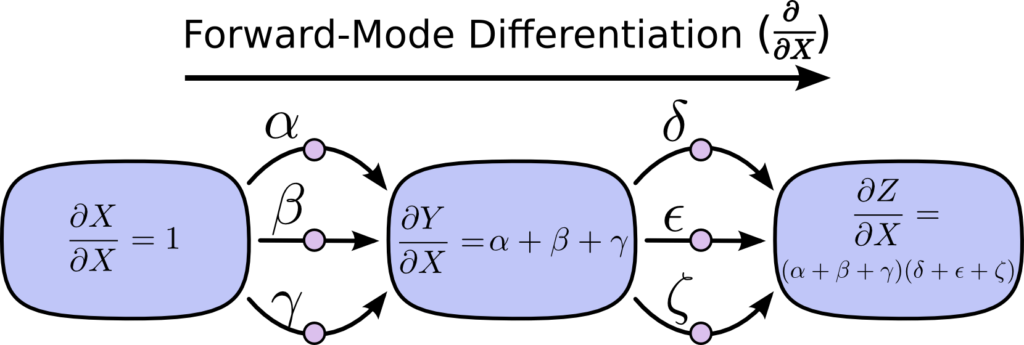
Embora você provavelmente não tenha pensado nisso em termos de grafos, a diferenciação no modo de avanço é muito parecida com o que você aprendeu implicitamente caso tenha feito alguma introdução a Cálculo.
A diferenciação no modo reverso, por outro lado, começa na saída do grafo e se move em direção ao início (ou seja, se retropropaga ou backpropagation). Em cada nó, ele mescla todos os caminhos originados nesse nó.

A diferenciação do modo de avanço rastreia como uma entrada afeta todos os nós. A diferenciação no modo reverso rastreia como cada nó afeta uma saída. Ou seja, a diferenciação de modo de avanço aplica o operador ∂/∂X a cada nó, enquanto a diferenciação de modo reverso aplica o operador ∂Z/∂ a cada nó. Se isso parece o conceito de programação dinâmica, é porque é exatamente isso! (acesse um material sobre programação dinâmica nas referências ao final do capítulo)
Nesse ponto, você pode se perguntar porque alguém se importaria com a diferenciação no modo reverso. Parece uma maneira estranha de fazer a mesma coisa que o modo de avanço. Existe alguma vantagem? Vamos considerar nosso exemplo original novamente:

Podemos usar a diferenciação de modo de avanço de b para cima. Isso nos dá a derivada de cada nó em relação a b.
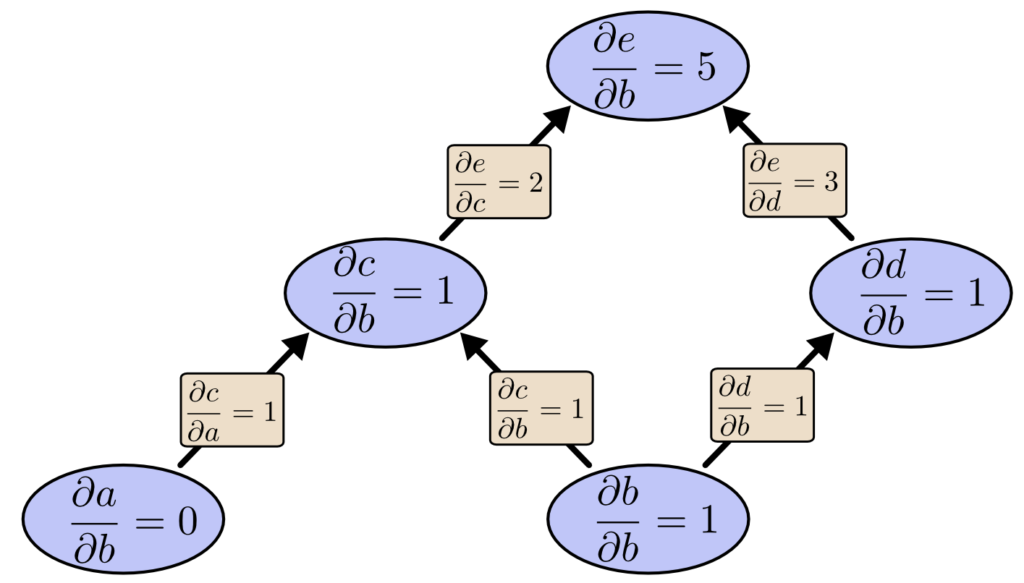
Nós calculamos ∂e/∂b, a derivada de nossa saída em relação a um de nossos inputs. E se fizermos a diferenciação de modo reverso de e para baixo? Isso nos dá a derivada de e em relação a todos os nós:
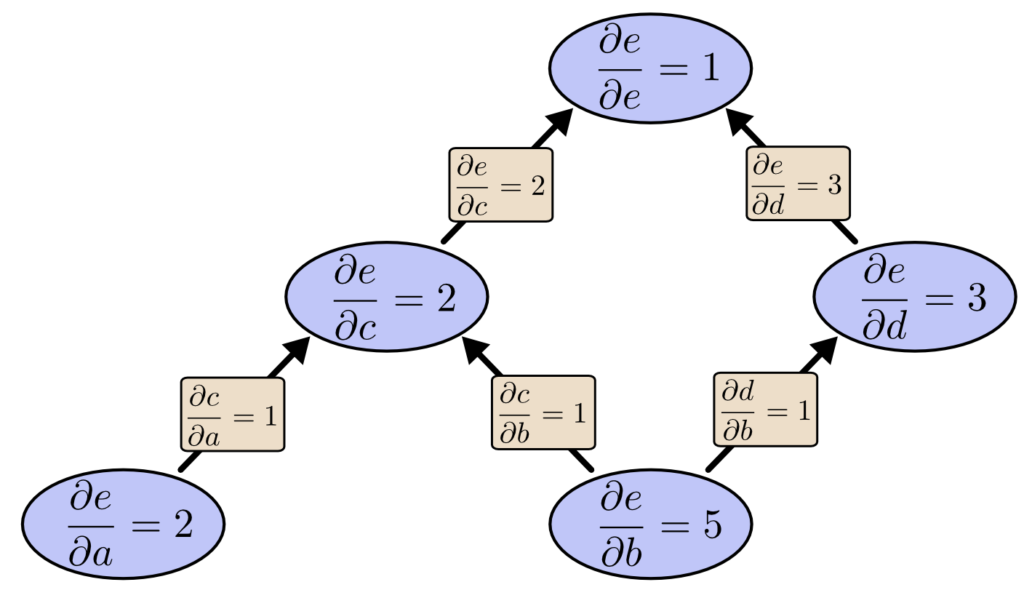
Quando digo que a diferenciação no modo reverso nos dá a derivada de e em relação a cada nó, eu realmente quero dizer cada nó. Temos tanto ∂e/∂a quanto ∂e/∂b, as derivadas de e em relação a ambas as entradas. A diferenciação no modo de avanço nos deu a derivada de nossa saída em relação a uma única entrada, mas a diferenciação no modo reverso nos dá todos eles.
Para este grafo, isso é apenas um fator de duas velocidades, mas imagine uma função com um milhão de entradas e uma saída. A diferenciação no modo de avanço exigiria que passássemos pelo grafo um milhão de vezes para obter as derivadas. Diferenciação no modo reverso pode fazer isso em uma só passada! Uma aceleração de um fator de um milhão é bem legal e explica porque conseguimos treinar um modelo de rede neural profunda em tempo razoável.
Ao treinar redes neurais, pensamos no custo (um valor que descreve o quanto uma rede neural é ruim) em função dos parâmetros (números que descrevem como a rede se comporta). Queremos calcular as derivadas do custo em relação a todos os parâmetros, para uso em descida do gradiente. Entretanto, muitas vezes, há milhões ou até dezenas de milhões de parâmetros em uma rede neural. Então, a diferenciação no modo reverso, chamada de backpropagation no contexto das redes neurais, nos dá uma velocidade enorme!
Existem casos em que a diferenciação de modo de avanço faz mais sentido? Sim, existem! Onde o modo reverso fornece as derivadas de uma saída em relação a todas as entradas, o modo de avanço nos dá as derivadas de todas as saídas em relação a uma entrada. Se tiver uma função com muitas saídas, a diferenciação no modo de avanço pode ser muito, muito mais rápida.
Agora faz sentido?
Quando aprendemos pela primeira vez o que é backpropagation, a reação é: “Oh, essa é apenas a regra da cadeia (chain rule)! Como demoramos tanto tempo para descobrir?”
Na época em que o backpropagation foi inventado, as pessoas não estavam muito focadas nas redes neurais feedforward. Também não era óbvio que as derivadas eram o caminho certo para treiná-las. Esses são apenas óbvios quando você percebe que pode calcular rapidamente derivadas. Houve uma dependência circular.
Treinar redes neurais com derivadas? Certamente você ficaria preso em mínimos locais. E obviamente seria caro computar todas essas derivadas. O fato é que só porque sabemos que essa abordagem funciona é que não começamos imediatamente a listar os motivos que provavelmente não funcionaria. Já sabemos que funciona, mas novas abordagens vem sendo propostas no avanço das pesquisas em Deep Learning e Inteligência Artificial.
Conclusão da Parte 1
O backpropagation também é útil para entender como as derivadas fluem através de um modelo. Isso pode ser extremamente útil no raciocínio sobre porque alguns modelos são difíceis de otimizar. O exemplo clássico disso é o problema do desaparecimento de gradientes em redes neurais recorrentes, que discutiremos mais diante neste livro.
Por fim, há uma lição algorítmica ampla a ser retirada dessas técnicas. Backpropagation e forward-mode differentiation usam um poderoso par de truques (linearização e programação dinâmica) para computar derivadas de forma mais eficiente do que se poderia imaginar. Se você realmente entende essas técnicas, pode usá-las para calcular com eficiência várias outras expressões interessantes envolvendo derivadas.
Mas este capítulo teve como objetivo apenas ajudá-lo a compreender o algoritmo, já que praticamente não existe documentação sobre isso em português. Falta ainda compreender como o backpropagation é aplicado no treinamento das redes neurais. Ansioso por isso? Então acompanhe o próximo capítulo!
Referências:
Me Salva! Cálculo – O que é uma derivada?
The Birth Of Graph Theory: Leonhard Euler And The Königsberg Bridge Problem
Learning representations by back-propagating errors
Calculus on Computational Graphs: Backpropagation
How the backpropagation algorithm works
Nota: parte das imagens usadas neste capítulo foram extraídas no excelente post (citado nas referências acima) de Christopher Olah, pesquisador de Machine Learning do Google Brain, e com a devida autorização do autor.

