Capítulo 43 – Camadas de Pooling em Redes Neurais Convolucionais
Além das camadas convolucionais que acabamos de descrever nos capítulos anteriores, as redes neurais convolucionais também contêm camadas de agrupamento (ou Pooling). Camadas de Pooling são geralmente usadas imediatamente após camadas convolucionais e o que fazem é simplificar as informações na saída da camada convolucional.
Vejamos o que são e como funcionam as Camadas de Pooling em Redes Neurais Convolucionais e na sequência vamos colocar todas as camadas juntas para compreender como funciona todo o processo nesta importante arquitetura de Deep Learning.
A Camada de Pooling
Uma camada de pooling recebe cada saída do mapa de características da camada convolucional e prepara um mapa de características condensadas. Por exemplo, cada unidade na camada de pooling pode resumir uma região de (digamos) 2 × 2 neurônios na camada anterior. Como um exemplo concreto, um procedimento comum para o pooling é conhecido como pool máximo (ou Max-Pooling). No Max-Pooling, uma unidade de pooling simplesmente gera a ativação máxima na região de entrada 2 × 2, conforme ilustrado no diagrama a seguir:

Note que, como temos 24 × 24 neurônios emitidos da camada convolucional, após o agrupamento, temos 12 × 12 neurônios.
Como mencionado acima, a camada convolucional geralmente envolve mais do que um único mapa de características. Aplicamos o Max-Pooling para cada mapa de recursos separadamente. Portanto, se houvesse três mapas de recursos, as camadas combinadas, convolutional e Max-Pooling, se pareceriam com:
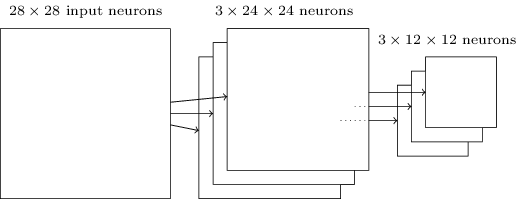
Podemos pensar em Max-Pooling como uma forma de a rede perguntar se um determinado recurso é encontrado em qualquer lugar de uma região da imagem. Em seguida, elimina a informação posicional exata. A intuição é que, uma vez que um recurso tenha sido encontrado, sua localização exata não é tão importante quanto sua localização aproximada em relação a outros recursos. Um grande benefício é que há muito menos recursos agrupados e, portanto, isso ajuda a reduzir o número de parâmetros necessários nas camadas posteriores. Genial, não?
O Max-Pooling não é a única técnica usada para o pooling. Outra abordagem comum é conhecida como Pooling L2. Aqui, em vez de tomar a ativação máxima de uma região 2 × 2 de neurônios, tomamos a raiz quadrada da soma dos quadrados das ativações na região 2 × 2. Embora os detalhes sejam diferentes, a intuição é semelhante ao agrupamento máximo: o Pooling L2 é uma maneira de condensar informações da camada convolucional. Na prática, ambas as técnicas têm sido amplamente utilizadas. E às vezes as pessoas usam outros tipos de operação de Pooling.
Se você estiver realmente tentando otimizar o desempenho, poderá usar dados de validação para comparar várias abordagens diferentes ao Pooling e escolher a abordagem que funciona melhor.
Juntando Tudo
Podemos agora juntar todas essas ideias para formar uma rede neural convolucional completa. É semelhante à arquitetura que estávamos estudando nos capítulos anteriores, mas tem a adição de uma camada de 10 neurônios de saída, correspondentes aos 10 valores possíveis para dígitos MNIST (‘0’, ‘1’, ‘2’, etc):
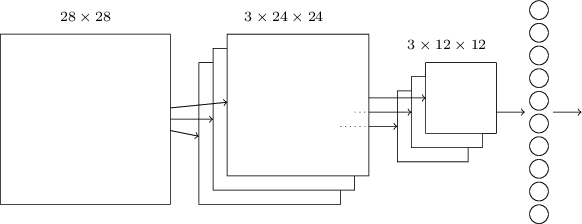
A rede começa com 28 × 28 neurônios de entrada (cada image de cada dígito do dataset MNIST tem 28 x 28 pixels), que são usados para codificar as intensidades de pixel para uma imagem no dataset MNIST. Este é então seguido por uma camada convolucional usando um campo receptivo local de 5 x 5 e três mapas de características. O resultado é uma camada de 3 × 24 × 24 neurônios ocultos. A próxima etapa é uma camada de Max-Pooling, aplicada a regiões 2 × 2, em cada um dos três mapas de recursos. O resultado é uma camada de 3 × 12 × 12 neurônios ocultos.
A camada final de conexões na rede é uma camada totalmente conectada. Ou seja, essa camada conecta todos os neurônios da camada de max-pooling a cada um dos 10 neurônios de saída. Essa arquitetura totalmente conectada é a mesma que usamos nos capítulos anteriores. Note, no entanto, que no diagrama acima, usei uma única seta, por simplicidade, em vez de mostrar todas as conexões. Claro, você pode facilmente imaginar as conexões.
Ou seja, temos uma rede composta de muitas unidades simples, cujos comportamentos são determinados por seus pesos e vieses. E o objetivo geral ainda é o mesmo: usar dados de treinamento para treinar os pesos e vieses da rede para que a rede faça um bom trabalho classificando os dígitos de entrada.
Em particular, assim como no início do livro, nós vamos treinar nossa rede usando descida estocástica do gradiente e retropropagação. Isso ocorre principalmente da mesma maneira que nos capítulos anteriores. No entanto, precisamos fazer algumas modificações no procedimento de retropropagação. A razão é que nossa derivação anterior da retropropagação foi para redes com camadas totalmente conectadas. Felizmente, é simples modificar a derivação para camadas convolucional e max-pooling.
Quer ver tudo isso funcionando em linguagem Python? Então não perca o próximo capítulo!
Referências:
Análise de Imagens com Inteligência Artificial
Don’t Decay the Learning Rate, Increase the Batch Size
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
A Comprehensive Guide to Convolutional Neural Networks
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

