Capítulo 22 – Regularização L1
Existem muitas técnicas de regularização além da Regularização L2 que vimos no capítulo anterior. De fato, tantas técnicas foram desenvolvidas que é difícil resumir todas elas. Neste e nos próximos dois capítulos, vamos descrever brevemente três outras abordagens para reduzir o overfitting: Regularização L1, Dropout e aumento artificial do tamanho do conjunto de treinamento. Não aprofundaremos tanto nessas técnicas como fizemos com a Regularização L2. Em vez disso, o objetivo é familiarizar você com as ideias principais e apreciar a diversidade de técnicas de regularização disponíveis.
Regularização L1
Nesta abordagem, modificamos a função de custo não regularizada, adicionando a soma dos valores absolutos dos pesos:
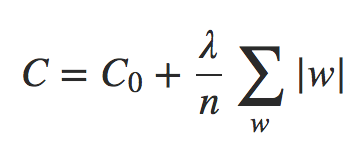
Equação 1
Intuitivamente, isso é semelhante à Regularização L2, penalizando grandes pesos e tendendo a fazer com que a rede prefira pequenos pesos. Naturalmente, o termo de Regularização L1 não é o mesmo que o termo de Regularização L2 e, portanto, não devemos esperar obter exatamente o mesmo comportamento. Vamos tentar entender como o comportamento de uma rede treinada usando a Regularização L1 difere de uma rede treinada usando a Regularização L2.
Para fazer isso, vejamos as derivadas parciais da função de custo. A partir da fórmula anterior obtemos:
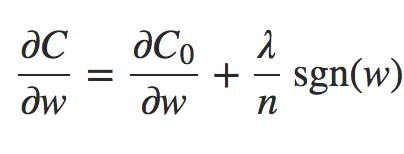
Equação 2
onde sgn(w) é o sinal de w, isto é, +1 se w é positivo e −1 se w é negativo. Usando essa expressão, podemos facilmente modificar a retropropagação (backpropagation) para fazer a descida de gradiente estocástica usando a Regularização L1. A regra de atualização resultante para uma rede regularizada L1 é:
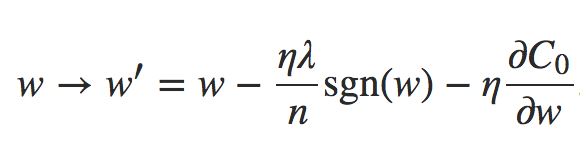
Equação 3 – Regra de atualização L1
onde, como de costume, podemos estimar ∂C0/∂w usando uma média de mini-lote, se desejarmos. Compare isso com a regra de atualização para a Regularização L2:
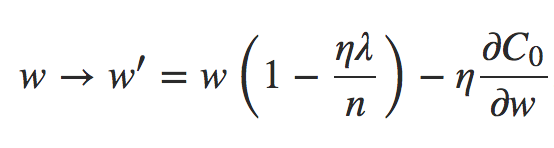
Equação 4 – Regra de atualização L2
Em ambas as expressões, o efeito da regularização é diminuir os pesos. Isso está de acordo com a nossa intuição de que ambos os tipos de regularização penalizam grandes pesos. Mas a maneira como os pesos diminuem é diferente. Na Regularização L1, os pesos diminuem em uma quantidade constante para 0. Na Regularização L2, os pesos diminuem em um valor proporcional a w. E assim, quando um peso específico tem uma grande magnitude, a Regularização L1 reduz o peso muito menos do que a Regularização L2. Em contraste, quando |w| é pequena, a Regularização L1 reduz o peso muito mais do que a Regularização L2. O resultado é que a Regularização L1 tende a concentrar o peso da rede em um número relativamente pequeno de conexões de alta importância, enquanto os outros pesos são direcionados para zero.
Mas há ainda um pequeno detalhe na discussão acima. A derivada parcial ∂C/∂w não é definida quando w = 0. A razão é que a função |w| tem um “canto” agudo em w = 0 e, portanto, não é diferenciável nesse ponto. Tudo bem, no entanto. O que faremos é aplicar a regra usual (não regularizada) para descida de gradiente estocástica quando w = 0. Isso ajuda a resolver a questão – intuitivamente, o efeito da regularização é diminuir os pesos e, obviamente, não pode reduzir um peso que já é 0. Para colocá-lo com mais precisão, usaremos as Equações (2) e (3) com a convenção que sgn(0) = 0. Isso dá uma regra legal e compacta para se fazer uma descida gradiente estocástica com Regularização L1.
Agora vamos para o Dropout, no próximo capítulo!
Referências:
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning
Pattern Recognition and Machine Learning

