Capítulo 32 – Como Uma Rede Neural Artificial Encontra a Aproximação de Uma Função
Este é um capítulo muito importante para compreender como as redes neurais realmente funcionam e Como Uma Rede Neural Artificial Encontra a Aproximação de Uma Função. Acompanhe a explicação passo a passo analisando cada um dos gráficos apresentados.
Mas antes de explicar porque o teorema da universalidade é verdadeiro, quero mencionar duas advertências a esta declaração informal: “uma rede neural pode computar qualquer função”, que vimos no capítulo anterior.
Primeiro, isso não significa que uma rede possa ser usada para calcular exatamente qualquer função. Em vez disso, podemos obter uma aproximação que seja tão boa quanto desejamos. Aumentando o número de neurônios ocultos, podemos melhorar a aproximação. Por exemplo, anteriormente ilustramos uma rede computando alguma função f(x) usando três neurônios ocultos. Para a maioria das funções, apenas uma aproximação de baixa qualidade será possível usando três neurônios ocultos. Ao aumentar o número de neurônios ocultos (digamos, para cinco), podemos obter uma melhor aproximação:
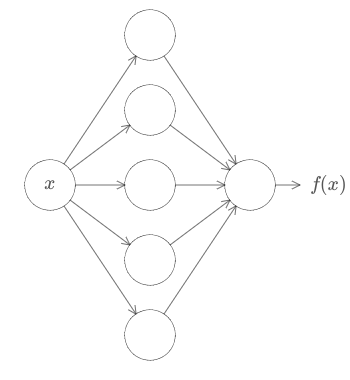
E podemos melhorar ainda mais aumentando o número de neurônios ocultos.
Para tornar esta afirmação mais precisa, suponha que tenhamos uma função f(x) que gostaríamos de computar com alguma precisão desejada ϵ > 0. A garantia é que usando neurônios ocultos suficientes sempre podemos encontrar uma rede neural cuja saída g(x) satisfaça | g(x) − f(x) | < ϵ, para todas as entradas x. Em outras palavras, a aproximação será boa dentro da precisão desejada para cada entrada possível.
A segunda ressalva é que a classe de funções que podem ser aproximadas da maneira descrita são as funções contínuas. Se uma função é descontínua, isto é, faz saltos bruscos e repentinos, então, em geral, não será possível aproximar usando uma rede neural. Isso não é surpreendente, já que nossas redes neurais calculam funções contínuas de sua entrada.
No entanto, mesmo que a função que realmente gostaríamos de computar fosse descontínua, muitas vezes a aproximação contínua é boa o suficiente. Se é assim, então podemos usar uma rede neural. Na prática, isso geralmente não é uma limitação importante.
Em suma, uma afirmação mais precisa do teorema da universalidade é que redes neurais com uma única camada oculta podem ser usadas para aproximar qualquer função contínua a qualquer precisão desejada. Neste e no próximo capítulo, vamos provar uma versão desse resultado.
Universalidade Com Uma Entrada e Uma Saída
Para entender por que o teorema da universalidade é verdadeiro, vamos começar entendendo como construir uma rede neural que se aproxima de uma função com apenas uma entrada e uma saída:

Este é o cerne do problema da universalidade. Uma vez que entendemos esse caso especial, é realmente fácil estender para funções com muitas entradas e muitas saídas (tema do próximo capítulo).
Para construir um insight sobre como construir uma rede para calcular f, vamos começar com uma rede contendo apenas uma camada oculta, com dois neurônios ocultos e uma camada de saída contendo um único neurônio de saída:
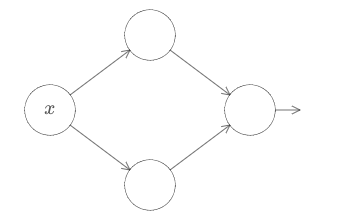
Para ter uma ideia de como funcionam os componentes da rede, vamos nos concentrar no neurônio oculto superior. No diagrama abaixo, aumentando o valor de w, podemos ver imediatamente como a função computada pelo neurônio oculto superior muda:
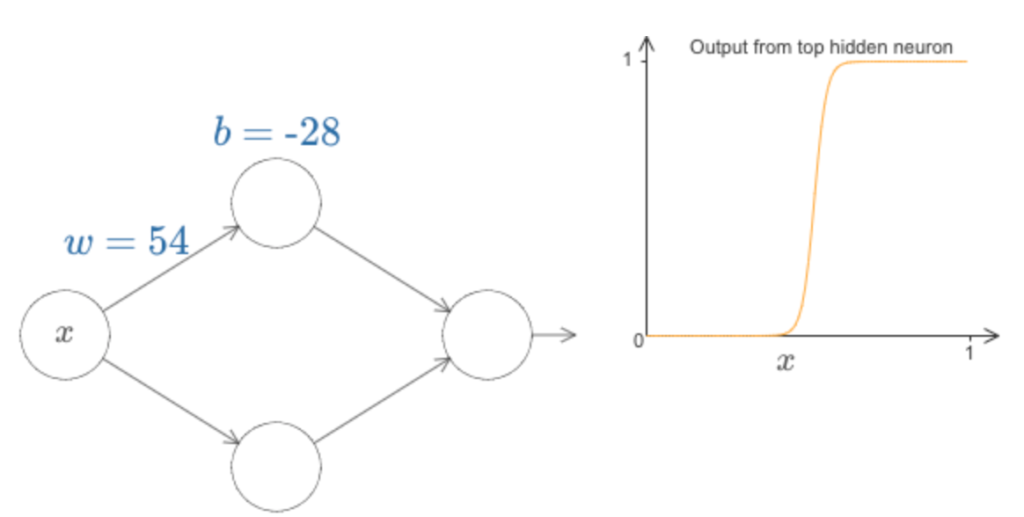
Como aprendemos anteriormente no livro, o que está sendo computado pelo neurônio oculto é σ(wx + b), onde σ(z) ≡ 1 / (1 + e^-z) é a função sigmóide. Até agora, fizemos uso frequente dessa forma algébrica. Mas, para a prova da universalidade, obteremos mais discernimento ignorando inteiramente a álgebra e, em vez disso, manipulando e observando a forma mostrada no gráfico. Isso não apenas nos dará uma ideia melhor do que está acontecendo, mas também nos dará uma prova de universalidade que se aplica a outras funções de ativação que não a função sigmóide.
Para começar esta prova, podemos aumentar o bias, b, no diagrama acima. Você verá que, conforme o bias aumenta, o gráfico se move para a esquerda, mas sua forma não muda.
Em seguida, podemos diminuir o viés (bias). Você verá que conforme o viés diminui, o gráfico se move para a direita, mas, novamente, sua forma não muda. Em seguida, diminuímos o peso para cerca de 2 ou 3. Você verá que à medida que diminui o peso, a curva se alarga. Talvez seja necessário alterar o bias também, para manter a curva no quadro.
Finalmente, aumentamos o peso acima de w = 100. A curva fica mais íngreme, até que, eventualmente, ela começa a parecer uma função de passo (Step Function). A imagem a seguir mostra como deve ser resultado:
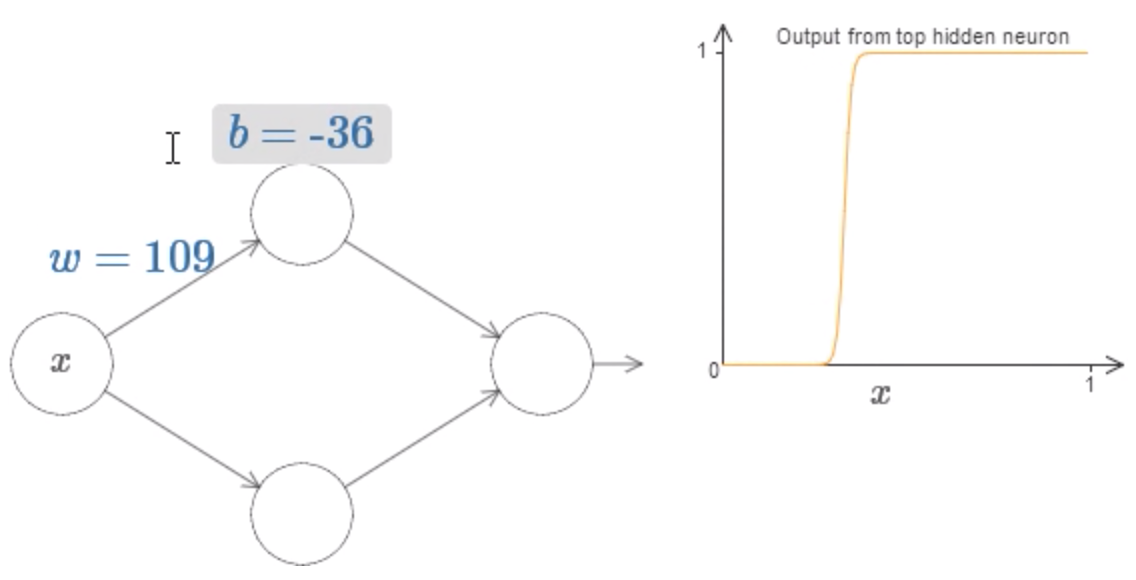
Podemos simplificar um pouco nossa análise aumentando o peso para que a saída realmente seja uma Step Function, para uma aproximação muito boa. Abaixo eu plotei a saída do neurônio oculto superior quando o peso é w = 999.
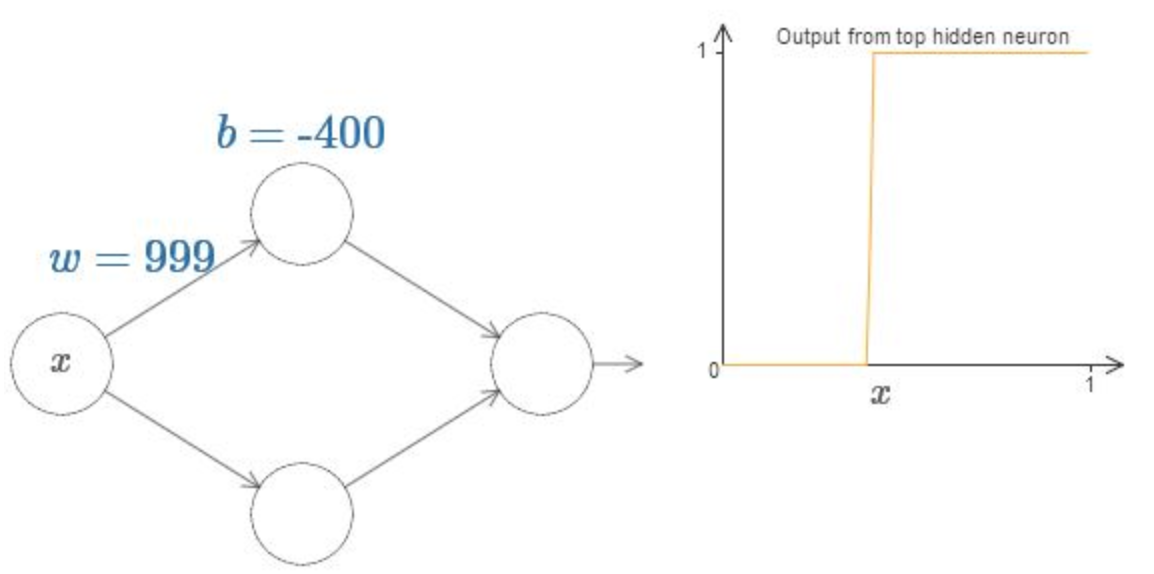
Na verdade, é um pouco mais fácil trabalhar com funções step do que com funções gerais sigmóides. A razão é que, na camada de saída, somamos contribuições de todos os neurônios ocultos. É fácil analisar a soma de várias funções step, mas é mais difícil pensar sobre o que acontece quando você adiciona um monte de curvas em forma de sigmóide.
E assim torna as coisas muito mais fáceis de assumir que nossos neurônios ocultos estão emitindo funções step. Mais concretamente, fazemos isso fixando o peso w como sendo um valor muito grande e, em seguida, definindo a posição da etapa modificando o bias. É claro que tratar a saída como uma função step é uma aproximação, mas é uma aproximação muito boa e, por enquanto, vamos tratá-la como exata. Voltarei mais tarde para discutir o impacto dos desvios dessa aproximação.
Em que valor de x a etapa ocorre? Em outras palavras, como a posição da etapa depende do peso e do viés?
Para responder a essa pergunta, podemos modificar o peso e o viés no diagrama acima. Você consegue descobrir como a posição da etapa depende de w e b. Com um pouco de trabalho, você deve ser capaz de se convencer de que a posição da etapa é proporcional a b e inversamente proporcional a w.
Na verdade, a etapa está na posição s = −b / w, como você pode ver modificando o peso e o bias no diagrama a seguir:
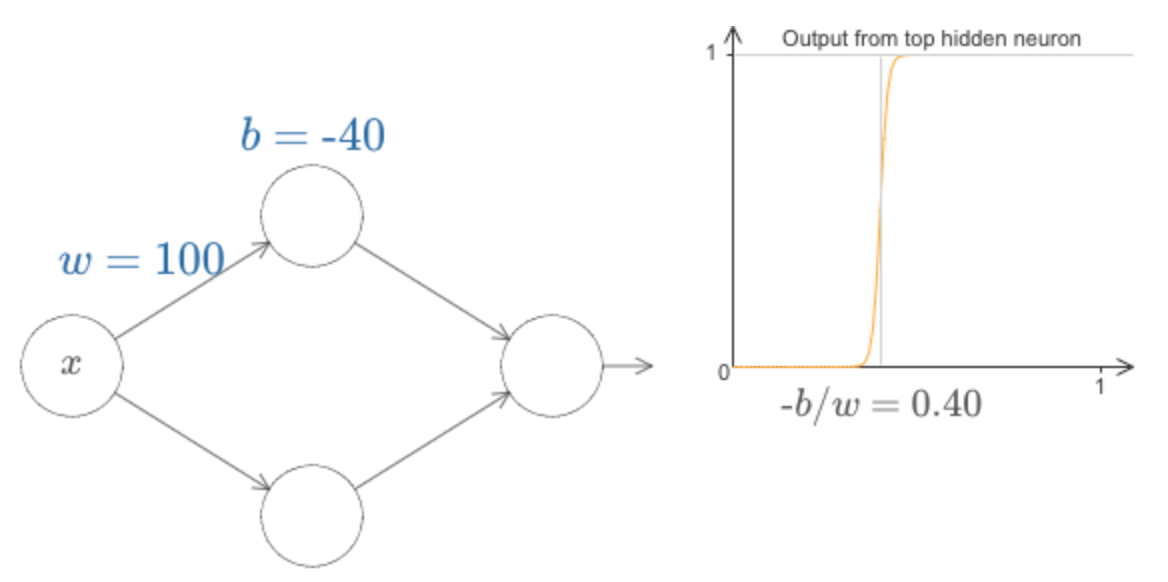
Isso simplificará muito nossas vidas para descrever os neurônios ocultos usando apenas um único parâmetro, s, que é a posição do passo, s = −b / w.
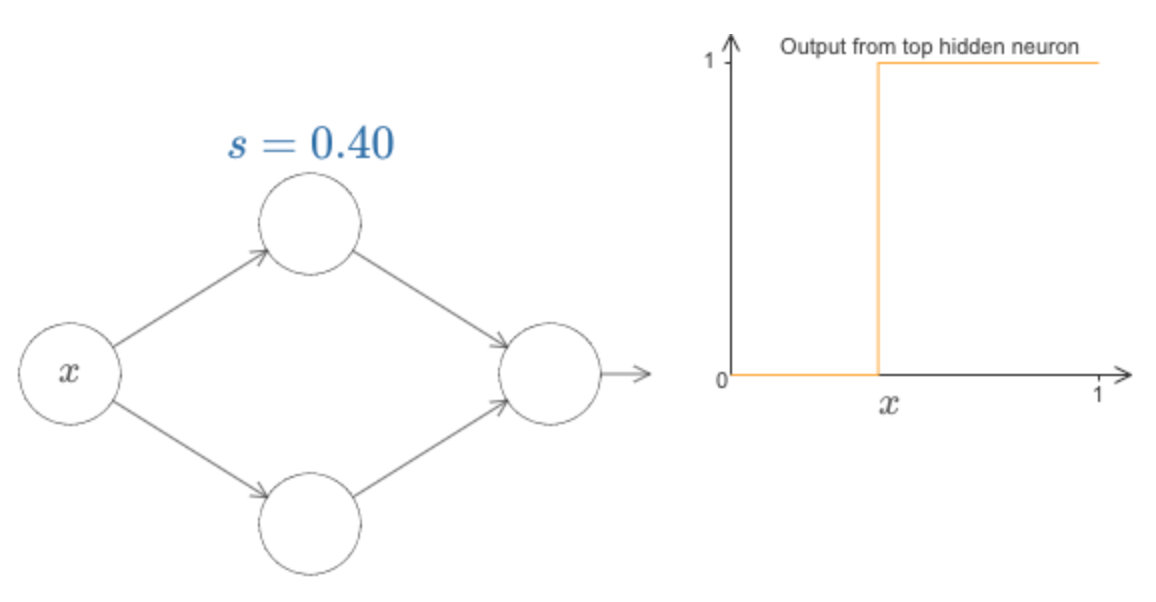
Como mencionado acima, nós implicitamente definimos o peso w na entrada como um valor grande – grande o suficiente para que a função de passo seja uma boa aproximação. Podemos facilmente converter um neurônio parametrizado dessa maneira de volta ao modelo convencional, escolhendo o viés b = −ws.
Até agora, nos concentramos na saída apenas do neurônio oculto superior. Vamos dar uma olhada no comportamento de toda a rede. Em particular, vamos supor que os neurônios ocultos estejam computando funções de passos parametrizadas pelos pontos de degrau s1 (neurônio superior) e s2 (neurônio de baixo). E eles terão os respectivos pesos de saída w1 e w2. Aqui está a rede:
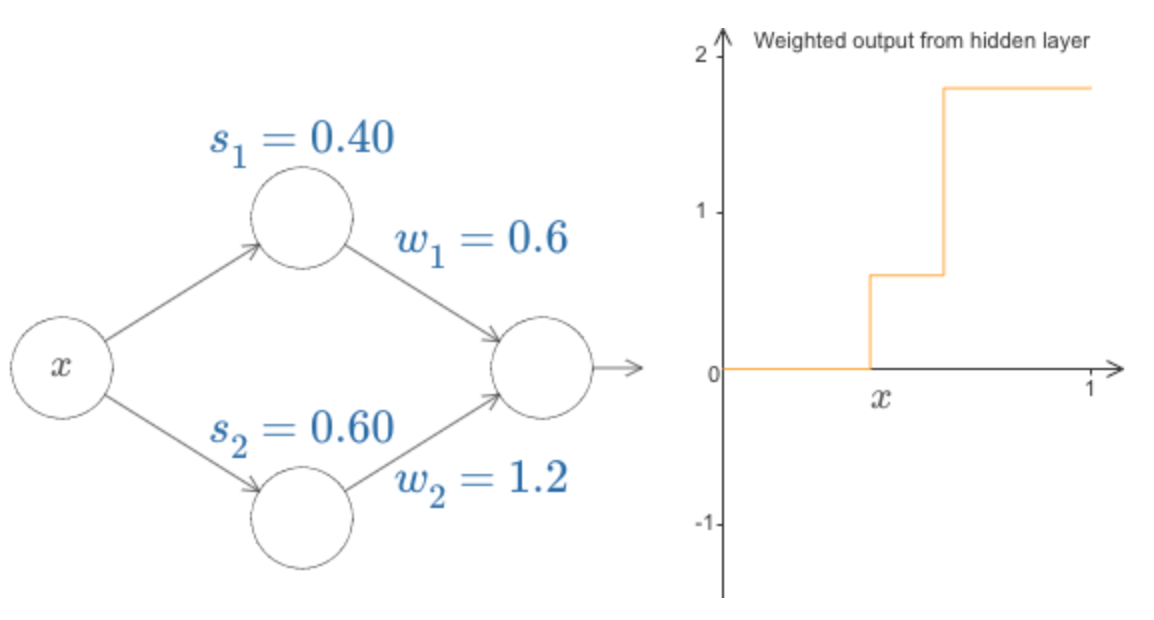
O que está sendo plotado à direita é a saída ponderada w1a1 + w2a2 da camada oculta. Aqui, a1 e a2 são as saídas dos neurônios ocultos superior e inferior, respectivamente. Essas saídas são frequentemente conhecidas como ativações dos neurônios.
Podemos aumentar ou diminuir o ponto de passo s1 do neurônio oculto superior e isso nos dá uma ideia de como isso altera a saída ponderada da camada oculta. Vale a pena entender o que acontece quando o s1 passa do s2. Você verá que o gráfico muda de forma quando isso acontece, já que nos movemos de uma situação em que o neurônio oculto superior é o primeiro a ser ativado para uma situação em que o neurônio oculto na parte inferior é o primeiro a ser ativado.
Da mesma forma, podemos manipular o ponto de passo s2 do neurônio oculto na parte inferior e ter uma ideia de como isso altera a saída combinada dos neurônios ocultos.
Finalmente, podemos definir w1 como 0.8 e w2 como −0.8. Você recebe uma função “bump”, que começa no ponto s1, termina no ponto s2 e tem a altura 0.8. Por exemplo, a saída ponderada pode ser assim:
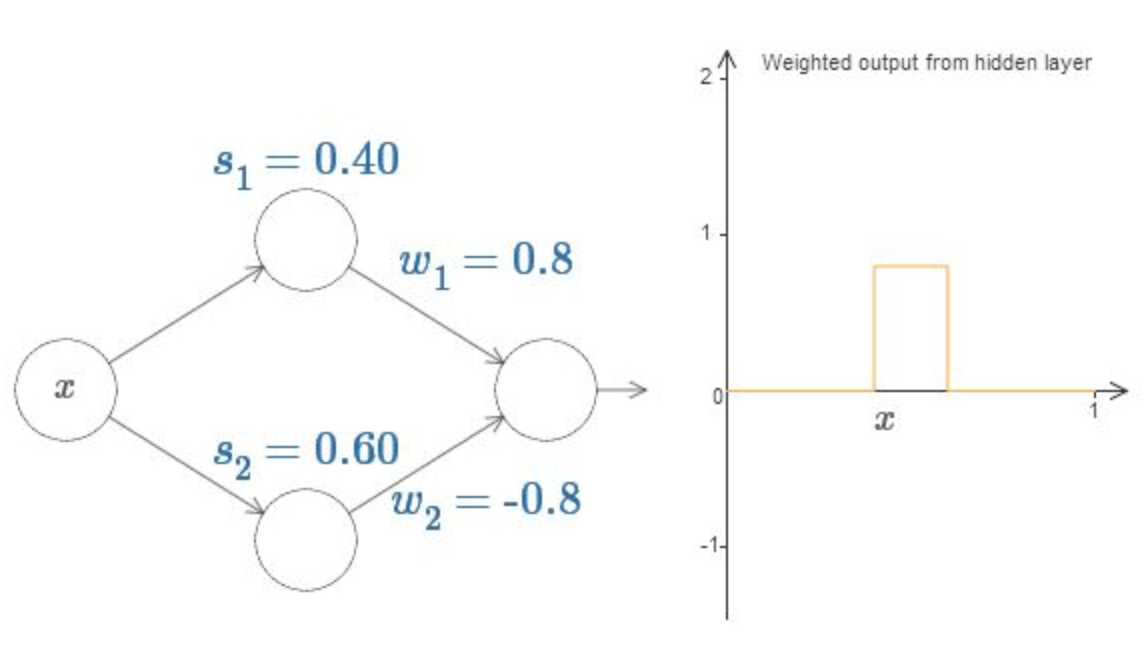
Claro, podemos redimensionar o bump para ter qualquer altura. Vamos usar um único parâmetro, h, para indicar a altura. Para reduzir a confusão, também removerei as notações “s1 = …” e “w1 = …”.
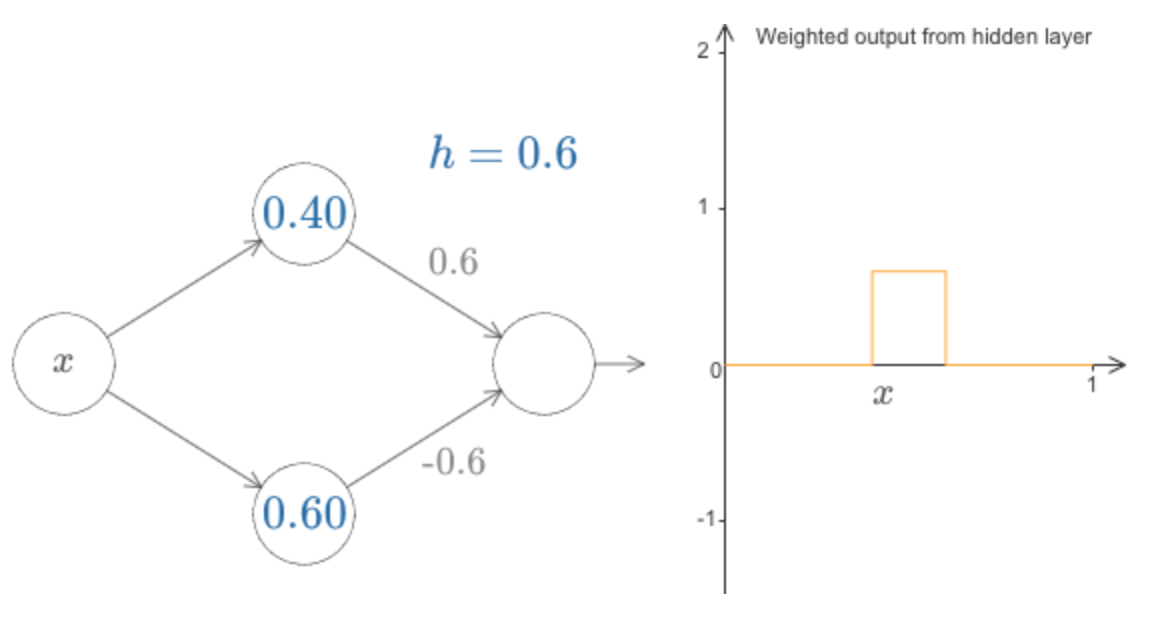
Podemos alterar o valor de h para cima e para baixo, para ver como a altura do bump muda.
Você notará, a propósito, que estamos usando nossos neurônios de uma forma que pode ser pensada não apenas em termos gráficos, mas em termos de programação mais convencionais, como uma espécie de declaração if-then-else, por exemplo:

Na maior parte eu vou ficar com o ponto de vista gráfico. Mas, no que se segue, às vezes você pode achar útil trocar pontos de vista e pensar sobre as coisas em termos de se-então-senão (uma das bases da programação convencional).
Podemos usar o nosso truque de fazer bump para obter dois solavancos, colando dois pares de neurônios ocultos na mesma rede:
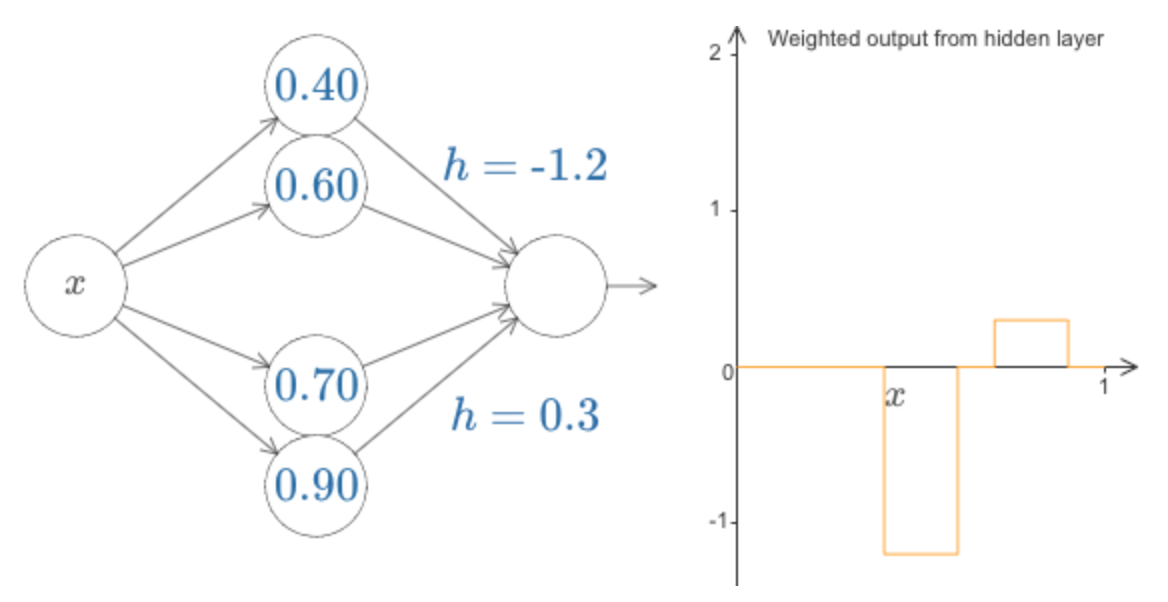
Eu suprimi os pesos aqui, simplesmente escrevendo os valores h para cada par de neurônios ocultos.
De maneira mais geral, podemos usar essa ideia para obter o máximo de picos que quisermos, de qualquer altura. Em particular, podemos dividir o intervalo [0,1] em um número grande, N, de subintervalos, e usar N pares de neurônios ocultos para configurar picos de qualquer altura desejada. Vamos ver como isso funciona para N = 5. Desculpa pela a complexidade do diagrama abaixo (eu poderia esconder a complexidade abstraindo mais, mas acho que vale a pena colocar um pouco de complexidade, para obter uma ideia mais concreta de como essas redes funciona):
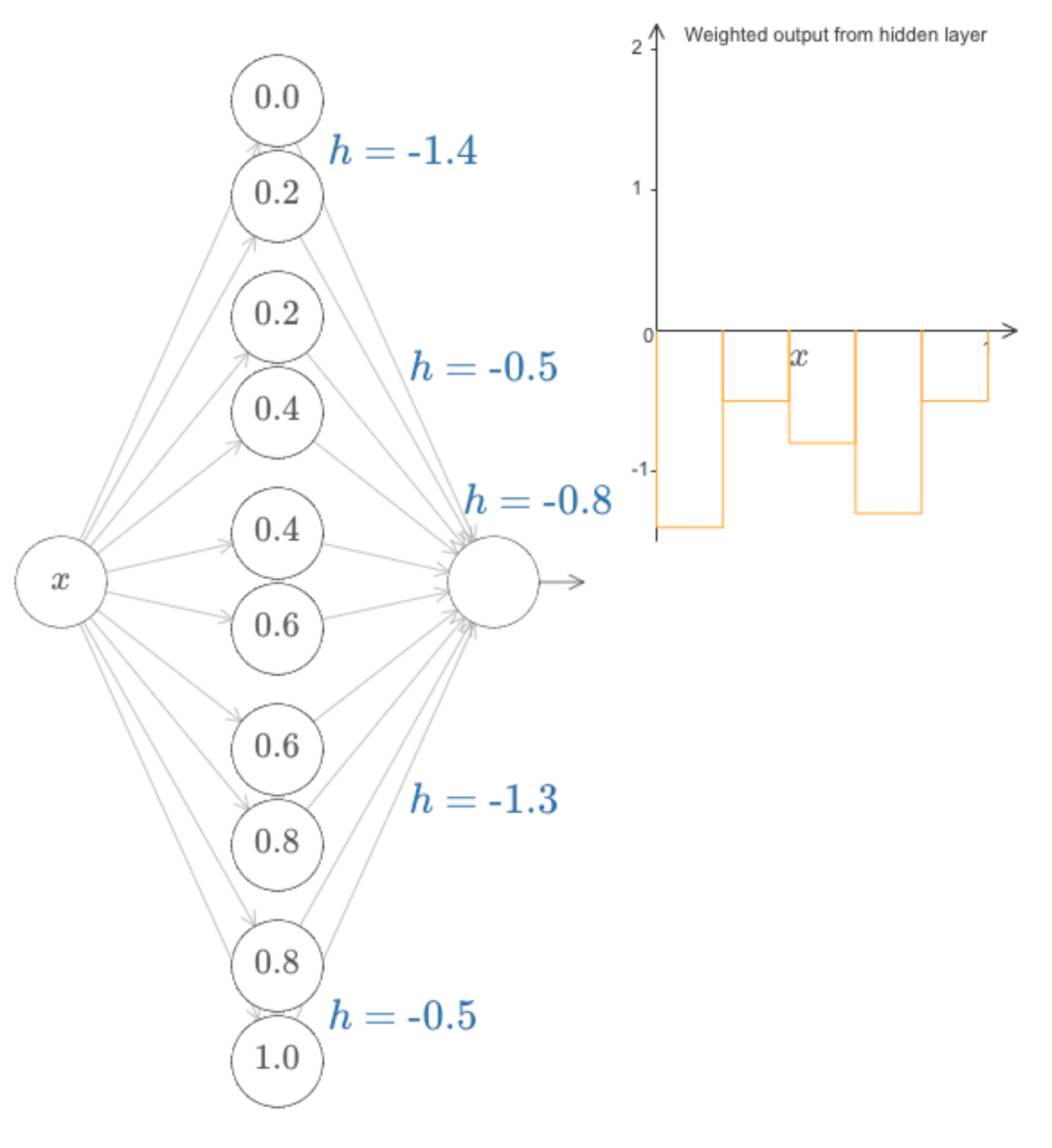
Você pode ver que existem cinco pares de neurônios ocultos. Os pontos escalonados para os respectivos pares de neurônios são 0,1 / 5, depois 1 / 5,2 / 5 e assim por diante, para 4 / 5,5 / 5. Esses valores são fixos – eles fazem com que tenhamos cinco saliências uniformemente espaçadas no gráfico.
Cada par de neurônios tem um valor de h associado a ele. Lembre-se, as conexões saídas dos neurônios têm pesos h e −h (não marcados). Ao alterar os pesos de saída, estamos realmente projetando a função!
Conforme alteramos as alturas, é possível ver a mudança correspondente nos valores h. E há também uma mudança nos pesos de saída correspondentes, que são + h e −h.
Em outras palavras, podemos manipular diretamente a função que aparece no gráfico à direita e ver isso refletido nos valores h à esquerda.
Mas aqui consideramos uma entrada e uma saída, o que é bem simples. Com múltiplas entradas o conceito é basicamente o mesmo, mas iremos discutir as particularidades nos próximos capítulos, quando mergulharmos nas redes neurais profundas. Até lá.
Referências:
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning (material utilizado com autorização do autor)
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

