Capítulo 42 – Compartilhamento de Pesos em Redes Neurais Convolucionais
Vamos continuar estudando Deep Learning e investigar como funciona o Compartilhamento de Pesos em Redes Neurais Convolucionais.
Já dissemos que cada neurônio tem um viés e pesos 5 × 5 conectados ao seu campo receptivo local. O que eu não mencionamos é que vamos usar os mesmos pesos e vieses para cada um dos 24 × 24 neurônios ocultos. Em outras palavras, para o neurônio oculto, a saída é:
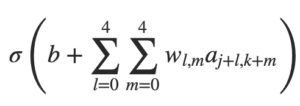
Isso significa que todos os neurônios da primeira camada oculta detectam exatamente o mesmo recurso, apenas em locais diferentes na imagem de entrada. Para entender porque isso faz sentido, suponha que os pesos e os vieses sejam tais que o neurônio oculto possa escolher, digamos, uma borda vertical em um campo receptivo local específico. Essa habilidade também é útil em outros lugares da imagem. Por isso, é útil aplicar o mesmo detector de recursos em toda a imagem. Para colocar esse conceito em termos um pouco mais abstratos, as redes convolucionais são bem adaptadas à invariância da transalação das imagens: girar uma foto de um gato 90 graus, ainda faz dela a imagem de um gato, embora os pixels agora estejam organizados de forma diferente.
Por esse motivo, às vezes chamamos o mapa da camada de entrada para a camada oculta de um mapa de recursos. Chamamos os pesos que definem o mapa de recursos de pesos compartilhados. E nós chamamos o viés usado no mapa de recursos desta maneira de viés compartilhado. Os pesos e vieses compartilhados costumam definir um kernel ou filtro. Na literatura, as pessoas às vezes usam esses termos de maneiras ligeiramente diferentes e mais a frente veremos alguns exemplos concretos.
A estrutura de rede que descrevemos até agora pode detectar apenas um único tipo de recurso localizado. Para fazer reconhecimento de imagem, precisaremos de mais de um mapa de recursos. E assim, uma camada convolucional completa consiste em vários mapas de recursos, diferentes:
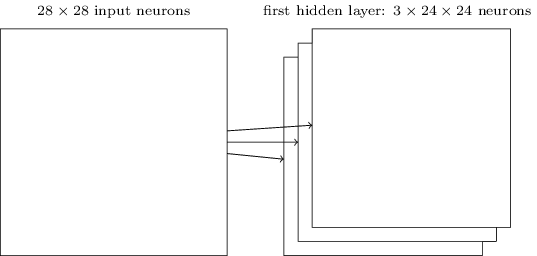
No exemplo mostrado acima, existem 3 mapas de recursos. Cada mapa de recursos é definido por um conjunto de pesos compartilhados de 5 × 5 e um único viés compartilhado. O resultado é que a rede pode detectar três tipos diferentes de recursos, sendo cada recurso detectável em toda a imagem.
No exemplo temos apenas 3 mapas de recursos, para manter o diagrama acima simples. No entanto, na prática, as redes convolucionais podem usar mais (e talvez muito mais) mapas de recursos. Uma das primeiras redes convolucionais, a LeNet-5, usou 6 mapas de recursos, cada um associado a um campo receptivo local 5 × 5, para reconhecer dígitos MNIST. Portanto, o exemplo ilustrado acima está bem próximo do LeNet-5. Nos exemplos que desenvolveremos mais adiante neste livro, usaremos camadas convolucionais com 20 e 40 mapas de recursos. Vamos dar uma olhada rápida em alguns dos recursos que são aprendidos:

As 20 imagens correspondem a 20 diferentes mapas de recursos (ou filtros ou kernels). Cada mapa é representado como uma imagem 5 × 5, correspondendo aos pesos 5 × 5 no campo receptivo local. Blocos mais brancos significam um peso menor (normalmente, mais negativo), portanto, o mapa de recursos responde menos aos pixels de entrada correspondentes. Blocos mais escuros significam um peso maior, portanto, o mapa de recursos responde mais aos pixels de entrada correspondentes. Muito grosso modo, as imagens acima mostram o tipo de características que a camada convolucional responde.
Então, o que podemos concluir desses mapas de recursos? Está claro que há estrutura espacial aqui além do que esperamos ao acaso: muitos dos recursos têm claras sub-regiões de luz e escuridão. Isso mostra que nossa rede realmente está aprendendo coisas relacionadas à estrutura espacial. No entanto, além disso, é difícil ver o que esses detectores de recursos estão aprendendo. De fato, agora há muito trabalho para entender melhor os recursos aprendidos pelas redes convolucionais. Se você estiver interessado em acompanhar esse trabalho, sugiro começar com o artigo Visualizando e Compreendendo Redes Convolucionais de Matthew Zeiler e Rob Fergus.
Uma grande vantagem do compartilhamento de pesos e vieses é que ele reduz bastante o número de parâmetros envolvidos em uma rede convolucional. Para cada mapa de recursos, precisamos de 5 × 5 = 25 pesos compartilhados, além de um único viés compartilhado. Portanto, cada mapa de recursos requer 26 parâmetros. Se temos 20 mapas de recursos, um total de 20 × 26 = 520 parâmetros define a camada convolucional. Em comparação, suponhamos que tivéssemos uma primeira camada totalmente conectada, com 784 = 28 × 28 neurônios de entrada e relativamente modestos 30 neurônios ocultos, como usamos em muitos dos exemplos anteriores no livro. Isso é um total de 784 × 30 pesos, além de um extra de 30 vieses, para um total de 23.550 parâmetros. Em outras palavras, a camada totalmente conectada teria mais de 40 vezes mais parâmetros que a camada convolucional.
É claro que não podemos fazer uma comparação direta entre o número de parâmetros, já que os dois modelos são diferentes em termos essenciais. Mas, intuitivamente, parece provável que o uso de invariância de tradução pela camada convolucional reduza o número de parâmetros necessários para obter o mesmo desempenho que o modelo totalmente conectado. Isso, por sua vez, resultará em um treinamento mais rápido para o modelo convolucional e, em última análise, nos ajudará a construir redes profundas usando camadas convolucionais.
A propósito, o nome convolucional vem do fato de que a operação na equação mostrada no início deste capítulo é às vezes conhecida como uma convolução. Um pouco mais precisamente, as pessoas às vezes escrevem essa equação como a1 = σ (b + w ∗ a0), onde a1 denota o conjunto de ativações de saída de um mapa de recursos, a0 é o conjunto de ativações de entrada e ∗ é chamado de operação de convolução.
No próximo capítulo estudaremos as camadas de Pooling, outro “segredo” por trás das Redes Neurais Convolucionais e então estaremos prontos para colocar tudo isso junto.
Referências:
Análise de Imagens com Inteligência Artificial
Don’t Decay the Learning Rate, Increase the Batch Size
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
A Comprehensive Guide to Convolutional Neural Networks
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

