Capítulo 70 – Deep Q-Network e Processos de Decisão de Markov

Nos capítulos anteriores estudamos os fundamentos do Aprendizado Por Reforço. Agora podemos subir mais alguns degraus e estudar uma evolução dessa fascinante técnica de aprendizado de máquina que une Deep Learning e Aprendizado Por Reforço: Deep Q-Network.

Acompanhe a leitura com atenção e na próxima aula traremos uma aplicação prática desse modelo de aprendizagem profunda.

O Processo

O processo de Q-Learning cria uma matriz (tabela) exata para o agente a qual ele “consulta” para maximizar sua recompensa a longo prazo durante seu aprendizado. Embora essa abordagem não seja errada por si só, é prática apenas para ambientes muito pequenos e rapidamente perde a viabilidade quando o número de estados e ações no ambiente aumenta.

A solução para o problema acima vem da constatação de que os valores na matriz têm apenas importância relativa, ou seja, os valores têm importância apenas em relação aos outros valores. Assim, esse pensamento nos leva a Deep Q-Network, que usa uma rede neural profunda para aproximar os valores. Essa aproximação de valores não prejudica desde que a importância relativa seja preservada. Ou seja, substituímos a Q Table no processo Q-Learning por um modelo de Deep Learning para o aprendizado dos valores Q. Por isso Deep Q-Network também é chamada de Deep Q-Learning.

A etapa básica de trabalho da Deep Q-Network é que o estado inicial seja alimentado na rede neural e retorne o valor Q de todas as ações possíveis, como na saída.

A diferença entre Q-Learning e Deep Q-Learning pode ser ilustrada da seguinte maneira:

Q-learning Usa uma Q Matrix (ou Q Table)

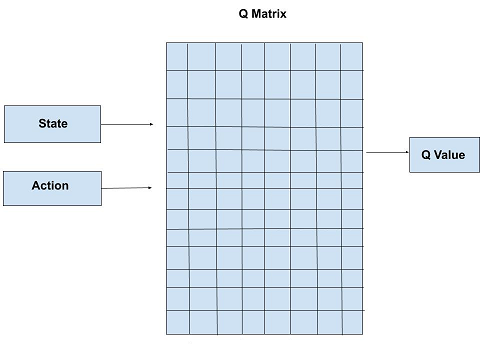
Deep Q-learning substitui a Q Matrix por uma rede neural profunda (Deep Learning):

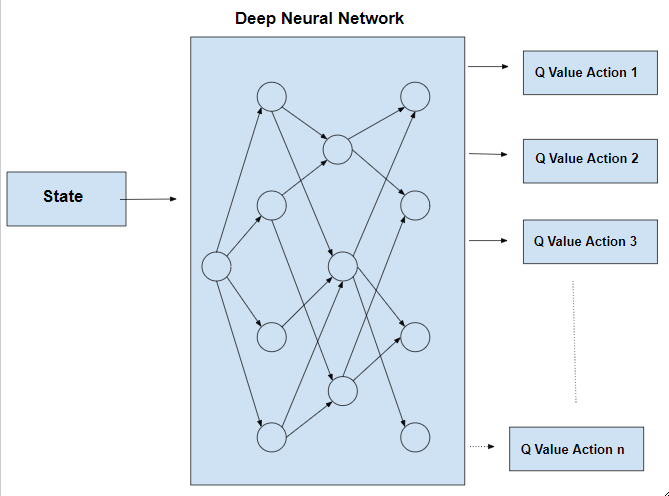
Vamos compreender as vantagens em usar Dep Q-Learning.

Definindo o Mundo

Uma tarefa de aprendizado por reforço é o treinamento de um agente que interage com seu ambiente. O agente faz a transição entre diferentes cenários do ambiente, chamados de estados, executando ações. As ações, em troca, geram recompensas, que podem ser positivas, negativas ou zero. O único objetivo do agente é maximizar a recompensa total que ele recebe sobre um episódio, que é tudo o que acontece entre um estado inicial e um estado terminal. Por isso, reforçamos o agente para executar determinadas ações, oferecendo-lhe recompensas positivas, e afastando-o de outras ações, fornecendo-lhe recompensas negativas. É assim que um agente aprende a desenvolver uma estratégia ou política.

Tome o Super Mario como exemplo: Mario é o agente que interage com o mundo (o ambiente). Os estados são exatamente o que vemos na tela, e um episódio é um nível: o estado inicial é como o nível começa e o estado terminal é como o nível termina, se o concluímos ou perecemos enquanto tentávamos. As ações avançam, retrocedem, saltam, etc. As recompensas são dadas dependendo do resultado das ações: quando Mario coleta moedas ou bônus, recebe uma recompensa positiva e, quando cai ou é atingido por um inimigo, recebe uma recompensa negativa . Quando Mario apenas anda em frente, a recompensa que recebe é zero, como se dissesse “você não fez nada de especial”.

Mas há um problema aqui: para poder receber recompensas, algumas ações “não especiais” são necessárias – é preciso caminhar em direção às moedas antes de poder recebê-las. Portanto, um agente deve aprender a lidar com recompensas adiadas, aprendendo a vinculá-las às ações que realmente as causaram. Essa é a característica mais fascinante no aprendizado por reforço.

Processos de Decisão de Markov

Cada estado em que o agente se encontra é uma conseqüência direta do estado anterior e da ação escolhida. O estado anterior também é uma consequência direta do que veio antes dele, e assim por diante até chegarmos ao estado terminal. Cada uma dessas etapas, e sua ordem, retém informações sobre o estado atual – e, portanto, têm efeito direto sobre qual ação o agente deve escolher a seguir. Mas há um problema óbvio aqui: quanto mais avançamos, mais informações o agente precisa para salvar e processar a cada passo necessário. Isso pode facilmente chegar ao ponto em que é simplesmente inviável realizar cálculos.

Para resolver isso, assumimos que todos os estados são Markov; isto é – assumimos que qualquer estado depende unicamente do estado que veio antes dele e da transição desse estado para o atual (a ação executada e a recompensa dada). Vamos ver um exemplo – veja estes dois jogos Tic Tac Toe (o famoso Jogo da Velha):

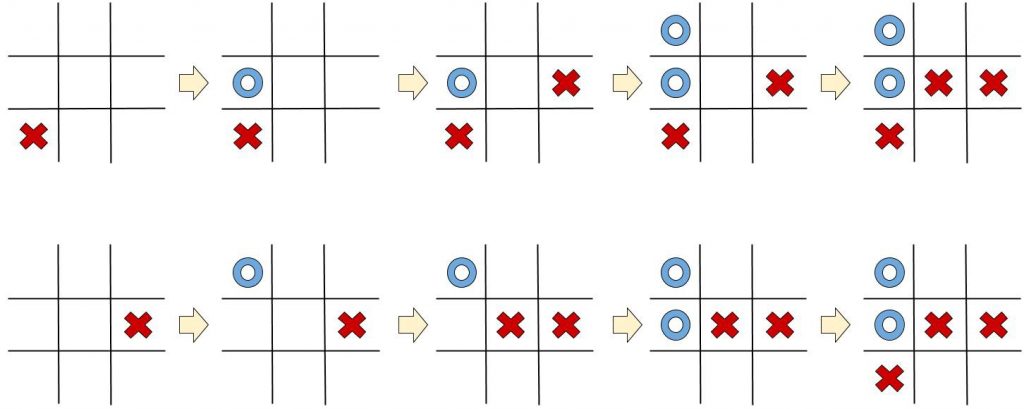
Ambos os jogos atingiram o mesmo estado, mas de maneiras diferentes. Ainda assim, em ambos os casos, o jogador azul deve capturar a célula superior direita, ou ele perderá. Tudo o que precisávamos para determinar esse estado era o último estado, nada mais.

É importante lembrar que, ao usar a suposição de Markov, dados estão sendo perdidos – em jogos complexos como Chess ou Go, a ordem dos movimentos pode ter algumas informações implícitas sobre a estratégia ou o modo de pensar do oponente. Ainda assim, a suposição de Markov é fundamental quando se tenta calcular estratégias de longo prazo.

A Equação de Bellman

Vamos seguir em frente e desenvolver nossa primeira estratégia. Considere o caso mais simples: suponha que já sabemos qual é a recompensa esperada para cada ação em cada etapa. Como vamos escolher uma ação neste caso? Simplesmente – escolheremos a sequência de ações que eventualmente gerará a maior recompensa. Essa recompensa cumulativa que receberemos é frequentemente referida como Q Value (uma abreviação de Quality Value) e podemos formalizar matematicamente nossa estratégia como:

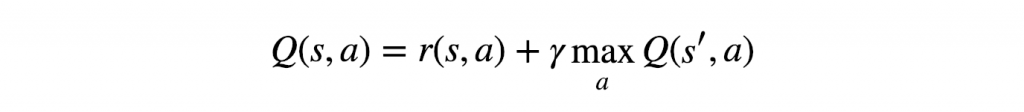
A equação acima afirma que o valor Q produzido por estar no estado s e selecionar a ação a é a recompensa imediata recebida, r (s, a), mais o valor Q mais alto possível do estado s’ (que é o estado em que chegamos depois de executar a ação a dos estados). Receberemos o valor Q mais alto de s’ escolhendo a ação que maximiza o valor Q. Também apresentamos γ, geralmente chamado de fator de desconto, que controla a importância das recompensas de longo prazo versus as imediatas.

Essa equação é conhecida como Equação de Bellman, e sua página na Wikipedia fornece uma explicação abrangente de sua derivação matemática. Essa equação elegante é bastante poderosa e é muito útil devido a duas características importantes:

Enquanto ainda mantemos as suposições dos estados de Markov, a natureza recursiva da Equação de Bellman permite que as recompensas dos estados futuros se propaguem para estados passados longínquos.
Não é necessário saber realmente quais são os verdadeiros valores Q quando começamos; Desde a sua recursividade, podemos adivinhar algo, e eventualmente convergirá para os valores reais.

Q-Learning

Agora temos uma estratégia básica – em qualquer estado, execute a ação que acabará gerando a maior recompensa acumulada. Algoritmos como esse são chamados gananciosos, por uma razão óbvia.

Como implementaríamos isso para resolver os desafios da vida real? Uma maneira é desenhar uma tabela para armazenar todas as combinações possíveis de ação e estado e usá-la para salvar os valores Q. Podemos então atualizá-la usando a Equação de Bellman como regra de atualização:

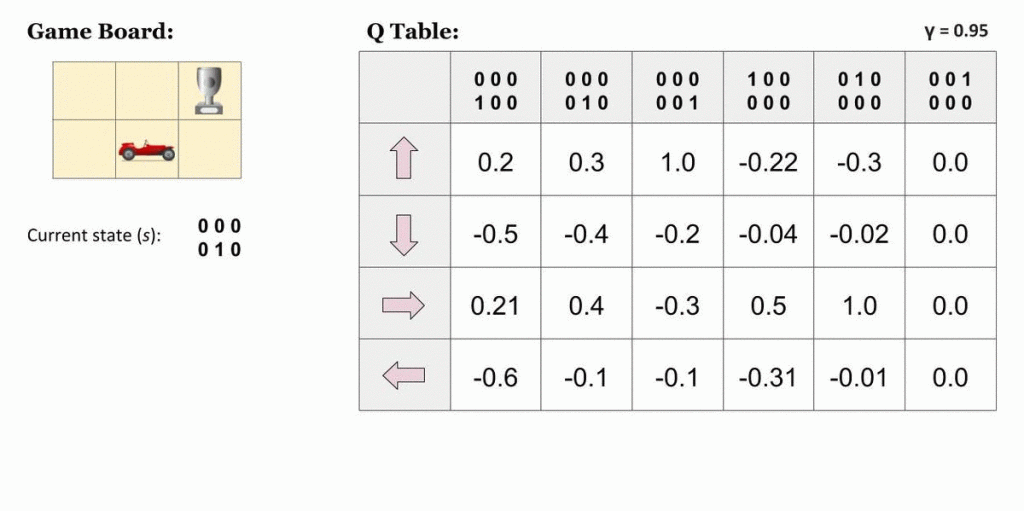
Mas nosso algoritmo ganancioso tem um problema sério: se você continuar selecionando as mesmas melhores ações, nunca tentará algo novo e poderá perder uma abordagem mais gratificante só porque nunca tentou (exatamente como acontece com nós seres humanos).

Para resolver isso, usamos uma abordagem ε-gananciosa: para alguns 0 < ε <1, escolhemos a ação gananciosa (usando nossa tabela) com uma probabilidade p = 1-ε, ou uma ação aleatória com probabilidade p = ε. Assim, damos ao agente a chance de explorar novas oportunidades.

Esse algoritmo é conhecido como Q-Learning e resume o que estudamos nos capítulos anteriores.

Deep Q-Networks

O que acontece quando o número de estados e ações se torna muito grande? Na verdade, isso não é tão raro – mesmo um jogo simples como o Tic Tac Toe tem centenas de estados diferentes (tente calcular isso) e não se esqueça de multiplicarmos esse número por 9, que é o número de ações possíveis. Então, como vamos resolver problemas realmente complexos?

Uma solução possível é a Deep Q-Network! Combinamos Q Learning e Deep Learning, o que gera Deep Q-Networks. A ideia é simples: substituiremos a tabela de valores Q por uma rede neural que tente aproximar os valores Q. É geralmente referido como o aproximador ou a função de aproximação e indicado como Q (s, a; θ), em que θ representa os pesos treináveis da rede.

Agora, só faz sentido usar a Equação de Bellman como a função de custo – mas o que exatamente minimizaremos? Vamos dar uma outra olhada:

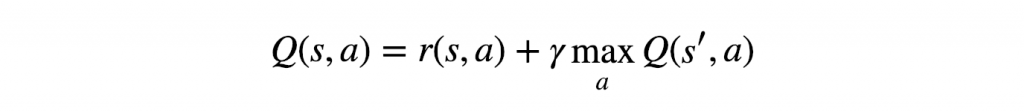
O sinal “=” marca a atribuição, mas existe alguma condição que também satisfaça uma igualdade? Bem, sim – quando o valor Q atingiu seu valor convergente e final. E esse é exatamente o nosso objetivo – para minimizar a diferença entre o lado esquerdo e o lado direito – e bingo!

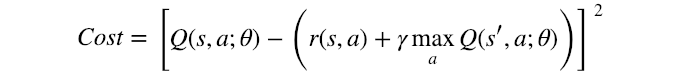
Isso parece familiar? Provavelmente – é a função erro do quadrado médio (função usada em regressão linear, um dos modelos mais básicos em Machine Learning), onde o valor Q atual é a previsão (y) e as recompensas imediatas e futuras são o destino (y’):

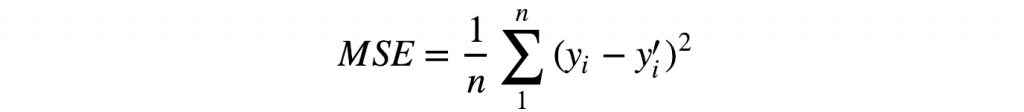
É por isso que Q (s’, a; θ) é geralmente referido como Q-target (a variável target em modelo tradicional de Machine Learning).

Seguindo em frente, precisamos treinar a rede. No Aprendizado por Reforço, o conjunto de treinamento é criado à medida que avançamos; pedimos ao agente para tentar selecionar a melhor ação usando a rede atual – e registramos o estado, a ação, a recompensa e o próximo estado em que ele terminou. Decidimos o tamanho de um lote b e, toda vez que novos registros de b foram gravados, selecionamos b registros aleatoriamente (!!) na memória e treinamos a rede. Os buffers de memória usados geralmente são chamados de Experience Replay. Existem vários tipos de tais memórias – uma muito comum é um buffer de memória cíclico. Isso garante que o agente continue treinando sobre seu novo comportamento, em vez de coisas que podem não ser mais relevantes.

As coisas estão ficando reais, então vamos falar sobre arquitetura: se imitar uma tabela, a rede deve receber como entrada o estado e a ação e deve gerar um valor Q:

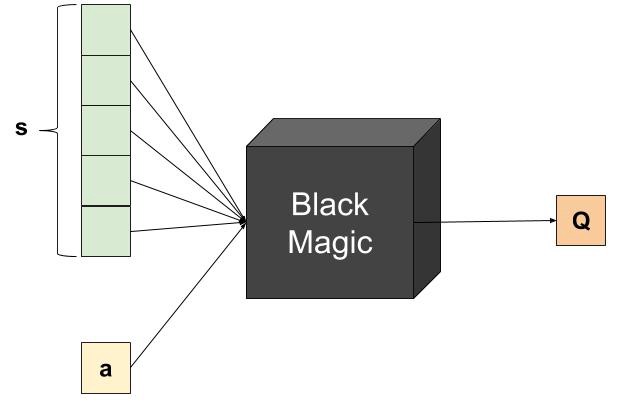
Embora correta, essa arquitetura é muito ineficiente do ponto de vista técnico. Observe que a função de custo requer o valor Q máximo futuro, portanto, precisaremos de várias previsões de rede para um único cálculo de custo. Então, em vez disso, podemos usar a seguinte arquitetura:

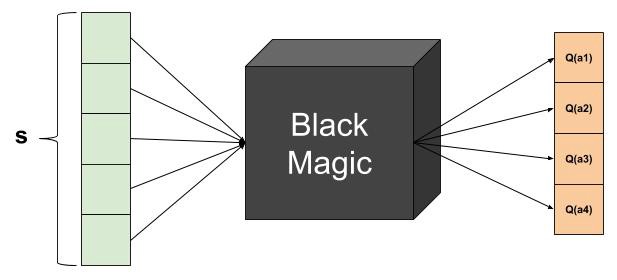
Aqui, fornecemos à rede apenas os estados como entrada e recebemos valores Q para todas as ações possíveis de uma só vez. Muito melhor. E é praticamente isso. Parabéns! Você acabou de aprender sobre um dos modelos mais avançados em Inteligência Artificial. Se vem acompanhando o livro capítulo a capítulo até aqui não deve ter sido tão difícil.

Antes de encerrarmos, aqui está algo extra:

Alguns parágrafos atrás, comparamos a função de custo da Deep Q-Network com o erro quadrado médio. Mas o MSE compara as previsões y aos rótulos verdadeiros y’- e os rótulos verdadeiros são constantes durante todo o procedimento de treinamento. Obviamente, esse não é o caso na Deep Q-Network: y e y’ são previstos pela própria rede e, portanto, podem variar a cada iteração. O impacto é claro.

Por isso usamos a Double Deep Q-Network, que usa rótulos semi-constantes durante o treinamento. Mantemos duas cópias da rede Q, mas apenas uma está sendo atualizada – a outra permanece imóvel. De vez em quando, porém, substituímos a rede constante por uma cópia da Q Network treinada, daí a razão pela qual chamamos de “semi-constante”.

Aqui na Data Science Academy acreditamos que a melhor maneira de entender novos conceitos é praticando e por isso nossos cursos tem um perfil prático, com projetos voltados ao mercado de trabalho e ao que as empresas precisam!

Na próxima traremos um exemplo prático da Deep Q-Network. Até lá.

Referências:

Formação Machine Learning

Customizando Redes Neurais com Funções de Ativação Alternativas

A Beginner’s Guide to Deep Reinforcement Learning

Reinforcement Learning: What is, Algorithms, Applications, Example

What is reinforcement learning? The complete guide

Qrash Course: Reinforcement Learning 101 & Deep Q Networks in 10 Minutes

Reinforcement Learning algorithms — an intuitive overview

Reinforcement learning

Reinforcement Learning, Second Edition

Applications of Reinforcement Learning in Real World