Capítulo 29 – Definindo o Tamanho do Mini-Batch
Quando os dados de treinamento são divididos em pequenos lotes, cada lote recebe o nome de Mini-Batch (ou Mini-Lote). Suponha que os dados de treinamento tenham 32.000 instâncias e que o tamanho de um Mini-Batch esteja definido como 32. Então, haverá 1.000 Mini-Batches. Mas qual deve ser o tamanho do Mini-Batch? Isso é o que veremos neste capítulo: Definindo o Tamanho do Mini-Batch.
Mas porque usamos Mini-Batches? Digamos que você tenha cerca de 1 bilhão de dados de treinamento. Se você decidir usar o conjunto completo de treinamento em cada época, você precisará de muita memória RAM e armazenamento para processar esses dados, sendo bem provável que sua máquina (ou mesmo um cluster de computadores) não tenha memória suficiente. Se você decidir usar um exemplo de treinamento em cada época, de um bilhão de dados, de uma só vez, você está ignorando a filosofia de vetorização e isso tornará o processo de treinamento muito mais lento.
Portanto, usamos um subconjunto de dados de treinamento (chamamos de “Mini-Batch”) de cada vez em cada época. Isso nos permitirá manter os dois objetivos: ajustar dados suficientes na memória do computador e manter a filosofia de vetorização ao mesmo tempo. Uma coisa importante sobre o Mini-Batch é que, é melhor escolher o tamanho do Mini-Batch como múltiplo de 2 e os valores comuns são: 64, 128, 256 e 512. Sinta-se à vontade para usar outros valores e discutiremos mais sobre isso mais a frente aqui mesmo neste capítulo.
Veja um exemplo: digamos que você tenha 1 bilhão de dados de treinamento. Você define seu tamanho de Mini-Batch para, digamos, 512. Portanto, em cada época você tem 512 dados de treinamento para processar. Esta configuração levará aproximadamente: (1.000.000.000 / 512) = 1.953.125 épocas para ser concluída. Portanto, o tamanho do Mini-Batch é a quantidade de dados que você deseja processar em cada época.
Se atualizarmos os parâmetros do modelo após o processamento de todos os dados de treinamento (ou seja, época), levaria muito tempo para obter uma atualização do modelo no treinamento, e os dados de treinamento inteiros provavelmente não caberiam na memória. Se atualizarmos os parâmetros do modelo após o processamento de cada instância (por exemplo, descida de gradiente estocástico), as atualizações do modelo seriam demasiado ruidosas e o processo não seria computacionalmente eficiente.
Portanto, a utilização do Mini-Batch (principalmente na descida do gradiente) é introduzida como um trade-off entre {atualizações rápidas do modelo, eficiência de memória} e {atualizações precisas do modelo, eficiência computacional}. É trabalho do Cientista de Dados ajustar mais esse parâmetro no processo de treinamento.
Mas Como Devemos Definir o Tamanho do Mini-Batch?
Para responder a essa pergunta, vamos primeiro supor que estamos fazendo aprendizado on-line, ou seja, que estamos usando um tamanho de Mini-Batch igual a 1.
A preocupação óbvia sobre o aprendizado online é que o uso de Mini-Lotes que contêm apenas um único exemplo de treinamento causará erros significativos em nossa estimativa do gradiente. A razão é que as estimativas graduais individuais não tem que ser super precisas. Tudo o que precisamos é de uma estimativa precisa o suficiente para que nossa função de custo continue diminuindo. É como se você estivesse tentando chegar ao Pólo Norte, mas tivesse uma bússola informando 10 a 20 graus cada vez que você olhasse para ela. Desde que você pare para checar a bússola com frequência, e a bússola acerte na direção, você acabará chegando ao Pólo Norte.
Com base nesse argumento, parece que devemos usar o aprendizado on-line. De fato, a situação acaba sendo mais complicada do que isso. Em um problema do capítulo anterior, mostramos que é possível usar técnicas de matriz para calcular a atualização de gradiente para todos os exemplos em um Mini-Lote simultaneamente, em vez de fazer um loop sobre eles. Dependendo dos detalhes de seu hardware e da biblioteca de álgebra linear, pode ser um pouco mais rápido calcular a estimativa de gradiente para um Mini-Lote de (por exemplo) tamanho 100, em vez de computar a estimativa de gradiente Mini-Lote fazendo um loop sobre os 100 exemplos de treinamento separadamente. Pode levar (digamos) apenas 50 vezes mais tempo, em vez de 100 vezes mais tempo.
Agora, a princípio, parece que isso não nos ajuda muito. Com nosso Mini-Lote de tamanho 100, a regra de aprendizado para os pesos se parece com:
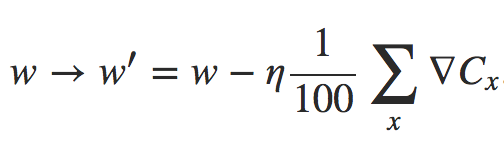
onde a soma é sobre exemplos de treinamento no Mini-Lote. Isso é equivalente a:
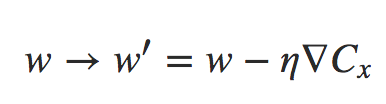
para aprendizagem online. Mesmo que demore 50 vezes mais para fazer a atualização do Mini-Batch, ainda parece ser melhor fazer o aprendizado online, porque estaríamos atualizando com muito mais frequência. Suponha, no entanto, que no caso do Mini-Lote nós aumentemos a taxa de aprendizado por um fator 100, então a regra de atualização se torna:
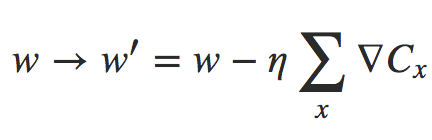
Isso é muito parecido com 100 instâncias separadas de aprendizado online com uma taxa de aprendizado de η. Mas leva apenas 50 vezes mais tempo do que fazer uma única instância de aprendizado online. Naturalmente, não é exatamente o mesmo que 100 instâncias de aprendizado online, já que no Mini-Lote os ∇Cxs são todos avaliados para o mesmo conjunto de pesos, ao contrário do aprendizado cumulativo que ocorre no caso online. Ainda assim, parece claramente possível que o uso do Mini-Lote maior acelere as coisas.
Com esses fatores em mente, escolher o melhor tamanho de Mini-Lote é um trade-off (escolha). Muito pequeno, e você não consegue aproveitar ao máximo os benefícios de boas bibliotecas de matrizes otimizadas para hardware veloz. Demasiado grande e você simplesmente não está atualizando seus pesos com frequência suficiente. O que você precisa é escolher um valor que maximize a velocidade de aprendizado. Felizmente, a escolha do tamanho do Mini-Lote no qual a velocidade é maximizada é relativamente independente dos outros hiperparâmetros (além da arquitetura geral), portanto, você não precisa ter otimizado esses hiperparâmetros para encontrar um bom tamanho Mini-Lote.
O caminho a percorrer é, portanto, usar alguns valores aceitáveis (mas não necessariamente ideais) para os outros hiperparâmetros, e então testar vários tamanhos diferentes de Mini-Lotes, escalando η como fizemos no exemplo acima. Plote a precisão da validação em relação ao tempo (como em tempo real decorrido, não em época!) e escolha o tamanho do Mini-Lote que forneça a melhoria mais rápida no desempenho. Com o tamanho do Mini-Lote escolhido, você pode continuar a otimizar os outros hiperparâmetros. Entendeu agora porque Cientistas de Dados devem ser muito bem remunerados?
Claro, como você, sem dúvida, percebeu, não fizemos essa otimização em nossa rede de exemplo estudada nos capítulos anteriores. De fato, nossa implementação não usa a abordagem mais rápida para atualizações de Mini-Batch. Nós simplesmente usamos um tamanho de Mini-Lote de 10 sem comentários ou explicações em quase todos os exemplos. Por causa disso, poderíamos ter acelerado o aprendizado reduzindo o tamanho do Mini-Lote. Não fizemos isso, em parte porque queríamos ilustrar o uso de Mini-Lotes além do tamanho 1, e em parte porque nossos experimentos preliminares sugeriam que a aceleração seria bastante modesta, uma vez que nossa rede de exemplo é bem simples. Em implementações práticas, no entanto, certamente implementaríamos a abordagem mais rápida para atualizações de Mini-Batch e, em seguida, faríamos um esforço para otimizar o tamanho do Mini-Lote, a fim de maximizar nossa velocidade geral.
Até o próximo capítulo.
Referências:
Matemática e Estatística Aplicada Para Data Science, Machine Learning e IA
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

