Capítulo 55 – Geração de Variáveis Aleatórias – Uma das Bases dos Modelos Generativos em GANs (Generative Adversarial Networks)
Neste capítulo discutiremos o processo de geração de variáveis aleatórias a partir de uma determinada distribuição, tema importante para compreender o funcionamento dos modelos generativos das GANs e nos próximos capítulos veremos os detalhes de funcionamento dos modelos generativos e os detalhes matemáticos das GANs. Estamos considerando que você leu o capítulo anterior.
Variáveis aleatórias uniformes podem ser geradas pseudo-aleatoriamente
Vamos começar discutindo o processo de geração de variáveis aleatórias. Veremos alguns métodos existentes e, mais especificamente, o método de transformação inversa que permite gerar variáveis aleatórias complexas a partir de variáveis aleatórias uniformes simples. Embora tudo isso possa parecer um pouco distante do nosso assunto, GANs, veremos no próximo capítulo o vínculo profundo que existe com os modelos generativos. Se o conceito de Estatística for algo que você esteja vendo pela primeira vez, a DSA oferece cursos completos de Estatística e Matemática na Formação Análise Estatística.
Uma variável aleatória é uma variável quantitativa, cujo resultado (valor) depende de fatores aleatórios. Um exemplo de uma variável aleatória é o resultado do lançamento de um dado que pode resultar em qualquer número entre 1 e 6. Embora possamos conhecer os seus possíveis resultados, o resultado em si depende de fatores de sorte (álea). Uma variável aleatória pode ser uma medição de um parâmetro que pode gerar valores diferentes. O conceito de variável aleatória é essencial em Estatística e em outros métodos quantitativos para a representação de fenômenos incertos. Este conceito é estudado em detalhes no curso Análise Estatística Para Data Science com Linguagem R.
As variáveis aleatórias podem ser classificadas em variáveis aleatórias discretas, contínuas e mistas.
Os computadores são fundamentalmente determinísticos. Portanto, é teoricamente impossível gerar números realmente aleatórios (a pergunta “o que realmente é aleatoriedade?” é algo difícil de responder). No entanto, é possível definir algoritmos que geram sequências de números cujas propriedades estão muito próximas das propriedades das sequências teóricas de números aleatórios. Em particular, um computador é capaz, usando um gerador de números pseudo-aleatórios, de gerar uma sequência de números que segue aproximadamente uma distribuição aleatória uniforme entre 0 e 1. O caso uniforme é muito simples, no qual variáveis aleatórias mais complexas podem ser construídas.
Variáveis aleatórias expressas como resultado de uma operação ou processo
Existem diferentes técnicas que visam gerar variáveis aleatórias mais complexas. Entre elas, podemos encontrar, por exemplo, método de transformação inversa, amostragem por rejeição, algoritmo Metropolis-Hastings entre outros. Todos esses métodos se baseiam em diferentes truques matemáticos que consistem principalmente em representar a variável aleatória que queremos gerar como resultado de uma operação (sobre variáveis aleatórias mais simples) ou de um processo.
A amostragem por rejeição expressa a variável aleatória como resultado de um processo que consiste em amostrar não da distribuição complexa, mas de uma distribuição simples bem conhecida e para aceitar ou rejeitar o valor amostrado, dependendo de alguma condição. Repetindo esse processo até que o valor amostrado seja aceito, podemos mostrar que, com a condição correta de aceitação, o valor que será efetivamente amostrado seguirá a distribuição correta.
No algoritmo Metropolis-Hastings, a ideia é encontrar uma Cadeia de Markov (MC – Markov Chain) de modo que a distribuição estacionária dessa MC corresponda à distribuição da qual gostaríamos de amostrar nossa variável aleatória. Uma vez encontrada essa MC, podemos simular uma trajetória longa o suficiente sobre ela para considerar que atingimos um estado estacionário e, em seguida, o último valor que obtemos dessa maneira pode ser considerado como extraído da distribuição de interesse.
Não iremos mais adiante nos detalhes da amostragem por rejeição e do Metropolis-Hastings, porque esses métodos não são os que nos levarão à noção por trás das GANs. No entanto, vamos nos concentrar um pouco mais no método de transformação inversa.
O método de transformação inversa
A ideia do método de transformação inversa é simplesmente representar nossa “complexa” variável aleatória como resultado de uma função aplicada a um variável aleatória uniforme, que nós sabemos como gerar.
Consideramos abaixo um exemplo unidimensional. Seja X uma variável aleatória complexa da qual queremos amostrar e U seja uma variável aleatória uniforme sobre [0,1] que sabemos como amostrar. Lembramos que uma variável aleatória é totalmente definida por sua Função de Distribuição Cumulativa (CDF). O CDF de uma variável aleatória é uma função do domínio de definição da variável aleatória até o intervalo [0,1] e definido, em uma dimensão, de modo que:
![]()
No caso particular de nossa variável aleatória uniforme U, temos:
![]()
Por uma questão de simplicidade, vamos supor aqui que a função CDF_X é inversível e seu inverso é indicado por:
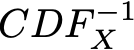
(o método pode ser facilmente estendido ao caso não inversível usando o inverso generalizado da função, mas não é realmente o ponto principal em que queremos focar aqui). Então, se definirmos:
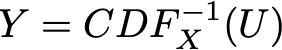
temos:
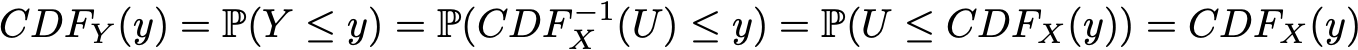
Como podemos ver, Y e X têm o mesmo CDF e depois definem a mesma variável aleatória. Assim, definindo Y como acima (em função de uma variável aleatória uniforme), conseguimos definir uma variável aleatória com a distribuição alvo.
Para resumir, o método de transformação inversa é uma maneira de gerar uma variável aleatória que segue uma determinada distribuição, fazendo uma variável aleatória uniforme passar por uma “função de transformação” bem projetada (CDF inverso). Essa noção de “método de transformação inversa” pode, de fato, ser estendida à noção de “método de transformação” que consiste, de maneira mais geral, em gerar variáveis aleatórias em função de algumas variáveis aleatórias mais simples (não necessariamente uniformes e, em seguida, a função de transformação é não mais o CDF inverso). Conceitualmente, o objetivo da “função de transformação” é deformar / remodelar a distribuição de probabilidade inicial: a função de transformação começa de onde a distribuição inicial é muito alta em comparação com a distribuição de destino e a coloca onde é muito baixa. Foi exatamente isso que pensou o criador do modelo GAN e muitos consideram o conceito como uma espécie de “hack” na teoria estatística, o que gerou o modelo GAN.
Observe a ilustração do método de transformação inversa abaixo. Em azul: a distribuição uniforme em [0,1]. Em laranja: a distribuição gaussiana (normal) padrão. Em cinza: o mapeamento da distribuição uniforme para a gaussiana (CDF inverso).
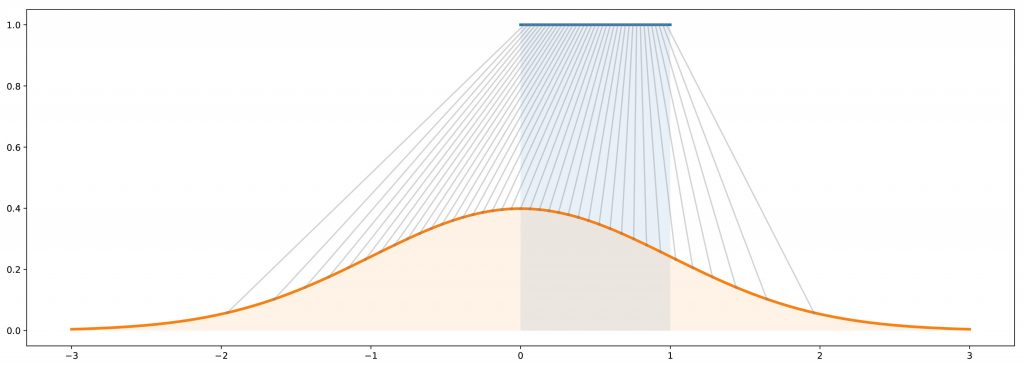
Compreendeu o conceito? Isso é o que está por trás dos modelos generativos nas GANs, que veremos no próximo capítulo!
Referências:
Análise Estatística Para Data Science com Linguagem Python
Customizando Redes Neurais com Funções de Ativação Alternativas
A Beginner’s Guide to Generative Adversarial Networks (GANs)
A Leap into the Future: Generative Adversarial Networks
Understanding Generative Adversarial Networks (GANs)
How A.I. Is Creating Building Blocks to Reshape Music and Art
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
Recurrent neural network based language model
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Gradient Descent For Machine Learning
Pattern Recognition and Machine Learning

