Capítulo 53 – Matemática na GRU, Dissipação e Clipping do Gradiente

A capacidade da rede GRU de manter dependências ou memória de longo prazo decorre dos cálculos na célula na GRU para produzir o estado oculto. As LSTMs têm dois estados diferentes passados entre as células – o estado da célula e o estado oculto, que carregam a memória de longo e curto prazo, respectivamente – as GRUs têm apenas um estado oculto transferido entre as etapas do tempo. Esse estado oculto é capaz de manter as dependências de longo e curto prazo ao mesmo tempo, devido aos mecanismos de restrição (portões) e cálculos pelos quais o estado oculto e os dados de entrada passam.

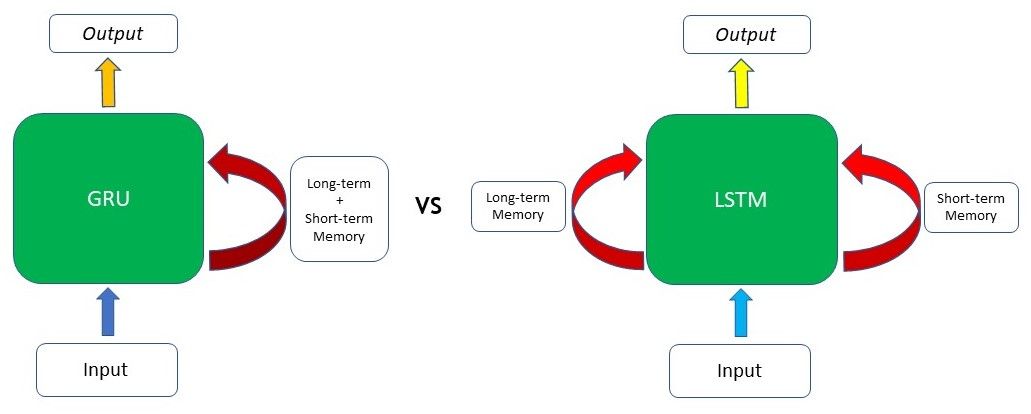
A célula GRU contém apenas dois portões: o portão de atualização e o portão de redefinição. Assim como os portões das LSTMs, os portões na GRU são treinados para filtrar seletivamente qualquer informação irrelevante, mantendo o que é útil. Esses portões são essencialmente vetores contendo valores entre 0 e 1 que serão multiplicados com os dados de entrada e/ou estado oculto. Um valor 0 nos vetores indica que os dados correspondentes no estado de entrada ou oculto não são importantes e, portanto, retornarão como zero. Por outro lado, um valor 1 no vetor significa que os dados correspondentes são importantes e serão usados.

Usaremos os termos gate e vetor de forma intercambiável para o restante deste capítulo, pois eles se referem à mesma coisa.

A estrutura de uma unidade GRU é mostrada abaixo.

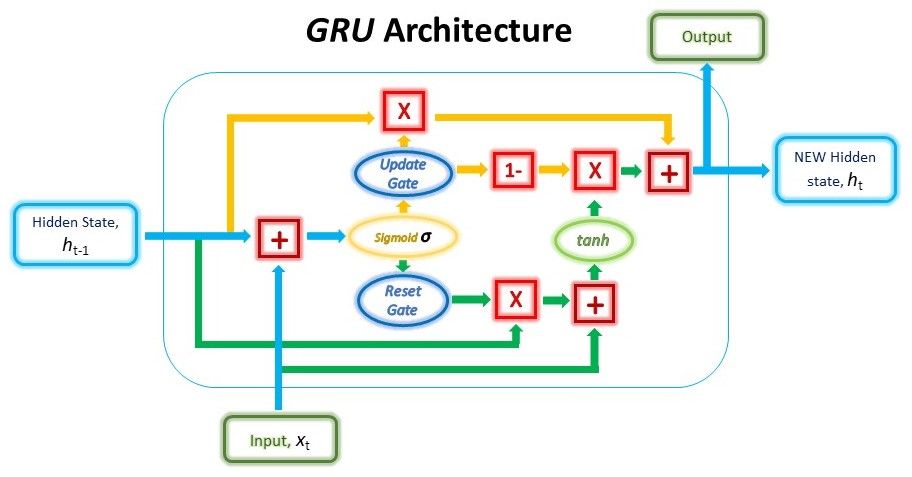
Embora a estrutura possa parecer bastante complicada devido ao grande número de conexões, o mecanismo por trás dela pode ser dividido em três etapas principais.

Reset Gate

Na primeira etapa, criamos o portão de redefinição (reset gate). Essa porta é derivada e calculada usando o estado oculto da etapa anterior e os dados de entrada na etapa atual.

Matematicamente, isso é conseguido multiplicando o estado oculto anterior e a entrada atual com seus respectivos pesos e somando-os antes de passar a soma através de uma função sigmóide. A função sigmoide transformará os valores entre 0 e 1, permitindo que o portão filtre entre as informações menos importantes e mais importantes nas etapas subsequentes. A fórmula matemática é representada abaixo:

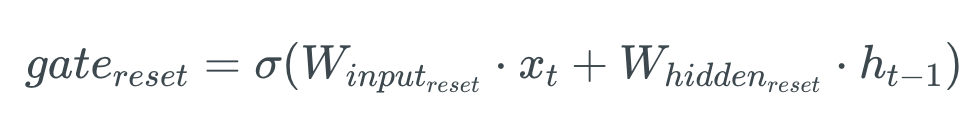
Quando toda a rede é treinada através de backpropagation, os pesos na equação serão atualizados de forma que o vetor aprenda a reter apenas os recursos úteis.

O estado oculto anterior será primeiro multiplicado por um peso treinável e passará por uma multiplicação por elementos (produto Hadamard) com o vetor de redefinição. Esta operação decidirá quais informações serão mantidas nas etapas anteriores, juntamente com as novas entradas. Ao mesmo tempo, a entrada atual também será multiplicada por um peso treinável antes de ser somada com o produto do vetor de redefinição e do estado oculto anterior acima. Por fim, uma função tanh de ativação não linear será aplicada ao resultado final para obter r na equação abaixo.

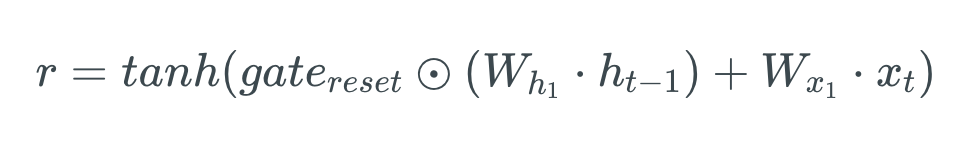
Update Gate

Em seguida, temos o portão de atualização (update gate). Assim como o reset gate, o update gate é calculado usando o estado oculto anterior e os dados de entrada atuais.

Os vetores Update e Reset gate são criados usando a mesma fórmula, mas os pesos multiplicados pela entrada e pelo estado oculto são exclusivos para cada portão, o que significa que os vetores finais para cada portão são diferentes. Isso permite que os portões sirvam a seus propósitos específicos.

O vetor Update será submetido a multiplicação por elementos com o estado oculto anterior para obter u em nossa equação abaixo, que será usada para calcular nossa saída final posteriormente.

O vetor Update também será usado em outra operação posteriormente ao obter nossa saída final. O objetivo do update gate aqui é ajudar o modelo a determinar quanto das informações passadas armazenadas no estado oculto anterior precisam ser retidas para o futuro.

Combinando as Saídas

Na última etapa, reutilizaremos o portal Update e obteremos o estado oculto atualizado.

Desta vez, pegaremos a versão inversa em elementos do mesmo vetor Update (1 – Update gate) e faremos uma multiplicação em elementos com a nossa saída do reset gate, r. O objetivo desta operação é o gate Update determinar qual parte das novas informações deve ser armazenada no estado oculto.

Por fim, o resultado das operações acima será resumido com a nossa saída do portão Update na etapa anterior, u. Isso nos dará nosso novo e atualizado estado oculto.

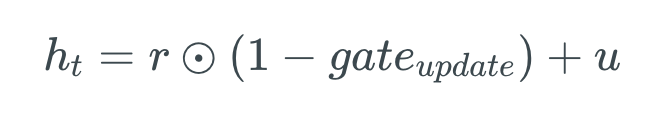
Podemos usar esse novo estado oculto como nossa saída para esse intervalo de tempo, passando-o por uma camada de ativação linear.

Solução do Problema de Dissipação/Explosão do Gradiente

Vimos os portões em ação. Sabemos como eles transformam nossos dados. Agora, vamos revisar seu papel geral no gerenciamento da memória da rede e falar sobre como eles resolvem o problema de dissipação/explosão do gradiente.

Como vimos nos mecanismos acima, o Reset Gate é responsável por decidir quais partes do estado oculto anterior devem ser combinadas com a entrada atual para propor um novo estado oculto.

E o Update Gate é responsável por determinar quanto do estado oculto anterior deve ser retido e qual parte do novo estado oculto proposto (derivado do Reset Gate) deve ser adicionado ao estado oculto final. Quando o Update Gate é multiplicado pela primeira vez com o estado oculto anterior, a rede escolhe quais partes do estado oculto anterior ele manterá em sua memória enquanto descarta o restante. Posteriormente, ele corrige as partes ausentes das informações quando usa o inverso do gate Update para filtrar o novo estado oculto proposto a partir do Reset Gate.

Isso permite que a rede retenha dependências de longo prazo. O Update Gate pode optar por manter a maioria das memórias anteriores no estado oculto se os valores do vetor Update estiverem próximos de 1 sem recalcular ou alterar todo o estado oculto.

O problema de dissipação/explosão do gradiente ocorre durante a propagação de retorno (backpropagation) ao treinar a RNN, especialmente se a RNN estiver processando longas sequências ou tiver várias camadas. O erro do gradiente calculado durante o treinamento é usado para atualizar o peso da rede na direção certa e na magnitude certa. No entanto, esse gradiente é calculado com a regra da cadeia (chain rule), começando no final da rede. Portanto, durante o backpropagation, os gradientes sofrerão continuamente multiplicações de matrizes e encolherão ou explodirão exponencialmente por sequências longas. Ter um gradiente muito pequeno significa que o modelo não atualiza seus pesos de maneira eficaz, enquanto gradientes extremamente grandes fazem com que o modelo seja instável.

Os portões nas LSTM e GRUs ajudam a resolver esse problema devido ao componente aditivo dos portões de atualização. Enquanto as RNNs tradicionais sempre substituem todo o conteúdo do estado oculto a cada etapa, as LSTMs e GRUs mantêm a maior parte do estado oculto existente enquanto adicionam novo conteúdo sobre ele. Isso permite que os erros dos gradientes sejam propagados de volta sem desaparecer ou explodir muito rapidamente devido às operações de adição.

Clipping (Recorte) do Gradiente

Embora LSTMs e GRUs sejam as correções mais usadas para o problema acima, outra solução para o problema de explosão de gradientes é o clipping do gradiente.

O clipping do gradiente é mais comum em redes neurais recorrentes. Quando os gradientes estão sendo propagados no tempo, eles podem desaparecer porque são continuamente multiplicados por números menores que um. Isso é chamado de problema de dissipação do gradiente, podendo ser resolvido por LSTMs e GRUs e, se você estiver usando uma rede profunda feed-forward, isso é resolvido por conexões residuais. Por outro lado, você também pode ter explosão dos gradientes. É quando eles se tornam exponencialmente grandes por serem multiplicados por números maiores que 1. O clipping do gradiente cortará os gradientes entre dois números para impedir que eles fiquem muito grandes.

O clipping define um valor limite definido nos gradientes, o que significa que, mesmo se um gradiente aumentar além do valor predefinido durante o treinamento, seu valor ainda será limitado ao limite definido. Dessa forma, a direção do gradiente permanece inalterada e apenas a magnitude do gradiente é alterada.

Até o próximo capítulo!

Referências:

Formação Engenheiro de Inteligência Artificial

Customizando Redes Neurais com Funções de Ativação Alternativas

Understanding GRU Networks

Illustrated Guide to LSTM’s and GRU’s: A step by step explanation

Gated Recurrent Unit (GRU)

A Recursive Recurrent Neural Network for Statistical Machine Translation

Sequence to Sequence Learning with Neural Networks

Recurrent Neural Networks Cheatsheet

On the difficulty of training recurrent neural networks

A Beginner’s Guide to LSTMs and Recurrent Neural Networks