Capítulo 56 – Modelos Generativos – O Diferencial das GANs (Generative Adversarial Networks)

Neste capítulo discutiremos o funcionamento dos modelos generativos, o principal diferencial nas GANs (Generative Adversarial Networks). Estamos considerando que você leu o capítulo anterior.

Suponha que estamos interessados em gerar imagens quadradas em preto e branco de cães com um tamanho de n por n pixels. Podemos remodelar cada dado como um vetor dimensional N = n x n (empilhando colunas umas sobre as outras), de modo que uma imagem de cachorro possa ser representada por um vetor (quem sabe conseguimos criar um modelo capaz de diferenciar um Muffin de um Chihuahua).

No entanto, isso não significa que todos os vetores representem um cão que foi moldado de volta a um quadrado! Portanto, podemos dizer que os vetores dimensionais N que efetivamente geram algo que se parece com um cachorro são distribuídos de acordo com uma distribuição de probabilidade muito específica em todo o espaço vetorial dimensional N (alguns pontos desse espaço provavelmente representam cães, enquanto é improvável para alguns outros). No mesmo espírito, existe, nesse espaço vetorial dimensional N, distribuições de probabilidade para imagens de gatos, pássaros e assim por diante.

Então, o problema de gerar uma nova imagem do cão é equivalente ao problema de gerar um novo vetor após a “distribuição de probabilidade do cão” no espaço vetorial dimensional N. De fato, estamos enfrentando um problema de gerar uma variável aleatória com relação a uma distribuição de probabilidade específica (lembra do que discutimos no capítulo anterior?).

Neste ponto, podemos mencionar duas coisas importantes. Primeiro, a “distribuição de probabilidade canina” que mencionamos é uma distribuição muito complexa em um espaço muito grande. Segundo, mesmo se pudermos assumir a existência de tal distribuição subjacente (na verdade existem imagens que se parecem com cachorro e outras que não), obviamente não sabemos como expressar explicitamente essa distribuição. Os dois pontos anteriores dificultam bastante o processo de geração de variáveis aleatórias a partir dessa distribuição. Vamos tentar resolver esses dois problemas a seguir.

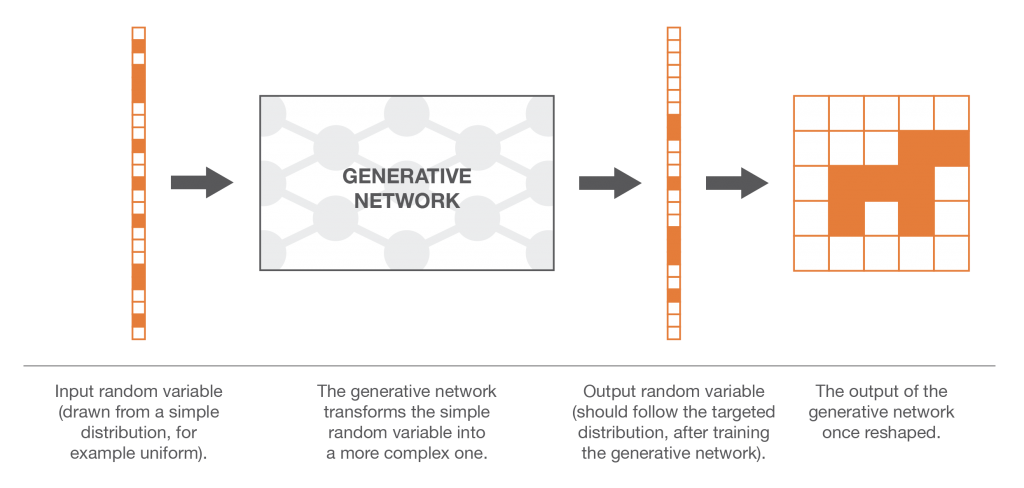
Nosso primeiro problema ao tentar gerar nossa nova imagem de cachorro é que a “distribuição de probabilidade do cachorro” no espaço vetorial dimensional N é muito complexa e não sabemos como gerar diretamente variáveis aleatórias complexas. No entanto, como sabemos muito bem como gerar N variáveis aleatórias uniformes não correlacionadas, poderíamos fazer uso do método de transformação. Para fazer isso, precisamos expressar nossa variável aleatória N dimensional como resultado de uma função muito complexa aplicada a uma variável aleatória N dimensional simples!

Aqui, podemos enfatizar o fato de que encontrar a função de transformação não é tão simples quanto tomar a inversa de forma fechada da Função de Distribuição Cumulativa (que obviamente não sabemos) como fizemos ao descrever o método de transformação inversa no capítulo anterior. A função de transformação não pode ser expressa explicitamente e, então, precisamos aprender com os dados (essa é uma das razões pelas quais treinamos um modelo de Machine Learning e esse conceito é estudado em detalhes aqui).

Em seguida, a ideia é modelar a função de transformação por uma rede neural que tome como entrada uma variável aleatória uniforme N dimensional simples e que retorne como saída outra variável aleatória N dimensional que deve seguir, após o treinamento, a “distribuição de probabilidade canina” correta . Depois que a arquitetura da rede foi projetada, ainda precisamos treiná-la. Nas próximas duas seções, discutiremos duas maneiras de treinar essas redes generativas, incluindo a ideia de treinamento antagônico por trás das GANs!

Redes de Correspondência Generativa (Generative Matching Networks)

Obs: a denominação de “redes de correspondência generativa” não é padrão. No entanto, podemos encontrar na literatura, por exemplo, “Redes de correspondência de momentos generativos” ou também “Redes de correspondência de recursos generativos”. Só queremos aqui usar uma denominação um pouco mais geral para o que descrevemos abaixo.

Treinando Modelos Generativos

Até agora, mostramos que nosso problema de gerar uma nova imagem de cachorro pode ser reformulado em um problema de gerar um vetor aleatório no espaço vetorial dimensional N que segue a “distribuição de probabilidade canina” e sugerimos o uso de um método de transformação , com uma rede neural para modelar a função de transformação.

Agora, ainda precisamos treinar (otimizar) a rede para expressar a função de transformação correta. Para isso, podemos sugerir dois métodos diferentes de treinamento: um direto e um indireto. O método de treinamento direto consiste em comparar as distribuições de probabilidade verdadeira e gerada e retropropagar a diferença (o erro) através da rede. Essa é a ideia que governa as redes de correspondência generativa (GMNs – Generative Matching Networks)).

Para o método de treinamento indireto, não comparamos diretamente as distribuições verdadeiras e geradas. Em vez disso, treinamos a rede generativa, fazendo com que essas duas distribuições passem por um ajuste escolhido de forma que o processo de otimização da rede generativa em relação à tarefa ajustada imponha que a distribuição gerada esteja próxima da verdadeira distribuição. Essa última ideia é a que está por trás das Redes Adversárias Generativas (GANs) que apresentaremos na próxima seção. Mas, por enquanto, vamos começar com o método direto e as GMNs.

Comparando duas distribuições de probabilidade com base em amostras

Como mencionado, a ideia das GMNs é treinar a rede generativa comparando diretamente a distribuição gerada com a verdadeira. No entanto, não sabemos como expressar explicitamente a verdadeira “distribuição de probabilidade de cães” e também podemos dizer que a distribuição gerada é complexa demais para ser expressa explicitamente. Portanto, comparações baseadas em expressões explícitas não são possíveis. Logo, se tivermos uma maneira de comparar distribuições de probabilidade com base em amostras, podemos usá-la para treinar a rede. De fato, temos uma amostra de dados verdadeiros e podemos, a cada iteração do processo de treinamento, produzir uma amostra de dados gerados.

Embora, em teoria, qualquer distância (ou medida de similaridade) capaz de comparar efetivamente duas distribuições baseadas em amostras possa ser usada, podemos mencionar, em particular, a abordagem da Discrepância Média Máxima (MMD). O MMD define uma distância entre duas distribuições de probabilidade que podem ser calculadas (estimadas) com base em amostras dessas distribuições. Embora não esteja totalmente fora do escopo deste capítulo, decidimos não gastar muito mais tempo descrevendo o MMD. No entanto, caso você queira mais detalhes sobre isso, recomendamos esses 3 papers abaixo:

Learning features to compare distributions

A Kernel Method for the Two-Sample-Problem

A Kernel Two-Sample Test

Retropropagação do erro de correspondência de distribuição

Assim, uma vez que definimos uma maneira de comparar duas distribuições com base em amostras, podemos definir o processo de treinamento da rede generativa em GMNs. Dada uma variável aleatória com distribuição de probabilidade uniforme como entrada, queremos que a distribuição de probabilidade da saída gerada seja a “distribuição de probabilidade do cão”. A ideia das GMNs é otimizar a rede repetindo as seguintes etapas:

Gerar algumas entradas uniformes.
Fazer essas entradas passarem pela rede e coletar as saídas geradas.
Comparar a verdadeira “distribuição de probabilidade de cães” e a gerada com base nas amostras disponíveis (por exemplo, calculando a distância MMD entre a amostra de imagens reais de cães e a amostra de imagens geradas).
Usar retropropagação para fazer uma etapa de descida de gradiente para diminuir a distância (por exemplo, MMD) entre distribuições verdadeiras e geradas.

Conforme descrito acima, ao seguir estas etapas, aplicamos uma descida do gradiente na rede com uma função de perda que é a distância entre as distribuições verdadeiras e as distribuições geradas na iteração atual.

O método de treinamento “indireto”

A abordagem “direta” apresentada acima compara diretamente a distribuição gerada com a verdadeira ao treinar a rede generativa. A brilhante ideia que governa as GANs consiste em substituir essa comparação direta por uma indireta que assume a forma de uma tarefa ajustada sobre essas duas distribuições.

O treinamento da rede generativa é então realizado com relação a essa tarefa, de modo que força a distribuição gerada a se aproximar cada vez mais da distribuição verdadeira.

A tarefa ajustada das GANs é uma tarefa de discriminação entre amostras verdadeiras e geradas. Ou poderíamos dizer uma tarefa de “não discriminação”, pois queremos que a discriminação falhe o máximo possível. Portanto, em uma arquitetura GAN, temos um discriminador, que coleta amostras de dados verdadeiros e gerados e tenta classificá-los da melhor maneira possível, e um gerador treinado para enganar o discriminador o máximo possível. Vamos ver em um exemplo simples porque as abordagens diretas e indiretas que mencionamos devem, em teoria, levar ao mesmo gerador ideal.

O caso ideal: gerador e discriminador perfeitos

Para entender melhor por que treinar um gerador para enganar um discriminador levará ao mesmo resultado que treinar diretamente o gerador para corresponder à distribuição de destino, vamos dar um exemplo unidimensional simples. Esquecemos, por enquanto, como o gerador e o discriminador são representados e os consideramos como noções abstratas (que serão especificadas na próxima subseção). Além disso, ambos são supostos “perfeitos” (com capacidades infinitas) no sentido de que não são limitados por nenhum tipo de modelo (parametrizado).

Suponha que tenhamos uma distribuição verdadeira, por exemplo, um gaussiano unidimensional e que desejemos um gerador que faça amostras dessa distribuição de probabilidade. O que chamamos de método de treinamento “direto” consistiria em ajustar iterativamente o gerador (iterações de descida de gradiente) para corrigir a diferença / erro medido entre distribuições verdadeiras e geradas. Por fim, supondo que o processo de otimização seja perfeito, devemos terminar com a distribuição gerada que corresponda exatamente à verdadeira distribuição.

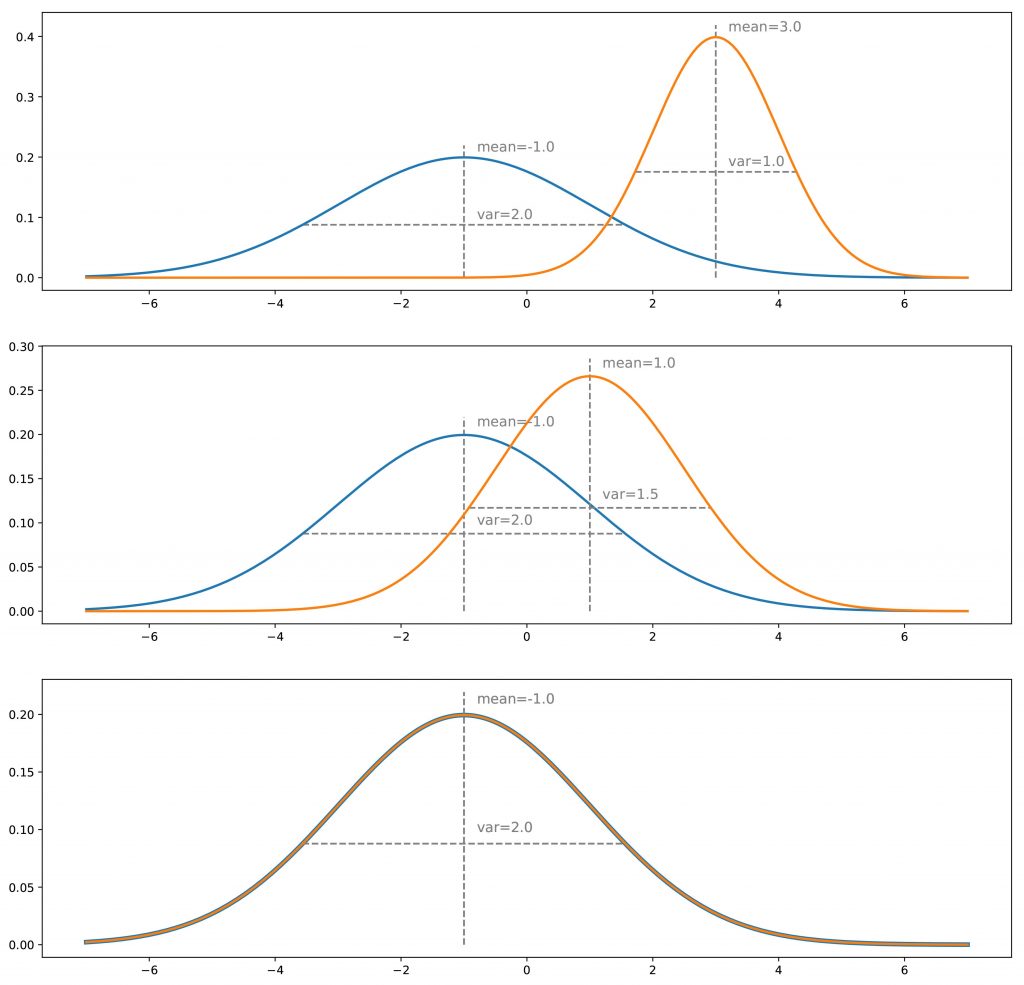
Para a abordagem “indireta”, devemos considerar também um discriminador. Presumimos por enquanto que esse discriminador é um tipo de oráculo que sabe exatamente quais são as distribuições verdadeira e gerada e que é capaz, com base nessas informações, de prever uma classe (“verdadeira” ou “gerada”) para qualquer ponto. Se as duas distribuições estiverem distantes, o discriminador será capaz de classificar facilmente e com um alto nível de confiança a maioria dos pontos que apresentamos. Se queremos enganar o discriminador, precisamos aproximar a distribuição gerada da verdadeira. O discriminador terá mais dificuldade em prever a classe quando as duas distribuições serão iguais em todos os pontos: nesse caso, para cada ponto, haverá chances iguais de ser “verdadeiro” ou “gerado” e, em seguida, o discriminador poderá ” fazer melhor do que ser verdadeiro em um caso em dois em média.

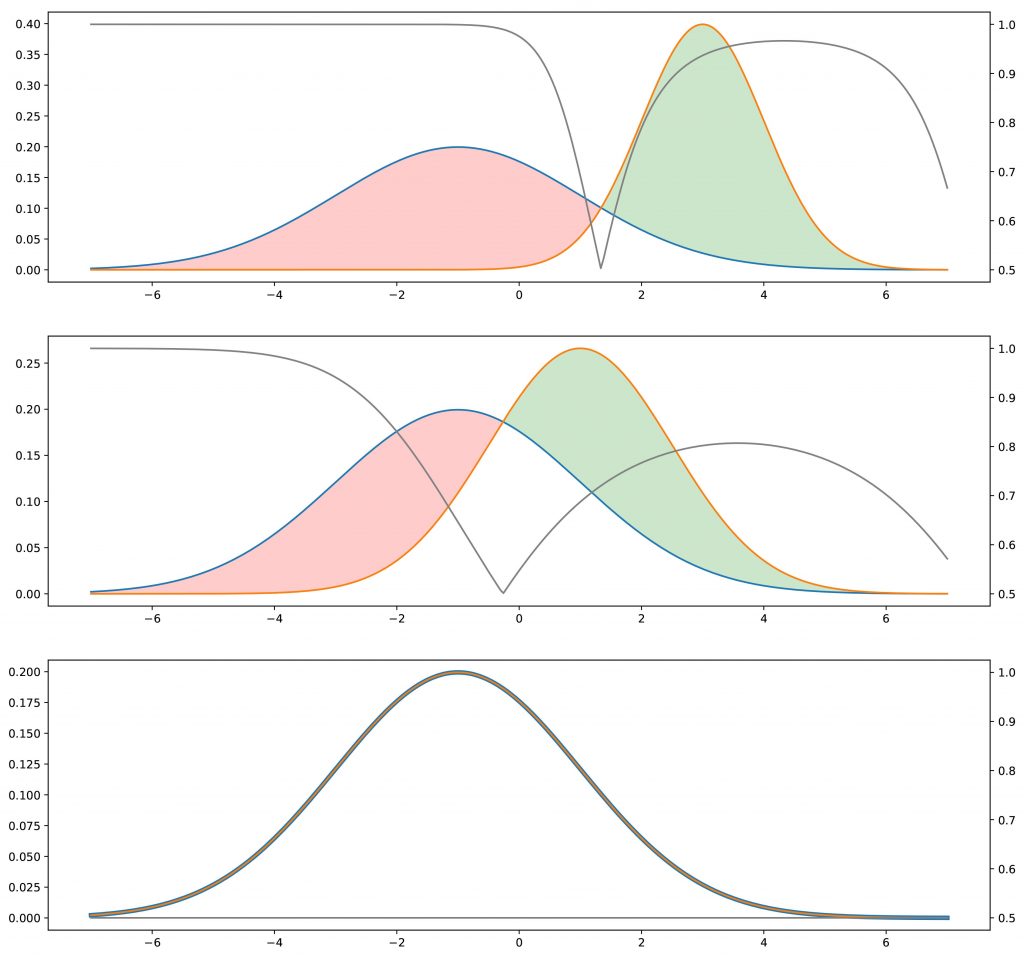
Nesse ponto, parece legítimo se perguntar se esse método indireto é realmente uma boa ideia. De fato, parece ser mais complicado (temos que otimizar o gerador com base em uma tarefa ajustada, em vez de diretamente nas distribuições) e requer um discriminador que consideramos aqui como um determinado oráculo, mas que, na realidade, não é conhecido. Nem perfeito. Para o primeiro ponto, a dificuldade de comparar diretamente duas distribuições de probabilidade com base em amostras contrabalança a aparente maior complexidade do método indireto. Para o segundo ponto, é óbvio que o discriminador não é conhecido. No entanto, pode ser aprendido!

A aproximação: redes neurais adversárias

Vamos agora descrever a forma específica que assume o gerador e o discriminador na arquitetura das GANs. O gerador é uma rede neural que modela uma função de transformação. Ele assume como entrada uma variável aleatória simples e deve retornar, uma vez treinada, uma variável aleatória que segue a distribuição de destino. Como é muito complicado e desconhecido, decidimos modelar o discriminador com outra rede neural. Essa rede neural modela uma função discriminativa. Ele toma como entrada um ponto (no nosso exemplo de cachorro, um vetor dimensional N) e retorna como saída a probabilidade desse ponto ser “verdadeiro”.

Observe que o fato de impormos agora um modelo parametrizado para expressar tanto o gerador quanto o discriminador (em vez das versões idealizadas na subseção anterior) não tem, na prática, um grande impacto no argumento / intuição teórica acima: apenas trabalhamos em alguns espaços parametrizados em vez de espaços completos ideais e, portanto, os pontos ideais que devemos alcançar no caso ideal podem ser vistos como “arredondados” pela capacidade de precisão dos modelos parametrizados.

Uma vez definidas, as duas redes podem ser treinadas em conjunto (ao mesmo tempo) com objetivos opostos:

O objetivo do gerador é enganar o discriminador; portanto, a rede neural generativa é treinada para maximizar o erro de classificação final (entre dados verdadeiros e gerados).
O objetivo do discriminador é detectar dados falsos gerados, para que a rede neural discriminativa seja treinada para minimizar o erro de classificação final.

Portanto, a cada iteração do processo de treinamento, os pesos da rede generativa são atualizados para aumentar o erro de classificação (subida do gradiente de erro sobre os parâmetros do gerador), enquanto os pesos da rede discriminativa são atualizados para diminuir esse erro (descida do gradiente de erro sobre os parâmetros do discriminador).

Esses objetivos opostos e a noção implícita de treinamento antagônico das duas redes explicam o nome de “redes adversárias”: ambas as redes tentam se derrotar e, ao fazê-lo, estão cada vez melhor. A competição entre elas faz com que essas duas redes “progridam” com relação a seus respectivos objetivos. Do ponto de vista da teoria dos jogos, podemos pensar nessa configuração como um jogo minimax para dois jogadores, em que o estado de equilíbrio corresponde à situação em que o gerador produz dados a partir da distribuição exata e onde o discriminador prediz “verdadeiro” ou “gerado” com probabilidade 1/2 para qualquer ponto que receber.

Os modelos GAN estão entre os mais avançados em Deep Learning e a ideia por trás da sua concepção é simples e brilhante.

Agora sim, estamos prontos para compreender a Matemática que faz tudo isso acontecer!

Está gostando do Deep Learning Book? Então ajude a continuarmos esse trabalho e compartilhe o Deep Learning Book entre seus amigos e rede de contatos.

Até o próximo capítulo!

Referências:

Formação Engenheiro de Inteligência Artificial

Customizando Redes Neurais com Funções de Ativação Alternativas

A Beginner’s Guide to Generative Adversarial Networks (GANs)

A Leap into the Future: Generative Adversarial Networks

Understanding Generative Adversarial Networks (GANs)

How A.I. Is Creating Building Blocks to Reshape Music and Art

Train longer, generalize better: closing the generalization gap in large batch training of neural networks

Practical Recommendations for Gradient-Based Training of Deep Architectures

Gradient-Based Learning Applied to Document Recognition

Neural Networks & The Backpropagation Algorithm, Explained