Capítulo 7 – O Perceptron – Parte 2
O Perceptron é um modelo matemático de um neurônio biológico. Enquanto nos neurônios reais o dendrito recebe sinais elétricos dos axônios de outros neurônios, no Perceptron estes sinais elétricos são representados como valores numéricos. Nas sinapses entre dendritos e axônio, os sinais elétricos são modulados em várias quantidades. Isso também é modelado no Perceptron multiplicando cada valor de entrada por um valor chamado peso. Um neurônio real dispara um sinal de saída somente quando a força total dos sinais de entrada excede um certo limiar. Nós modelamos esse fenômeno em um Perceptron calculando a soma ponderada das entradas para representar a força total dos sinais de entrada e aplicando uma função de ativação na soma para determinar sua saída. Tal como nas redes neurais biológicas, esta saída é alimentada em outros Perceptrons. Estudamos tudo isso no capítulo anterior. Agora vamos continuar nossa discussão sobre o Perceptron compreendendo mais alguns conceitos, que serão fundamentais mais a frente quando estudarmos as arquiteturas avançadas de Deep Learning.
Antes de iniciar, vamos definir dois conceitos que você vai ver com frequência daqui em diante, vetor de entrada e vetor de pesos:
Vetor de entrada – todos os valores de entrada de cada Perceptron são coletivamente chamados de vetor de entrada desse Perceptron. Esses são seus dados de entrada.
Vetor de pesos – de forma semelhante, todos os valores de peso de cada Perceptron são coletivamente chamados de vetor de peso desse Perceptron. Iniciamos nossa rede neural artificial com valores aleatórios de pesos e durante o treinamento a rede neural aprende os valores de peso ideais. Como veremos, existem muitas formas de realizar esse processo.
Boa parte do trabalho de uma rede neural vai girar em torno das operações algébricas entre o vetor de entrada e o vetor de pesos. Em seguida, vamos adicionando outras camadas matemáticas ou estatísticas para realizar diferentes operações, de acordo com o problema que estamos tentando resolver com o modelo de rede neural. Você vai perceber que tudo não passa de Matemática, que pode ser implementada com linguagens de programação, grandes conjuntos de dados e processamento paralelo, para formar sistemas de Inteligência Artificial.
Mas o que um Perceptron pode fazer afinal?
No capítulo anterior descrevemos os Perceptrons como um método para pesar evidências a fim de tomar decisões. Outra forma em que os Perceptrons podem ser usados é para calcular as funções lógicas elementares tais como AND, OR e NAND (caso tenha dúvidas sobre as operações lógicas, consulte as referências ao final deste capítulo). Por exemplo, suponha que tenhamos um Perceptron com duas entradas, cada uma com peso -2 e um viés de 3. Aqui está o nosso Perceptron:
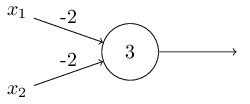
Então vemos que a entrada 00 produziria a saída 1, uma vez que (-2) * 0 + (- 2) * 0 + 3 = 3, é positivo (resultado positivo, gera saída 1 do Perceptron, lembra do capítulo anterior?). Aqui, incluímos o símbolo * para tornar as multiplicações explícitas. Cálculos similares mostram que as entradas 01 e 10 produzem a saída 1. Mas a entrada 11 produz a saída 0, uma vez que (-2) * 1 + (- 2) * 1 + 3 = -1, é negativo. E assim nosso Perceptron implementa um “portão” NAND, ou uma operação lógica binária NAND.
O exemplo NAND mostra que podemos usar Perceptrons para calcular funções lógicas simples. Na verdade, podemos usar redes de Perceptrons para calcular qualquer função lógica. A razão é que o portão NAND é universal para computação, ou seja, podemos construir qualquer computação com portões NAND.
Uma rede de Perceptrons pode ser usada para simular um circuito contendo muitos portões NAND. E como os portões NAND são universais para a computação, segue-se que os Perceptrons também são universais para a computação. Considerando que o Perceptron é o modelo mais simples de rede neural, imagine o que pode ser feito com modelos bem mais avançados! Acertou se você pensou em Inteligência Artificial.
A universalidade computacional dos Perceptrons é simultaneamente reconfortante e decepcionante. É reconfortante porque nos diz que redes de Perceptrons podem ser tão poderosas como qualquer outro dispositivo de computação. Mas também é decepcionante, porque parece que os Perceptrons são meramente um novo tipo de portão NAND. Isso não é uma grande noticia!
No entanto, a situação é melhor do que esta visão sugere. Acontece que podemos conceber algoritmos de aprendizado que podem ajustar automaticamente os pesos e os vieses de uma rede de neurônios artificiais. Este ajuste ocorre em resposta a estímulos externos, sem intervenção direta de um programador. Esses algoritmos de aprendizagem nos permitem usar neurônios artificiais de uma maneira que é radicalmente diferente dos portões lógicos convencionais. Em vez de colocar explicitamente um circuito de NAND e outros portões, nossas redes neurais podem simplesmente aprender a resolver problemas, às vezes problemas em que seriam extremamente difíceis de projetar diretamente usando um circuito convencional de lógica.
Operações Lógicas e Regiões Linearmente Separáveis
Conforme mencionado acima, um Perceptron calcula a soma ponderada dos valores de entrada. Por simplicidade, suponhamos que existem dois valores de entrada, x e y para um certo Perceptron P. Vamos definir os pesos de x e y, como sendo A e B, respectivamente. A soma ponderada pode ser representada como: A x + B y.
Uma vez que o Perceptron produz um valor não-zero somente quando a soma ponderada excede um certo limite C, pode-se escrever a saída deste Perceptron da seguinte maneira:
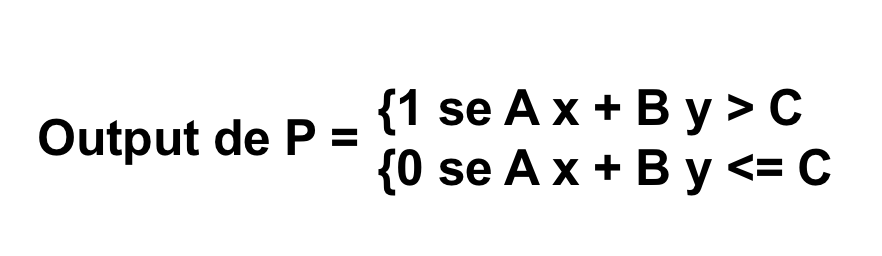
Considerando que A x + B y > C e A x + B y < C são as duas regiões no plano xy separadas pela linha A x + B y + C = 0, e se considerarmos ainda a entrada (x, y) como um ponto em um plano, então o Perceptron realmente nos diz qual região no plano a que esse ponto pertence. Tais regiões, uma vez que são separadas por uma única linha, são chamadas de regiões linearmente separáveis.
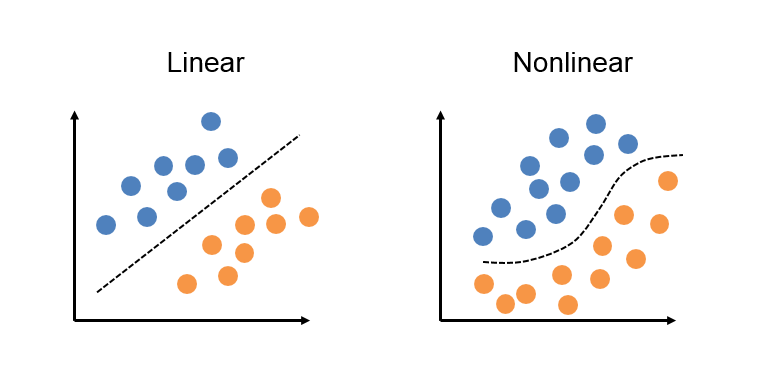
Um único Perceptron consegue resolver somente funções linearmente separáveis. Em funções não linearmente separáveis, o Perceptron não consegue gerar um hiperplano, esta linha nos gráficos abaixo, para separar os dados. A questão é que no mundo real raramente os dados são linearmente separáveis, fazendo com o que o Perceptron não seja muito útil para atividades práticas (mas sendo ideal para iniciar o estudo em redes neurais artificiais). E como separamos os dados não linearmente separáveis? Continue acompanhando este livro e você irá descobrir.
Mas ainda assim o Perceptron tem sua utilidade, porque resulta em algumas funções lógicas, como os operadores booleanos AND, OR e NOT, que são linearmente separáveis, isto é, eles podem ser realizadas usando um único Perceptron. Podemos ilustrar porque eles são linearmente separáveis ao traçar cada um deles em um gráfico:
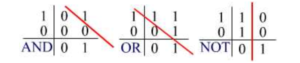
Nos gráficos acima, os dois eixos são as entradas que podem levar o valor de 0 ou 1 e os números no gráfico são a saída esperada para uma entrada específica. Usando um vetor de peso apropriado para cada caso, um único Perceptron pode executar todas essas funções.
No entanto, nem todos os operadores de lógica são linearmente separáveis. Por exemplo, o operador XOR não é linearmente separável e não pode ser alcançado por um único Perceptron. No entanto, esse problema poderia ser superado usando mais de um Perceptron organizado em redes neurais feed-forward, que veremos mais a frente nos próximos capítulos.
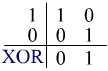
Uma vez que é impossível desenhar uma linha para dividir as regiões contendo 1 ou 0, a função XOR não é linearmente separável, conforme pode ser visto no gráfico acima.
Agora fica mais fácil compreender porque precisamos de arquiteturas mais avançadas de redes neurais artificiais, uma vez que temos problemas complexos no mundo real, como Visão Computacional, Processamento de Linguagem Natural, Tradução, Detecção de Fraudes, Classificação e muitos outros. E veremos essas arquiteturas em detalhes. Mas antes, precisamos falar sobre um componente fundamental das redes neurais, a Função de Ativação. Não perca o próximo capítulo. Até lá.
Referências:
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition
Pattern Recognition and Machine Learning
Redes Neurais, princípios e práticas
Neural Networks and Deep Learning (alguns trechos extraídos e traduzidos com autorização do autor Michael Nielsen)

