Capítulo 34 – O Problema da Dissipação do Gradiente
Então, por que as redes neurais profundas são difíceis de treinar?
Para responder a essa pergunta, primeiro revisitemos o caso de uma rede com apenas uma camada oculta. Como de costume, usaremos o problema de classificação de dígitos MNIST o mesmo já estudado nos capítulos anteriores e que você encontra aqui.
A partir de um shell do Python, nós carregamos os dados MNIST:

Montamos nossa rede:

Esta rede possui 784 neurônios na camada de entrada, correspondendo a 28 × 28 = 784 pixels na imagem de entrada. Utilizamos 30 neurônios ocultos, assim como 10 neurônios de saída, correspondentes às 10 classificações possíveis para os dígitos MNIST (‘0’, ‘1’, ‘2’,…, ‘9’).
Vamos tentar treinar nossa rede por 30 épocas completas, usando mini-lotes de 10 exemplos de treinamento por vez, uma taxa de aprendizado η = 0.1 e um parâmetro de regularização λ = 5.0. À medida que treinarmos, monitoramos a precisão da classificação no conjunto de dados validation_data. Podemos executar o script test.py com todos os comandos. Via prompt de comando ou terminal, digitamos: python test.py (o treinamento pode levar muitos minutos dependendo da velocidade do computador).

Ao final do treinamento, obtemos uma precisão de classificação de 96,48% (aproximadamente), comparável a nossos resultados anteriores com uma configuração semelhante. Agora, vamos adicionar outra camada oculta, também com 30 neurônios, e tentar treinar com os mesmos hiperparâmetros. Usamos:
net = network2.Network([784, 30, 30, 10])
Isto dá uma melhor precisão de classificação 96,90%. Isso é encorajador: um pouco mais de profundidade está ajudando. Vamos adicionar outra camada oculta de 30 neurônios.
net = network2.Network([784, 30, 30, 30, 10])
Isso não ajuda em nada. Na verdade, o resultado cai para 96,57%, próximo à nossa rede original. E suponha que inserimos mais uma camada oculta.
net = network2.Network([784, 30, 30, 30, 30, 10])
Esse comportamento parece estranho. Intuitivamente, camadas ocultas extras devem tornar a rede capaz de aprender funções de classificação mais complexas e, assim, fazer uma melhor classificação. Certamente, as coisas não devem piorar, já que as camadas extras podem, no pior dos casos, simplesmente não fazer nada. Mas não é isso que está acontecendo.
Então, o que está acontecendo? Vamos supor que as camadas ocultas extras realmente possam ajudar em princípio e o problema é que nosso algoritmo de aprendizado não está encontrando os pesos e vieses corretos. Gostaríamos de descobrir o que está errado em nosso algoritmo de aprendizado e como fazer melhor.
Para entender melhor o que está errado, vamos visualizar como a rede aprende. Abaixo, traçamos parte de uma rede [784,30,30,10], ou seja, uma rede com duas camadas ocultas, cada uma contendo 30 neurônios ocultos. Cada neurônio no diagrama tem uma pequena barra nele, representando a rapidez com que o neurônio está mudando à medida que a rede aprende. Uma barra grande significa que o peso e o viés do neurônio estão mudando rapidamente, enquanto uma barra pequena significa que os pesos e o viés estão mudando lentamente. Mais precisamente, as barras indicam o gradiente ∂C / ∂b para cada neurônio, ou seja, a taxa de mudança do custo em relação ao viés do neurônio.
Nos capítulos anteriores, vimos que essa quantidade de gradiente controlava não apenas a rapidez com que o viés muda durante o aprendizado, mas também a rapidez com que os pesos inseridos no neurônio também mudam. Não se preocupe se você não se lembrar dos detalhes: a única coisa a ter em mente é simplesmente que essas barras mostram a rapidez com que os pesos e os vieses de cada neurônio mudam conforme a rede aprende.
Para manter o diagrama simples, mostrei apenas os seis principais neurônios nas duas camadas ocultas. Eu omiti os neurônios de entrada, pois eles não têm pesos nem viés para aprender. Eu também omiti os neurônios de saída, já que estamos fazendo comparações por camadas, e faz mais sentido comparar camadas com o mesmo número de neurônios. Os resultados foram plotados no início do treinamento, ou seja, imediatamente após a inicialização da rede. Aqui estão eles:
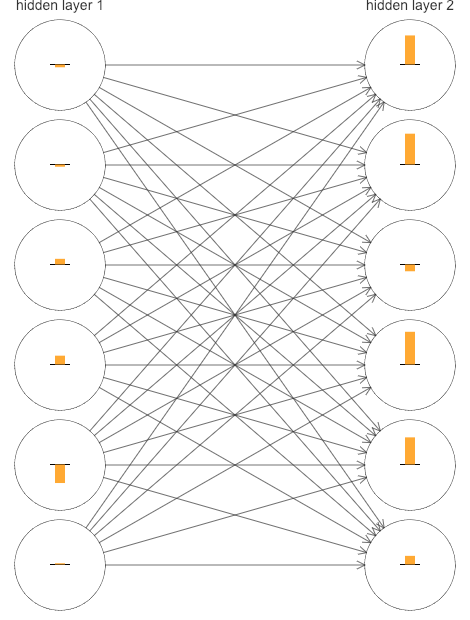
A rede foi inicializada aleatoriamente e, portanto, não é surpreendente que haja muita variação na rapidez com que os neurônios aprendem. Ainda assim, uma coisa que vale ressaltar é que as barras na segunda camada oculta são em sua maioria muito maiores que as barras na primeira camada oculta. Como resultado, os neurônios da segunda camada oculta aprendem um pouco mais rápido que os neurônios da primeira camada oculta. Isso é meramente uma coincidência, ou os neurônios da segunda camada oculta provavelmente aprenderão mais rápido do que os neurônios na primeira camada oculta em geral?
Para determinar se esse é o caso, é útil ter uma maneira global de comparar a velocidade de aprendizado na primeira e segunda camadas ocultas. Para fazer isso, vamos indicar o gradiente como δlj = ∂C / ∂blj, ou seja, o gradiente para o neurônio jth na camada lth.
Podemos pensar no gradiente δ1 como um vetor cujas entradas determinam a rapidez com que a primeira camada oculta aprende, e δ2 como um vetor cujas entradas determinam a rapidez com que a segunda camada oculta aprende. Em seguida, usaremos os comprimentos desses vetores como medidas globais da velocidade na qual as camadas estão aprendendo. Assim, por exemplo, o comprimento “δ1” mede a velocidade na qual a primeira camada oculta está aprendendo, enquanto o comprimento “δ2” mede a velocidade na qual a segunda camada oculta está aprendendo.
Com essas definições, e na mesma configuração que foi plotada acima, encontramos δδ1 = 0.07… e δδ2 = 0.31…. Isso confirma nossa suspeita anterior: os neurônios na segunda camada oculta realmente estão aprendendo muito mais rápido que os neurônios da primeira camada oculta.
O que acontece se adicionarmos mais camadas ocultas? Se tivermos três camadas ocultas, em uma rede [784,30,30,30,10], então as respectivas velocidades de aprendizado serão 0,012, 0,060 e 0,283. Novamente, as camadas ocultas anteriores estão aprendendo muito mais lentamente que as camadas ocultas posteriores. Suponha que adicionemos mais uma camada com 30 neurônios ocultos. Nesse caso, as respectivas velocidades de aprendizado são 0,003, 0,017, 0,070 e 0,285. O padrão é válido: as camadas iniciais aprendem mais lentamente que as camadas posteriores.
Temos observado a velocidade de aprendizado no início do treinamento, ou seja, logo após as redes serem inicializadas. Como a velocidade do aprendizado muda à medida que treinamos nossas redes? Vamos voltar para ver a rede com apenas duas camadas ocultas. A velocidade de aprendizado muda da seguinte forma:
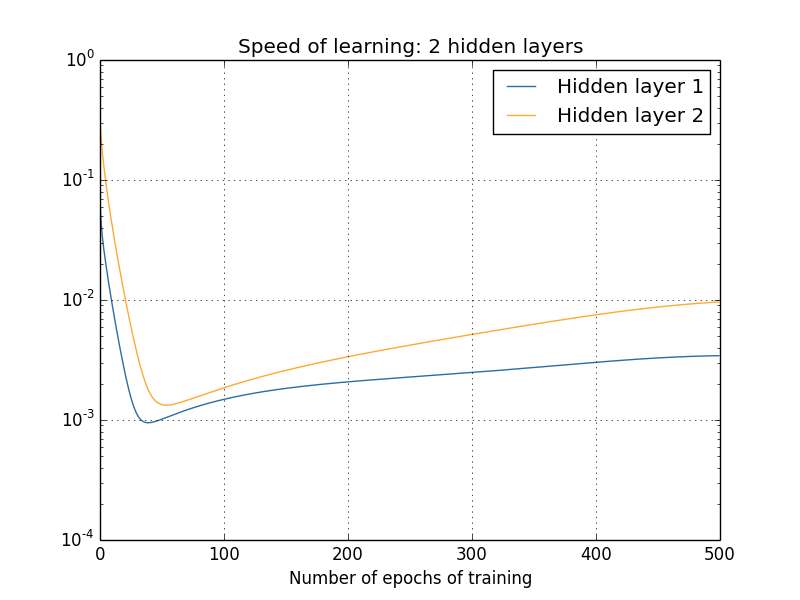
Para gerar esses resultados, usamos a descida do gradiente em lote com apenas 1.000 imagens de treinamento, treinadas em mais de 500 épocas. Isso é um pouco diferente do que normalmente treinamos nos capítulos anteriores, mas acontece que o uso de gradiente estocástico em mini-lote dá resultados muito mais ruidosos (embora muito similares, quando você mede o ruído). Usar os parâmetros que escolhemos é uma maneira fácil de suavizar os resultados, para que possamos ver o que está acontecendo.
Em qualquer caso, como você pode ver, as duas camadas começam a aprender em velocidades muito diferentes (como já sabemos). A velocidade em ambas as camadas cai muito rapidamente, antes de se recuperar. Mas, apesar de tudo, a primeira camada oculta aprende muito mais lentamente do que a segunda camada oculta.
E quanto a redes mais complexas? Aqui estão os resultados de uma experiência semelhante, mas desta vez com três camadas ocultas (uma rede [784,30,30,30,10]):
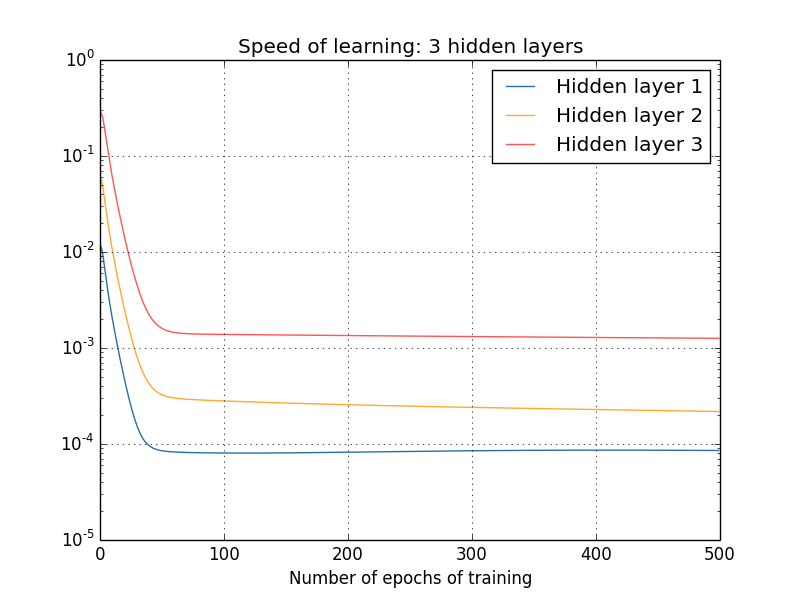
Mais uma vez, as primeiras camadas ocultas aprendem muito mais lentamente do que as camadas ocultas posteriores. Finalmente, vamos adicionar uma quarta camada oculta (uma rede [784,30,30,30,30,10]) e ver o que acontece quando treinamos:
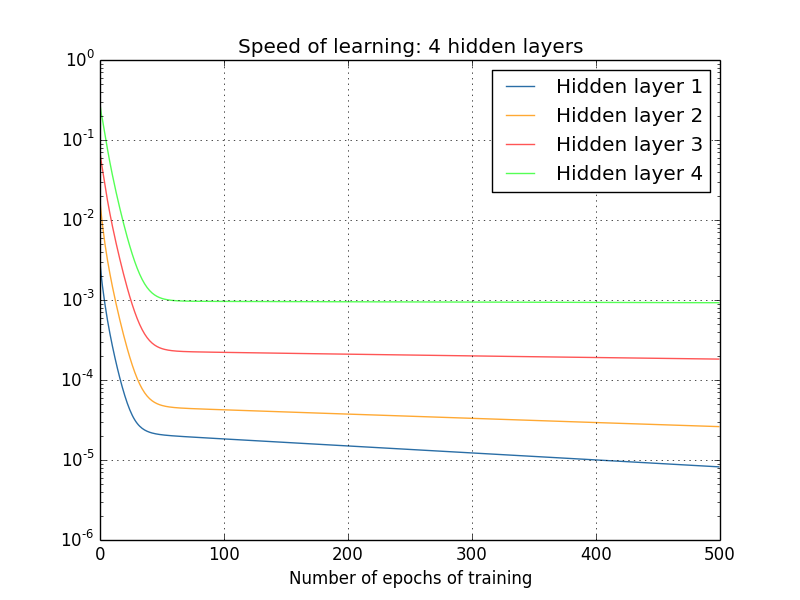
Mais uma vez, as primeiras camadas ocultas aprendem muito mais lentamente do que as camadas ocultas posteriores. Nesse caso, a primeira camada oculta está aprendendo aproximadamente 100 vezes mais lenta que a camada oculta final. Natural que estivéssemos tendo problemas para treinar essas redes antes!
Temos aqui uma observação importante: em pelo menos algumas redes neurais profundas, o gradiente tende a diminuir à medida que nos movemos para trás através das camadas ocultas. Isso significa que os neurônios nas camadas anteriores aprendem muito mais lentamente que os neurônios nas camadas posteriores. E, embora tenhamos visto isso em apenas uma única rede, há razões fundamentais pelas quais isso acontece em muitas redes neurais. O fenômeno é conhecido como O Problema da Dissipação do Gradiente ou The Vanishing Gradient Problem. Esse é um problema muito comum e ainda mais evidente em Redes Neurais Recorrentes, usadas em aplicações de Processamento de Linguagem Natural.
Por que o problema de dissipação do gradiente ocorre? Existem maneiras de evitar isso? E como devemos lidar com isso no treinamento de redes neurais profundas? Na verdade, aprenderemos rapidamente que não é inevitável, embora a alternativa também não seja muito atraente: às vezes, o gradiente fica muito maior nas camadas anteriores! Este problema é chamado de explosão do gradiente, e não é uma notícia muito melhor do que o problema da dissipação do gradiente. Geralmente, verifica-se que o gradiente em redes neurais profundas é instável, tendendo a explodir ou a desaparecer nas camadas anteriores. Essa instabilidade é um problema fundamental para o aprendizado baseado em gradiente em redes neurais profundas. É algo que precisamos entender e, se possível, tomar medidas para resolver.
Momentaneamente se afastando das redes neurais, imagine que estamos tentando minimizar numericamente uma função f(x) de uma única variável. Não seria uma boa notícia se a derivada f′(x) fosse pequena? Isso não significaria que já estávamos perto de um extremo? De forma semelhante, o pequeno gradiente nas primeiras camadas de uma rede profunda pode significar que não precisamos fazer muito ajuste dos pesos e vieses?
Claro, isso não é o caso. Lembre-se de que inicializamos aleatoriamente o peso e os vieses na rede. É extremamente improvável que nossos pesos e vieses iniciais façam um bom trabalho em qualquer coisa que desejamos que nossa rede faça. Para ser concreto, considere a primeira camada de pesos em uma rede [784,30,30,30,10] para o problema MNIST.
A inicialização aleatória significa que a primeira camada elimina a maior parte das informações sobre a imagem de entrada. Mesmo que as camadas posteriores tenham sido extensivamente treinadas, elas ainda acharão extremamente difícil identificar a imagem de entrada, simplesmente porque elas não possuem informações suficientes. E assim, não é possível que não seja preciso aprender muito na primeira camada. Se vamos treinar redes profundas, precisamos descobrir como resolver o problema da dissipação do gradiente.
Se eu fosse você, não perderia o próximo capítulo com uma explicação matemática para esse importante fenômeno no treinamento de redes neurais profundas (Deep Learning).
Referências:
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning (material usado com autorização do autor)
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

