Capítulo 36 – Outros Problemas com o Gradiente em Redes Neurais Artificiais
No capítulo anterior descrevemos para você a Matemática que ajuda a explicar a causa do problema da dissipação do gradiente. Mas a dissipação não é o único problema que pode ocorrer. Neste capítulo vamos descrever outros possíveis problemas com o gradiente em redes neurais artificiais.
Explosão do Gradiente
Vamos ver um exemplo explícito em que ocorre a explosão dos gradientes. O exemplo é bem simples e vamos alterar alguns parâmetros na rede de maneira a garantir que tenhamos a explosão do gradiente. Mesmo fazendo essa alteração para forçar o problema, a explosão do gradiente não é apenas uma possibilidade hipotética e realmente pode acontecer.
Há duas etapas para obter a explosão do gradiente. Primeiro, escolhemos todos os pesos na rede como grandes, digamos w1 = w2 = w3 = w4 = 100. Segundo, vamos escolher os vieses para que os termos σ ′ (zj) não sejam muito pequenos. Isso é realmente muito fácil de fazer: tudo o que precisamos é escolher os vieses para garantir que a entrada ponderada para cada neurônio seja zj = 0 (e então σ ′ (zj) = 1/4). Então, por exemplo, queremos z1 = w1a0 + b1 = 0. Podemos conseguir isso ajustando b1 = −100 ∗ a0. Podemos usar a mesma ideia para selecionar os outros vieses. Quando fazemos isso, vemos que todos os termos wjσ ′ (zj) são iguais a 100 ∗ 1/4 = 25. Com estas escolhas ocorre o problema da explosão do gradiente.
Instabilidade do Gradiente
O problema fundamental aqui não é tanto o problema do gradiente que desaparece ou o problema do gradiente que explode. É que o gradiente nas camadas iniciais é o produto dos termos de todas as camadas posteriores. Quando há muitas camadas, essa é uma situação intrinsecamente instável. A única maneira que todas as camadas podem aprender perto da mesma velocidade é se todos esses produtos de termos estiverem próximos de se equilibrar. Sem algum mecanismo ou razão subjacente para que o equilíbrio ocorra, é altamente improvável que aconteça simplesmente por acaso. Em suma, o problema real aqui é que as redes neurais sofrem de um problema de instabilidade do gradiente. Como resultado, se usarmos técnicas de aprendizado baseadas em gradiente padrão, camadas diferentes na rede tenderão a aprender em velocidades totalmente diferentes.
O Problema Mais Comum é Mesmo a Dissipação do Gradiente
Vimos que o gradiente pode desaparecer ou explodir nas camadas iniciais de uma rede profunda. De fato, ao usar neurônios sigmóides, o gradiente geralmente desaparece. Para ver porque, considere novamente a expressão | wσ ′ (z) |. Para evitar o problema da dissipação do gradiente, precisamos | wσ ′ (z) | ≥1. Você pode pensar que isso pode acontecer facilmente se w for muito grande. No entanto, é mais difícil do que parece. A razão é que o termo σ ′ (z) também depende de w: σ ′ (z) = σ ′ (wa + b), onde a é a ativação da entrada.
Então, quando fazemos w grande, precisamos ter cuidado para que não tornemos simultaneamente σ ′ (wa + b) pequeno. Isso acaba sendo uma restrição considerável. A razão é que quando fazemos w grande, tendemos a tornar o wa + b muito grande. Olhando para um gráfico de σ ′ você pode ver que isso nos coloca fora das “asas” da função σ ′, onde é preciso valores muito pequenos. A única maneira de evitar isso é se a ativação de entrada estiver dentro de um intervalo bastante estreito de valores. Às vezes isso vai acontecer, mas frequentemente, porém, isso não acontece. E assim, no caso genérico, temos a dissipação dos gradientes.
Gradientes Instáveis em Redes Mais Complexas
Temos estudado redes simples como exemplo, com apenas um neurônio em cada camada oculta. E quanto a redes profundas mais complexas, com muitos neurônios em cada camada oculta (tipicamente Deep Learning)?
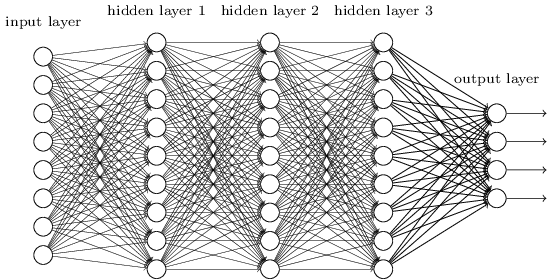
De fato, o mesmo comportamento ocorre em tais redes. Nos capítulos anteriores onde estudamos retropropagação, vimos que o gradiente na camada l de uma rede de camada L é dado por:
![]()
Aqui, Σ ′ (zl) é uma matriz diagonal cujas entradas são os valores σ ′ (z) para as entradas ponderadas para a camada l. As wl são as matrizes de peso para as diferentes camadas. E ∇aC é o vetor de derivadas parciais de C em relação às ativações de saída.
Essa é uma expressão muito mais complicada do que no caso de um único neurônio. Ainda assim, se você olhar de perto, a forma essencial é muito semelhante, com muitos pares da forma:
![]()
Além disso, as matrizes Σ′ (zj) possuem pequenas entradas na diagonal, nenhuma maior que 1/4. Desde que as matrizes de peso wj não sejam muito grandes, cada termo adicional:![]()
tende a fazer o vetor gradiente menor, levando a uma dissipação do gradiente. Mais genericamente, o grande número de termos no produto tende a levar a um gradiente instável, assim como no nosso exemplo anterior. Na prática isso é tipicamente encontrado em redes sigmóides que os gradientes desaparecem exponencialmente de forma rápida nas camadas anteriores. Como resultado, o aprendizado diminui nessas camadas. Essa desaceleração não é apenas um acidente ou uma inconveniência: é uma consequência fundamental da abordagem que estamos adotando para o aprendizado da rede.
Outros Obstáculos Para a Aprendizagem Profunda
Nestes últimos capítulos, nos concentramos na dissipação de gradientes – e, em geral, gradientes instáveis – como um obstáculo à aprendizagem profunda. De fato, gradientes instáveis são apenas um obstáculo para o aprendizado profundo, embora seja um importante obstáculo fundamental. Muitas pesquisas em andamento têm como objetivo entender melhor os desafios que podem ocorrer quando se treinam redes profundas. Vamos mencionar brevemente alguns artigos, para dar a você o sabor de algumas das perguntas que as pessoas estão fazendo.
Como primeiro exemplo, em 2010 Glorot e Bengio encontraram evidências sugerindo que o uso de funções de ativação sigmóide pode causar problemas ao treinamento de redes profundas. Em particular, eles encontraram evidências de que o uso de sigmóides fará com que as ativações na camada oculta final saturem perto de 0 no início do treinamento, diminuindo substancialmente o aprendizado. Eles sugeriram algumas funções de ativação alternativas, que parecem não sofrer tanto com esse problema de saturação.
Como um segundo exemplo, em 2013, Sutskever, Martens, Dahl e Hinton estudaram o impacto na aprendizagem profunda tanto da inicialização de peso aleatório quanto do cronograma de momentum na descida de gradiente estocástica baseada no momento. Em ambos os casos, fazer boas escolhas fez uma diferença substancial na capacidade de treinar redes profundas.
Esses exemplos sugerem que “O que dificulta o treinamento de redes profundas?” é uma questão complexa. Nestes últimos capítulos, nos concentramos nas instabilidades associadas ao aprendizado baseado em gradiente em redes profundas. Os resultados dos dois últimos parágrafos sugerem que há também um papel desempenhado pela escolha da função de ativação, a forma como os pesos são inicializados e até mesmo detalhes de como a aprendizagem por gradiente descendente é implementada. E, claro, a escolha da arquitetura de rede e outros hiperparâmetros também é importante. Assim, muitos fatores podem desempenhar um papel em dificultar a formação de redes profundas, e a compreensão de todos esses fatores ainda é objeto de pesquisas em andamento. A boa notícia é que, a partir do próximo capítulo, vamos mudar isso e desenvolver várias abordagens para o aprendizado profundo que, até certo ponto, conseguem superar ou direcionar todos esses desafios.
Não é incrível o que estamos vivenciando neste exato momento da história humana? Tudo isso que estudamos até aqui forma a base de aplicações de Inteligência Artificial que já são encontradas no mercado, em diversas aplicações e até mesmo em nossos smartphones. E ainda estamos apenas no começo.
E você, quer ou não fazer parte desta incrível revolução trazida pela Inteligência Artificial? Se a resposta for sim, o que está esperando?
Referências:
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning (material usado com autorização do autor)
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

