Capítulo 33 – Por que as Redes Neurais Profundas São Difíceis de Treinar?
Iniciamos agora a terceira e última parte deste livro, em que estudaremos como funciona Deep Learning e os principais modelos e arquiteturas de redes neurais profundas, com diversos exemplos e aplicações. Mas primeiro temos que responder a seguinte pergunta: Por que as Redes Neurais Profundas São Difíceis de Treinar?
Imagine que você é um engenheiro que foi solicitado a projetar um computador do zero. Um dia, você está trabalhando em seu escritório, projetando circuitos lógicos, estabelecendo portas AND e OU, e assim por diante, quando seu chefe chega com más notícias. O cliente acaba de adicionar um requisito de design surpreendente: o circuito para o computador inteiro deve ter apenas duas camadas de profundidade:
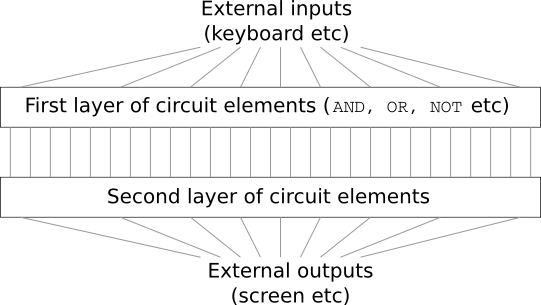
Você fica estupefato e diz ao seu chefe: “O cliente está louco!”
Seu chefe responde: “Eu acho que eles são loucos também. Mas precisamos atender este requisito.”
Na verdade, há um sentido limitado em que o cliente não é louco. Suponha que você tenha permissão para usar uma porta lógica especial que permite a você aplicar o AND (o “e” da lógica) e juntar quantas entradas desejar. E você também tem permissão para uma porta NAND com muitas entradas, ou seja, uma porta que pode aplicar o AND a várias entradas e depois nega a saída. Com essas portas especiais, é possível calcular qualquer função usando um circuito com apenas duas camadas de profundidade.
Mas só porque algo é possível, não é uma boa ideia. Na prática, quando resolvemos problemas de projeto de circuitos (ou quase todos os tipos de problemas algorítmicos), geralmente começamos descobrindo como resolver sub-problemas, e então gradualmente integramos as soluções. Em outras palavras, criamos uma solução através de várias camadas de abstração.
Por exemplo, suponha que estamos projetando um circuito lógico para multiplicar dois números. Provavelmente, queremos construí-lo a partir de sub-circuitos, fazendo operações como adicionar dois números. Os sub-circuitos para adicionar dois números serão, por sua vez, construídos a partir de sub-sub-circuitos para adicionar dois bits. Muito grosso modo, nosso circuito será parecido com:
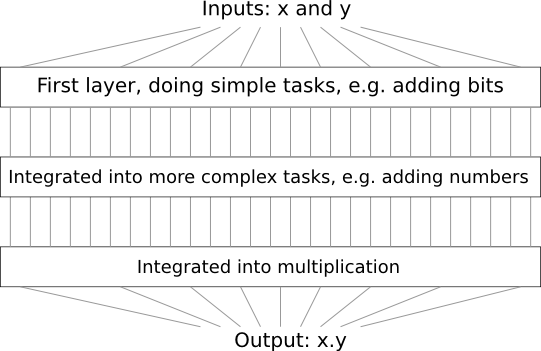
Ou seja, nosso circuito final contém pelo menos três camadas de elementos de circuito. Na verdade, provavelmente conterá mais de três camadas, pois dividimos as sub-tarefas em unidades menores do que as descritas anteriormente. Mas você compreendeu a ideia geral.
Então circuitos profundos facilitam o processo de design. Mas eles não são apenas úteis para o design. Existem, de fato, provas matemáticas mostrando que, para algumas funções, circuitos muito superficiais requerem exponencialmente mais elementos de circuitos para serem computados do que circuitos profundos. Por exemplo, uma famosa série de artigos no início dos anos 1980 mostrou que calcular a paridade de um conjunto de bits requer muitos portões exponencialmente, se feito com um circuito superficial.
Por outro lado, se você usa circuitos mais profundos, é fácil calcular a paridade usando um pequeno circuito: basta calcular a paridade de pares de bits, depois usar esses resultados para calcular a paridade de pares de pares de bits e assim por diante. construindo rapidamente a paridade geral. Os circuitos profundos, portanto, podem ser intrinsecamente muito mais poderosos que os circuitos superficiais.
Até agora, este livro abordou redes neurais como o cliente louco. Quase todas as redes com as quais trabalhamos têm apenas uma camada oculta de neurônios (mais as camadas de entrada e saída):
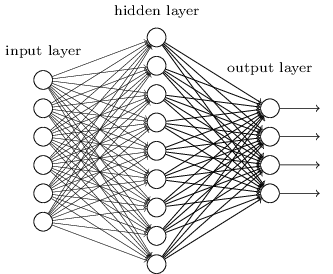
Essas redes simples têm sido extraordinariamente úteis: nos capítulos anteriores, usamos redes como essa para classificar dígitos manuscritos com precisão superior a 98%! No entanto, intuitivamente, esperamos que as redes com muito mais camadas ocultas sejam mais poderosas:
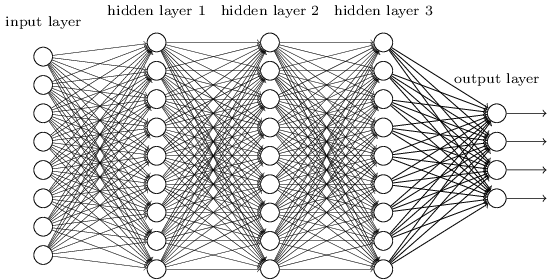
Tais redes poderiam usar as camadas intermediárias para construir múltiplas camadas de abstração, assim como fazemos em circuitos booleanos. Por exemplo, se estamos fazendo reconhecimento de padrões visuais, então os neurônios da primeira camada podem aprender a reconhecer bordas, os neurônios da segunda camada podem aprender a reconhecer formas mais complexas, digamos, triângulo ou retângulos, construídos a partir de bordas. A terceira camada reconheceria formas ainda mais complexas. E assim por diante. Essas múltiplas camadas de abstração parecem propiciar às redes profundas uma vantagem convincente em aprender a resolver problemas complexos de reconhecimento de padrões. Além disso, assim como no caso dos circuitos, existem resultados teóricos sugerindo que as redes profundas são intrinsecamente mais poderosas do que as redes superficiais.
Como podemos treinar essas redes profundas? Nos próximos capítulos, tentaremos treinar redes profundas usando nosso algoritmo de aprendizado: descendente de gradiente estocástico por retropropagação (que já estudamos em detalhes nos capítulos anteriores, mas que agora aplicaremos em redes neurais profundas). Mas vamos nos deparar com problemas, com nossas redes profundas não realizando muito (se for o caso) melhor do que redes rasas.
Essa falha parece surpreendente à luz da discussão acima. Em vez de desistir de redes profundas, vamos nos aprofundar e tentar entender o que está dificultando o treinamento de nossas redes profundas. Quando olharmos de perto, descobriremos que as diferentes camadas da nossa rede profunda estão aprendendo em velocidades muito diferentes.
Em particular, quando as camadas posteriores da rede estão aprendendo bem, as camadas iniciais geralmente ficam presas durante o treinamento, aprendendo quase nada. Este empecilho não é simplesmente devido à má sorte. Em vez disso, descobriremos que existem razões fundamentais para a lentidão do aprendizado, conectadas ao nosso uso de técnicas de aprendizado baseadas em gradientes.
À medida que nos aprofundamos no problema, aprenderemos que o fenômeno oposto também pode ocorrer: as primeiras camadas podem estar aprendendo bem, mas as camadas posteriores podem ficar presas. Na verdade, descobriremos que existe uma instabilidade intrínseca associada ao aprendizado por gradiente descendente em redes neurais profundas de muitas camadas. Essa instabilidade tende a resultar em camadas anteriores ou posteriores ficando presas durante o treinamento.
Mas, ao nos debruçarmos sobre essas dificuldades, podemos começar a entender o que é necessário para treinar redes profundas de maneira eficaz. E isso é exatamente o que faremos nos próximos capítulos.
Agora é que começa a diversão. Até lá.
Referências:
Análise Estatística Para Data Science com Linguagem Python
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

