Capítulo 39 – Relação Entre o Tamanho do Lote e o Cálculo do Gradiente
Vamos continuar com a discussão dos dois capítulos anteriores e investigar a Relação Entre o Tamanho do Lote e o Cálculo do Gradiente.
Como explicar porque o treinamento com lotes maiores leva a uma precisão menor nos testes? Uma hipótese pode ser que as amostras de treinamento no mesmo lote interfiram (competem) com o gradiente um do outro. Uma amostra deseja mover os pesos do modelo em uma direção, enquanto outra amostra deseja mover os pesos na direção oposta. Portanto, seus gradientes tendem a ser cancelados e você obtém um pequeno gradiente geral. Talvez, se as amostras forem divididas em dois lotes, a concorrência será reduzida, pois o modelo poderá encontrar pesos que satisfarão as duas amostras, se forem feitas em sequência. Em outras palavras, a otimização sequencial de amostras é mais fácil do que a otimização simultânea em espaços de parâmetros complexos e de alta dimensão.
A hipótese é representada graficamente abaixo. A seta lilás mostra um único degrau de gradiente descendente usando um tamanho de lote de 2. As setas azul e vermelha mostram duas etapas sucessivas de descida do gradiente usando um tamanho de lote 1. A seta preta é a soma vetorial das setas azul e vermelha e representa o progresso geral que o modelo faz em duas etapas de tamanho de lote 1. Ambos os experimentos começam com os mesmos pesos no espaço de pesos. Embora não seja explicitamente mostrado na imagem, a hipótese é que a linha lilás é muito mais curta que a linha preta, devido à concorrência dos gradientes. Em outras palavras, o gradiente de uma única etapa de tamanho de lote grande é menor que a soma de gradientes de várias etapas de tamanho de lote pequeno.
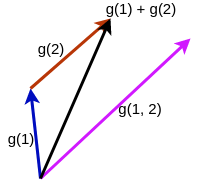
O experimento envolve a replicação da imagem mostrada acima. Nós treinamos o modelo para um determinado estado. Em seguida, o grupo de controle (seta lilás) é calculado encontrando o gradiente de etapa única com tamanho de lote 1024. O grupo experimental (seta preta) é calculado fazendo várias etapas de gradiente e encontrando a soma vetorial desses gradientes usando um tamanho de lote menor. O produto do número de etapas e do tamanho do lote é constante em 1024. Isso representa modelos diferentes que veem um número fixo de amostras.
Por exemplo, para um tamanho de lote de 64, fazemos 1024/64 = 16 etapas, somando os 16 gradientes para encontrar o gradiente geral. Para tamanho de lote 1024, fazemos 1024/1024 = 1 passo. Observe que, para os tamanhos de lote menores, amostras diferentes são desenhadas para cada lote. A ideia é comparar os gradientes do modelo para diferentes tamanhos de lotes após os modelos terem visto o mesmo número de amostras. Como última advertência, para simplificar, apenas medimos o gradiente da última camada do nosso modelo MLP (Multilayer Perceptron), que possui 1024 ⋅ 10 = 10240 pesos.
Investigamos os seguintes tamanhos de lote: 1, 2, 3, 4, 5, 6, 7, 8, 16, 32, 64, 128, 256, 512, 1024.
Um teste significou:
- Carregamento / redefinição dos pesos do modelo para um ponto treinado fixo (usamos os pesos do modelo após o treinamento para 2/30 epochs em tamanho de lote 1024).
- Amostragem aleatória de 1024 amostras de dados do conjunto de treinamento.
- Treinamento do modelo através de todas as 1024 amostras de dados uma vez, com diferentes tamanhos de lote.
Para cada tamanho de lote, repetimos o experimento mil vezes. Não coletamos mais dados porque armazenar os tensores de gradiente é realmente muito caro (mantivemos os tensores de cada tentativa para computar estatísticas de ordem mais alta mais tarde). O tamanho total do arquivo com tensores de gradiente foi de 600 MB.
Para cada um dos 1000 ensaios, computamos a norma euclidiana do tensor de gradiente somado (seta preta na nossa imagem). Então, calculamos a média e o desvio padrão dessas normas ao longo dos 1000 testes. Isso é feito para cada tamanho de lote.
Eu queria investigar dois regimes de peso diferentes: no início do treinamento, quando os pesos não convergiam e muito aprendizado ocorria e, mais tarde, durante o treinamento, quando os pesos quase convergiam e o aprendizado mínimo estava ocorrendo. Para o regime inicial, eu treinei o modelo MLP para 2 épocas com tamanho de lote 1024 e para o regime posterior, eu treinei o modelo por 30 épocas.
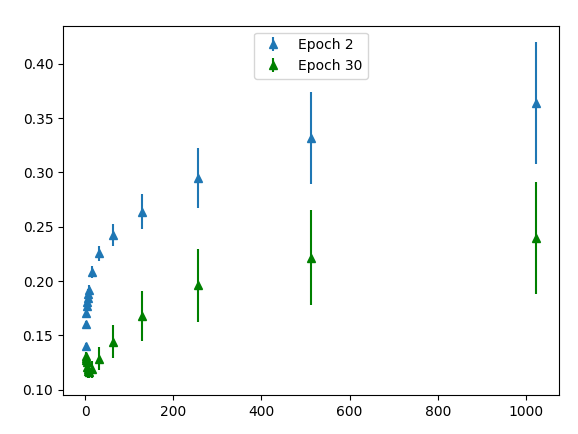
Descoberta: tamanhos de lotes maiores produzem etapas de gradiente maiores do que tamanhos de lotes menores para o mesmo número de amostras vistas.
O eixo x mostra o tamanho do lote. O eixo y mostra a norma euclidiana média de tensores de gradiente em 1000 tentativas. As barras de erro indicam a variação da norma euclidiana em 1000 tentativas. Os pontos azuis é o experimento realizado no regime inicial, onde o modelo foi treinado por 2 épocas. Os pontos verdes é o regime posterior em que o modelo foi treinado por 30 épocas. Como esperado, o gradiente é maior no início do treinamento (os pontos azuis são maiores que os pontos verdes).
Ao contrário da nossa hipótese, a norma gradiente média aumenta com o tamanho do lote! Esperávamos que os gradientes fossem menores para um tamanho de lote maior devido à competição entre as amostras de dados. Em vez disso, o que encontramos é que tamanhos maiores de lotes fazem etapas de gradiente maiores do que tamanhos de lote menores para o mesmo número de amostras vistas. Observe que a norma euclidiana pode ser interpretada como a distância euclidiana entre o novo conjunto de pesos e o conjunto inicial de pesos. Portanto, o treinamento com lotes grandes tende a se afastar dos pesos iniciais depois de ver um número fixo de amostras do que o treinamento com tamanhos de lote menores. A relação entre o tamanho do lote e a norma de gradiente é √x. Em outras palavras, a relação entre o tamanho do lote e a norma do gradiente quadrado é linear.
Além disso, a variação é muito menor para tamanhos menores de lotes. No entanto, o que podemos nos interessar é a magnitude da variância em relação à magnitude da média. Portanto, para fazer uma comparação mais perspicaz, dimensiono a média e o desvio padrão de cada tamanho de lote para a média do tamanho do lote 1024. Em outras palavras,
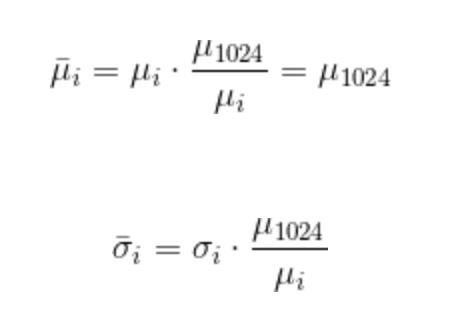
onde as barras representam valores normalizados e i indica um determinado tamanho de lote.
Justificamos o dimensionamento da média e do desvio padrão da norma de gradiente porque isso é equivalente a aumentar a taxa de aprendizado para o experimento com tamanhos de lote menores. Essencialmente, queremos saber “pela mesma distância afastada dos pesos iniciais, qual é a variação nas normas de gradiente para diferentes tamanhos de lote”? Tenha em mente que estamos medindo a variação nas normas de gradiente e não a variação nos gradientes em si, que é uma métrica muito mais precisa.
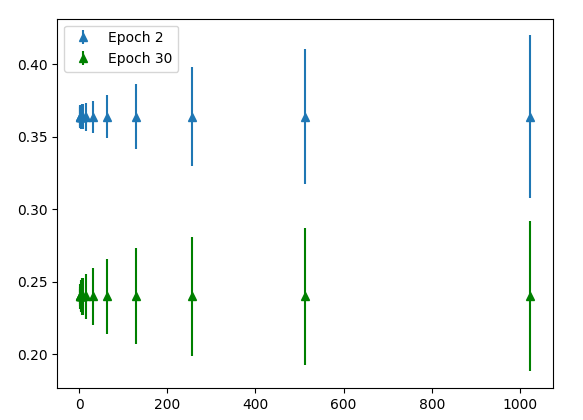
Descoberta: Para a mesma distância média da norma euclidiana dos pesos iniciais do modelo, tamanhos de lote maiores têm maior variância na distância.
Nós vemos um resultado muito surpreendente acima. Para a mesma distância média da norma euclidiana dos pesos iniciais do modelo, tamanhos de lote maiores têm maior variância na distância. Isso é bastante! Em suma, dados dois modelos treinados com tamanhos de lotes diferentes, em qualquer gradiente em particular, se a taxa de aprendizado for ajustada de modo que ambos os modelos se movam em média na mesma distância, o modelo com o tamanho maior do lote variará mais em relação a sua movimentação. Isso é um pouco contra-intuitivo, pois é bem conhecido que tamanhos menores de lotes são “ruidosos” e, portanto, você pode esperar que a variação da norma de gradiente seja maior.
Observe que, para cada teste, estamos usando 1024 amostras diferentes, em vez de usar as mesmas 1024 amostras em todos os testes. Observe também que a variação entre os testes pode ser causada por duas coisas: as diferentes amostras que são extraídas do conjunto de dados entre os diferentes testes e a semente aleatória para cada teste (que não foi controlada, mas deve realmente ser). Seguindo em frente, vou supor que a variação é causada pelo primeiro fator: amostras diferentes. Este é um resultado interessante e poderíamos seguir esta investigação por muitos capítulos. Mas por hora, você já recebeu informação suficiente para compreender a Relação Entre o Tamanho do Lote e o Cálculo do Gradiente. Esse tipo de experimento é muito importante em trabalhos de pesquisa e desenvolvimento de novos modelos!
Podemos assim concluir mais uma etapa deste livro e começar nossa última e mais emocionante jornada de aprendizagem, estudando as principais arquiteturas de Deep Learning. Eu não perderia se fosse você! Até o próximo capítulo!
Referências:
Formação Engenheiro de Inteligência Artificial
Don’t Decay the Learning Rate, Increase the Batch Size
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Effect of batch size on training dynamics
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition

