Capítulo 30 – Variações do Stochastic Gradient Descent – Hessian Optimization e Momentum
Cada técnica mostrada até aqui é valiosa e deve ser dominada por aqueles que pretendem trabalhar com redes neurais artificiais e aplicações de Inteligência Artificial, mas essa não é a única razão pela qual nós as explicamos.
O ponto principal é familiarizar você com alguns dos problemas que podem ocorrer nas redes neurais e com um estilo de análise que pode ajudar a superar esses problemas. De certo modo, aprendemos a pensar sobre redes neurais.
Agora neste capítulo, esquematizamos brevemente algumas outras técnicas. Esses esboços são menos aprofundados do que as discussões anteriores, mas devem transmitir algum sentimento pela diversidade de técnicas disponíveis para uso em redes neurais. Lembrando que você sempre pode estudar todas essas técnicas em detalhes nos cursos da Formação Engenheiro de Inteligência Artificial.
Variações do Stochastic Gradient Descent
A descida de gradiente estocástico pela retropropagação tem nos servido bem no ataque ao problema de classificação de dígitos do dataset MNIST. No entanto, existem muitas outras abordagens para otimizar a função de custo e, às vezes, essas outras abordagens oferecem desempenho superior ao gradiente estocástico em mini-lote. Neste capítulo discutiremos duas dessas abordagens, Hessian Optimization e Momentum.
Hessian Optimization
Para iniciar nossa discussão, ajuda a colocar as redes neurais de lado por um tempo. Em vez disso, vamos apenas considerar o problema abstrato de minimizar uma função de custo C que é uma função de muitas variáveis, w = w1, w2,…, então C = C(w). Pelo teorema de Taylor, a função custo pode ser aproximada perto de um ponto w por:
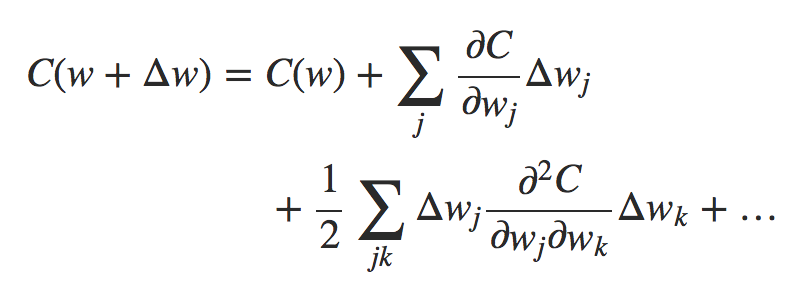
Fórmula 1
Podemos reescrever isso de forma mais compacta:
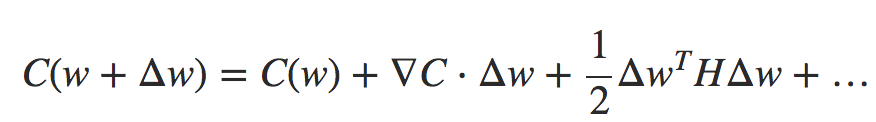
Fórmula 2
onde ∇C é o vetor gradiente usual e H é uma matriz conhecida como Matriz Hessiana. Suponha que nós aproximemos C descartando os termos de ordem superior representados por … acima:
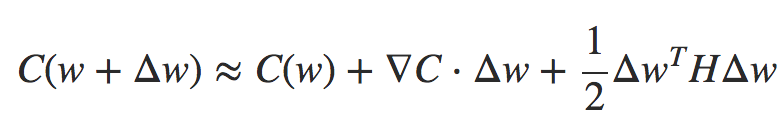
Fórmula 3
Usando o cálculo, podemos mostrar que a expressão do lado direito pode ser minimizada escolhendo:
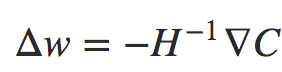
Fórmula 4
Considerando que a Fórmula 3 é uma boa expressão aproximada para a função custo, então esperamos que a mudança do ponto w para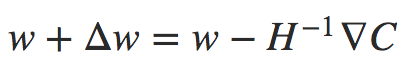 
deva diminuir significativamente a função custo. Isso sugere um algoritmo possível para minimizar o custo:
- Escolha um ponto de partida, w.
- Atualize w para um novo ponto w ′ = w − H ^ − 1 ∇C, onde o Hessian H e ∇C são calculados em w.
- Atualize w′ para um novo ponto w′′ = w′ − H′ ^ − 1 ∇′C, onde o Hessian H′ e ∇′C são calculados em w′.
…
Na prática, a Fórmula 3 é apenas uma aproximação e é melhor dar passos menores. Fazemos isso alterando repetidamente w por uma quantidade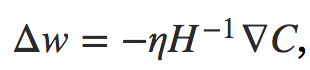 
onde η é conhecido como taxa de aprendizado.
Essa abordagem para minimizar uma função de custo é conhecida como Hessian Technique ou Hessian Optimization. Existem resultados teóricos e empíricos mostrando que os métodos de Hessian convergem em um mínimo em menos etapas do que a descida de gradiente padrão. Em particular, ao incorporar informações sobre mudanças de segunda ordem na função de custo, é possível que a abordagem Hessiana evite muitas patologias que podem ocorrer na descida de gradiente. Além disso, há versões do algoritmo de retropropagação que podem ser usadas para computar o Hessian.
Se a Hessian Optimization é tão bom, por que não a estamos usando em nossas redes neurais? Infelizmente, embora tenha muitas propriedades desejáveis, tem uma propriedade muito indesejável: é muito difícil de aplicar na prática. Parte do problema é o tamanho da matriz Hessiana. Suponha que você tenha uma rede neural com 107 pesos e vieses. Em seguida, a matriz Hessiana correspondente conterá 107 × 107 = 1014 entradas. Isso é um número grande de entradas! E isso torna a computação H ^ − 1 ∇C extremamente difícil na prática. No entanto, isso não significa que não seja útil entender. De fato, há muitas variações na descida de gradiente que são inspiradas pela Hessian Optimization, mas que evitam o problema com matrizes excessivamente grandes. Vamos dar uma olhada em uma dessas técnicas, a descida do gradiente baseada em Momentum.
Momentum
Intuitivamente, a vantagem da Hessian Optimization é que ela incorpora não apenas informações sobre o gradiente, mas também informações sobre como o gradiente está mudando. A descida do gradiente baseada no Momentum baseia-se em uma intuição similar, mas evita grandes matrizes de derivadas secundárias. Para entender a técnica de Momentum, pense em nossa imagem original de descida do gradiente, na qual consideramos uma bola rolando em um vale (veja figura abaixo). Observamos que a descida do gradiente é, apesar de seu nome, apenas vagamente semelhante a uma bola caindo no fundo de um vale.
A técnica de Momentum modifica a descida do gradiente de duas maneiras que a tornam mais semelhante à imagem física. Primeiro, introduz uma noção de “velocidade” para os parâmetros que estamos tentando otimizar. O gradiente atua para alterar a velocidade, não (diretamente) a “posição”, da mesma maneira que as forças físicas alteram a velocidade, afetando apenas indiretamente a posição. Em segundo lugar, o método Momentum introduz um tipo de termo de fricção, que tende a reduzir gradualmente a velocidade.
Vamos dar uma descrição matemática mais precisa. Introduzimos variáveis de velocidade v = v1, v2,…, uma para cada variável wj correspondente. Então nós substituímos a regra de atualização de descida de gradiente w → w′ = w − η∇C por:
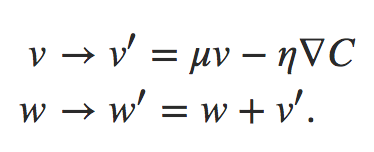
Nessas equações, μ é um hiperparâmetro que controla a quantidade de amortecimento ou atrito no sistema. Para entender o significado das equações, é útil considerar primeiro o caso onde μ = 1, o que corresponde a nenhum atrito. Quando esse é o caso, a inspeção das equações mostra que a “força” ∇C está agora modificando a velocidade, v, e a velocidade está controlando a taxa de variação de w. Intuitivamente, nós aumentamos a velocidade adicionando repetidamente termos de gradiente a ela. Isso significa que se o gradiente estiver na (aproximadamente) mesma direção através de várias rodadas de aprendizado, poderemos desenvolver um pouco de vapor movendo-se nessa direção. Pense, por exemplo, no que acontece se estivermos nos movendo diretamente por um declive:
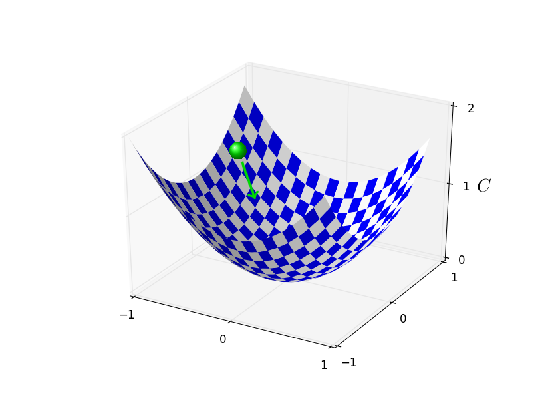
A cada passo a velocidade se torna maior no declive, então nos movemos mais e mais rapidamente para o fundo do vale. Isso pode permitir que a técnica de Momentum funcione muito mais rapidamente do que a descida de gradiente padrão. Claro, um problema é que, uma vez que chegarmos ao fundo do vale, vamos ultrapassar. Ou, se o gradiente deve mudar rapidamente, então podemos nos encontrar indo na direção errada. Essa é a razão para o hiperparâmetro µ nas equações acima.
Eu disse anteriormente que μ controla a quantidade de atrito no sistema; para ser um pouco mais preciso, você deve pensar em 1 − μ como a quantidade de atrito no sistema. Quando μ = 1, como vimos, não há atrito e a velocidade é completamente controlada pelo gradiente ∇C. Em contraste, quando μ = 0 há muito atrito, a velocidade não pode se acumular e as equações acima reduzem à equação usual para o gradiente descendente, w → w ′ = w − η∇C. Na prática, usar um valor intermediário entre 0 e 1 pode nos dar muito do benefício de ser capaz de aumentar a velocidade, mas sem causar overshooting. Podemos escolher um valor para μ usando os dados de validação retidos, da mesma maneira que selecionamos η e λ.
Evitei nomear o hiperparâmetro μ até agora. A razão é que o nome padrão para μ é mal escolhido: é chamado de coeficiente de momentum. Isso é potencialmente confuso, já que μ não é de maneira alguma a noção de momento da física. Pelo contrário, está muito mais relacionado ao atrito. No entanto, o termo coeficiente de momentum é amplamente utilizado, por isso continuaremos a usá-lo.
Uma coisa boa sobre a técnica do Momentum é que não é preciso quase nenhum trabalho para modificar uma implementação de descida de gradiente para incorporar o Momentum. Ainda podemos usar a retropropagação para calcular os gradientes, assim como antes, e usar ideias como a amostragem de mini-lotes estocasticamente escolhidos. Desta forma, podemos obter algumas das vantagens da Hessian Optimization, usando informações sobre como o gradiente está mudando, mas sem as desvantagens e com apenas pequenas modificações no nosso código. Na prática, a técnica do Momentum é comumente usada e, muitas vezes, acelera o aprendizado.
Até o próximo capítulo!
Referências:
Deep Learning Para Aplicações de IA com PyTorch e Lightning
Practical Recommendations for Gradient-Based Training of Deep Architectures
Gradient-Based Learning Applied to Document Recognition
Neural Networks & The Backpropagation Algorithm, Explained
Neural Networks and Deep Learning
The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition