Capítulo 60 – Variational Autoencoders (VAEs) – Definição, Redução de Dimensionalidade, Espaço Latente e Regularização

Nos últimos anos, modelos generativos baseados em aprendizado profundo ganharam cada vez mais interesse devido a (e implicando) algumas melhorias surpreendentes em Inteligência Artificial. Contando com uma enorme quantidade de dados, arquiteturas de rede bem projetadas e técnicas de treinamento inteligentes, os modelos generativos profundos demonstraram uma capacidade incrível de produzir peças de conteúdo altamente realistas de vários tipos, como imagens, textos e sons. Entre esses modelos, duas famílias principais se destacam e merecem uma atenção especial: Redes Adversárias Generativas (GANs) e Autoencoders Variacionais (VAEs). O primeiro já estudamos e agora estudaremos o segundo.

Em um capítulo anterior, discutimos em profundidade as Redes Adversárias Generativas (GANs) e mostramos, em particular, como o treinamento antagônico pode opor duas redes, um gerador e um discriminador, para pressionar ambas a melhorar iteração após iteração. Apresentamos agora, neste capítulo, outro tipo de modelo generativo profundo: Autoencoders Variacionais (VAEs – Variational Autoencoders).

Em resumo, um VAE é um Autoencoder cuja distribuição de codificações é regularizada durante o treinamento, a fim de garantir que seu espaço latente tenha boas propriedades, o que nos permite gerar novos dados. Além disso, o termo “variacional” vem da estreita relação que existe entre a regularização e o método de inferência variacional em Estatística.

Mas o conceito por trás dos VAEs também pode levantar muitas questões. Qual é o espaço latente e por que regularizá-lo? Como gerar novos dados a partir dos VAEs? Qual é a ligação entre VAEs e inferência variacional? Para descrever os VAEs da melhor maneira possível, tentaremos responder a todas essas perguntas (e muitas outras!) e fornecer a você o máximo de informação e conhecimento possível (variando de intuições básicas a detalhes matemáticos mais avançados). Assim, o objetivo deste capítulo não é apenas discutir as noções fundamentais dos Variational Autoencoders (VAEs), mas também construir passo a passo e começar desde o início o raciocínio que leva a essas noções (como sempre fazemos em nossos cursos na Data Science Academy). E vamos começar com o conceito de redução de dimensionalidade.

O Que é Redução de Dimensionalidade?

No aprendizado de máquina, a redução de dimensionalidade é o processo de redução do número de recursos (atributos) que descrevem alguns dados. Essa redução é feita por seleção (apenas alguns recursos existentes são conservados) ou por extração (um número reduzido de novos recursos é criado com base nos recursos antigos) e pode ser útil em muitas situações que exigem dados de baixa dimensionalidade (visualização de dados, armazenamento, computação pesada, etc…). Embora existam muitos métodos diferentes de redução de dimensionalidade, podemos definir uma estrutura global que seja compatível com a maioria desses métodos.

Primeiro, vamos codificar o processo que produz a representação de “novos recursos” a partir da representação de “recursos antigos” (por seleção ou por extração) e decodificar o processo inverso. A redução de dimensionalidade pode então ser interpretada como compactação de dados, onde o codificador compacta os dados (do espaço inicial para o espaço codificado, também chamado de espaço latente) enquanto o decodificador os descompacta. Obviamente, dependendo da distribuição inicial dos dados, da dimensão do espaço latente e da definição do codificador, essa compactação pode ser perdida, o que significa que uma parte da informação é perdida durante o processo de codificação e não pode ser recuperada durante a decodificação.

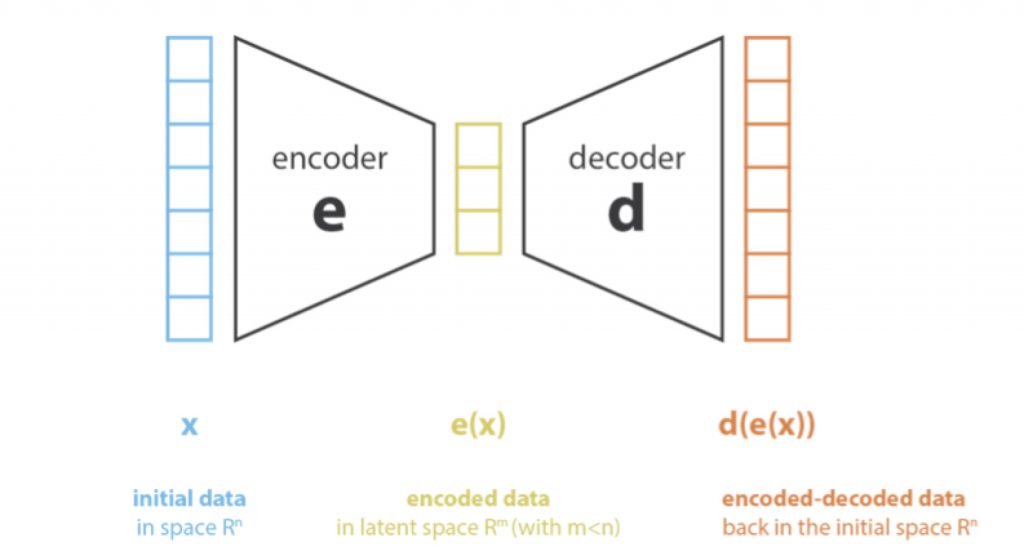
O principal objetivo de um método de redução de dimensionalidade é encontrar o melhor par codificador / decodificador entre uma determinada família. Em outras palavras, para um determinado conjunto de codificadores e decodificadores possíveis, estamos procurando o par que mantém o máximo de informações ao codificar e, portanto, tem o mínimo de erro de reconstrução ao decodificar. Se denotarmos respectivamente E e D as famílias de codificadores e decodificadores que estamos considerando, o problema da redução de dimensionalidade pode ser escrito:

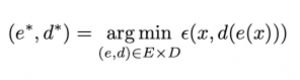
Onde:

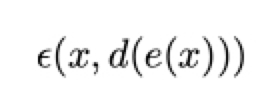
define a medida do erro de reconstrução entre os dados de entrada x e os dados codificados e decodificados d (e (x)).

Análise de Componentes Principais (PCA) e Autoencoders

Um dos primeiros métodos que vêm à mente quando se fala em redução de dimensionalidade é a análise de componentes principais (PCA). Para mostrar como ele se encaixa na estrutura que acabamos de descrever e criar o link para os Autoencoders, vamos dar uma visão geral de como o PCA funciona, deixando a maioria dos detalhes de lado (caso queira estudar o PCA em detalhes e na prática, há um capítulo inteiro dedicado a esta técnica em Matemática Para Data Science) .

A ideia do PCA é construir novos recursos independentes, que são combinações lineares dos novos recursos antigos e, de modo que as projeções dos dados no subespaço definido por esses novos recursos sejam o mais próximo possível dos dados iniciais (em termos de distância euclidiana). Em outras palavras, o PCA está procurando o melhor subespaço linear do espaço inicial (descrito por uma base ortogonal de novos recursos), de modo que o erro de aproximar os dados por suas projeções nesse subespaço seja o menor possível.

Traduzido em nossa estrutura global, procuramos um codificador na família E das matrizes n_e por n_d (transformação linear) cujas linhas são ortonormais (independência de recursos) e pelo decodificador associado entre a família D de matrizes n_d por n_e. Pode-se mostrar que os autovetores unitários correspondentes aos n_e maiores autovalores (em norma) da matriz de características de covariância são ortogonais (ou podem ser escolhidos assim) e definem o melhor subespaço da dimensão n_e para projetar dados com erro mínimo de aproximação. Assim, esses n_e autovetores podem ser escolhidos como nossos novos recursos e, portanto, o problema de redução de dimensão pode ser expresso como um problema de autovalor / autovetor. Além disso, também pode ser mostrado que, nesse caso, a matriz decodificadora é a transposta da matriz codificadora (se esses conceitos de Matemática parecem estranhos a você recomendamos Matemática Para Data Science).

Os Autoencoders são em essência, redes neurais para redução de dimensionalidade. A ideia geral dos Autoencoders é bastante simples e consiste em definir um codificador e um decodificador como redes neurais e aprender o melhor esquema de codificação-decodificação usando um processo de otimização iterativo. Assim, a cada iteração, alimentamos a arquitetura do autoencoder (o codificador seguido pelo decodificador) com alguns dados, comparamos a saída decodificada com os dados iniciais e retropropagamos o erro na arquitetura para atualizar os pesos das redes.

Assim, intuitivamente, a arquitetura geral do autoencoder (codificador + decodificador) cria um gargalo de dados que garante que apenas a parte estruturada principal da informação possa passar e ser reconstruída. Observando nossa estrutura geral, a família E dos codificadores considerados é definida pela arquitetura da rede do codificador, a família D dos decodificadores considerados é definida pela arquitetura da rede do decodificador e a busca do codificador e decodificador que minimiza o erro de reconstrução é feita por descida do gradiente sobre os parâmetros dessas redes.

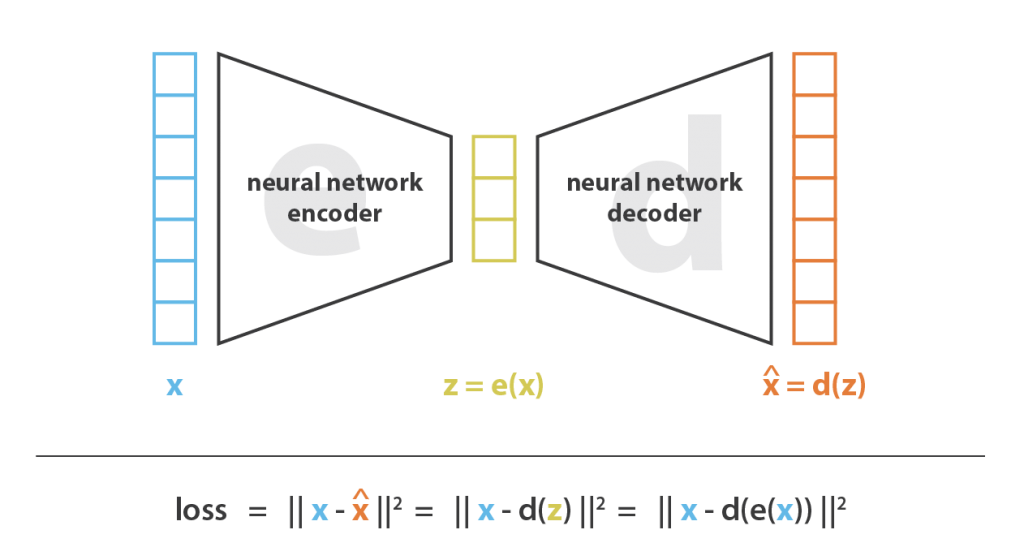
Vamos primeiro supor que nossas arquiteturas de codificador e decodificador tenham apenas uma camada sem não linearidade (autoencoder linear). Esse codificador e decodificador são transformações lineares simples que podem ser expressas como matrizes. Em tal situação, podemos ver um vínculo claro com o PCA no sentido de que, assim como o PCA, estamos procurando o melhor subespaço linear para projetar dados com o mínimo de perda de informações possível ao fazê-lo. As matrizes de codificação e decodificação obtidas com o PCA definem naturalmente uma das soluções que gostaríamos de alcançar por descida do gradiente, mas devemos destacar que essa não é a única. De fato, várias bases podem ser escolhidas para descrever o mesmo subespaço ideal e, portanto, vários pares de codificador / decodificador podem fornecer o erro de reconstrução ideal. Além disso, para autoencoders lineares e, ao contrário do PCA, os novos recursos não precisam ser independentes (sem restrições de ortogonalidade nas redes neurais).

Agora, vamos supor que o codificador e o decodificador sejam profundos e não lineares. Nesse caso, quanto mais complexa a arquitetura, mais o autoencoder pode prosseguir para uma alta redução de dimensionalidade, mantendo baixa a perda de reconstrução. Intuitivamente, se nosso codificador e nosso decodificador tiver graus de liberdade suficientes, podemos reduzir qualquer dimensionalidade inicial para 1. De fato, um codificador com “poder infinito” poderia teoricamente pegar nossos N pontos de dados iniciais e codificá-los como 1, 2, 3, … até N (ou mais geralmente, como N inteiro no eixo real) e o decodificador associado pode fazer a transformação reversa, sem perda durante o processo.

Aqui, porém, devemos ter duas coisas em mente. Primeiro, uma importante redução de dimensionalidade sem perda de reconstrução costuma ter um preço: a falta de estruturas interpretáveis e exploráveis no espaço latente (falta de regularidade). Segundo, na maioria das vezes, o objetivo final da redução da dimensionalidade não é apenas reduzir o número de dimensões dos dados, mas reduzir esse número de dimensões, mantendo a maior parte das informações da estrutura de dados nas representações reduzidas. Por essas duas razões, a dimensão do espaço latente e a “profundidade” dos autoencoders (que definem o grau e a qualidade da compressão) devem ser cuidadosamente controladas e ajustadas, dependendo do objetivo final da redução da dimensionalidade.

Variational Autoencoders (VAEs)

No capítulo 58 introduzimos o conceito de Autoencoders, que são arquiteturas de codificador-decodificador que podem ser treinadas por descida do gradiente. Vamos agora fazer o link com o problema de geração de conteúdo, ver as limitações dos Autoencoders em sua forma atual para esse problema e introduzir os Autoencoders Variacionais.

Limitações de Autoencoders para Geração de Conteúdo

Nesse ponto, uma pergunta natural que vem à mente é “qual é o link entre os Autoencoders e a geração de conteúdo?”. De fato, uma vez que o Autoencoder foi treinado, temos um codificador e um decodificador, mas ainda não há uma maneira real de produzir qualquer novo conteúdo. À primeira vista, poderíamos ficar tentados a pensar que, se o espaço latente for regular o suficiente (bem “organizado” pelo codificador durante o processo de treinamento), poderíamos pegar um ponto aleatoriamente nesse espaço latente e decodificá-lo para obter um novo conteúdo. O decodificador agiria mais ou menos como o gerador de uma Rede Adversária Generativa .

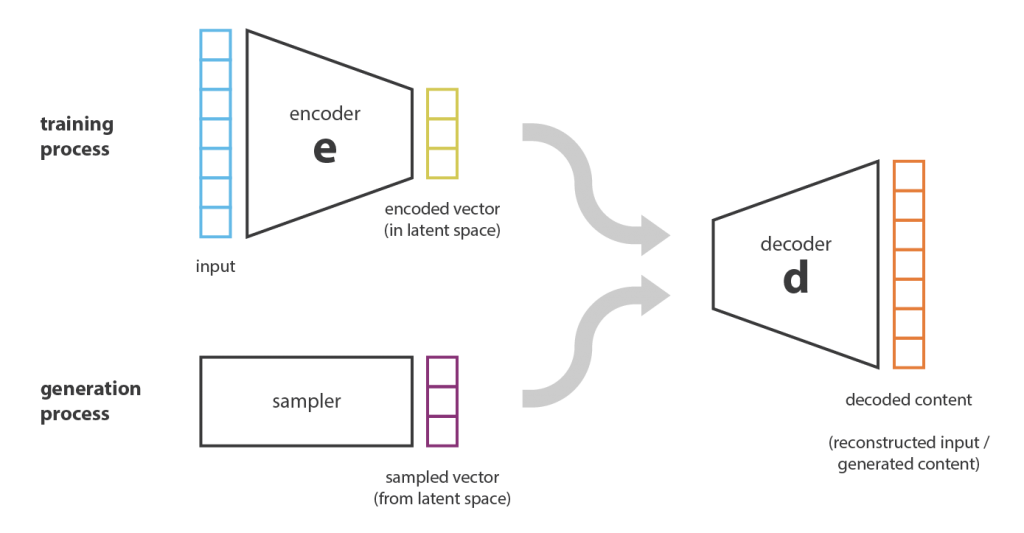
No entanto, a regularidade do espaço latente para Autoencoders é um ponto difícil que depende da distribuição dos dados no espaço inicial, da dimensão do espaço latente e da arquitetura do codificador. Portanto, é bastante difícil (se não impossível) garantir, a priori, que o codificador organize o espaço latente de maneira inteligente, compatível com o processo generativo que acabamos de descrever.

Para ilustrar esse ponto, vamos considerar o exemplo no qual descrevemos um codificador e um decodificador suficientemente poderosos para colocar N dados de treinamento inicial no eixo real (cada ponto de dados sendo codificado como um valor real) e decodificá-los sem nenhum perda de reconstrução. Nesse caso, o alto grau de liberdade do Autoencoder que possibilita a codificação e decodificação sem perda de informações (apesar da baixa dimensionalidade do espaço latente) leva a uma super adaptação severa, o que implica que alguns pontos do espaço latente fornecerão conteúdo sem sentido uma vez decodificado. Se esse exemplo unidimensional tiver sido voluntariamente escolhido para ser extremo, podemos notar que o problema da regularidade espacial latente dos Autoencoders é muito mais geral do que isso e merece uma atenção especial.

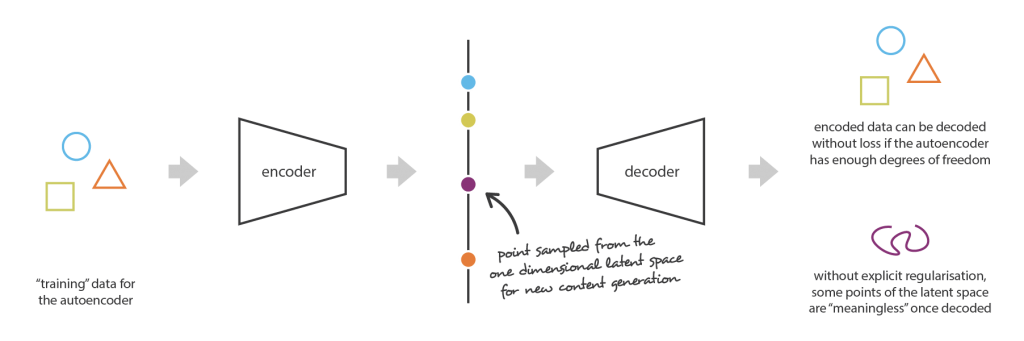
Ao pensar nisso por um minuto, essa falta de estrutura entre os dados codificados no espaço latente é bastante normal. De fato, o Autoencoder é treinado apenas para codificar e decodificar com o mínimo de perdas possível, independentemente da organização do espaço latente. Portanto, se não tomarmos cuidado com a definição da arquitetura, é natural que, durante o treinamento, a rede aproveite todas as possibilidades de sobreajuste para realizar sua tarefa da melhor forma possível … a menos que a regularizemos explicitamente!

Definição de Autoencoders Variacionais

Portanto, para poder usar o decodificador de nosso autoencoder para fins generativos, precisamos ter certeza de que o espaço latente é regular o suficiente. Uma solução possível para obter essa regularidade é introduzir regularização explícita durante o processo de treinamento. Assim, como mencionamos brevemente na introdução deste capítulo, um autoencoder variacional pode ser definido como um autoencoder cujo treinamento é regularizado para evitar sobreajuste e garantir que o espaço latente tenha boas propriedades que possibilitem processos generativos.

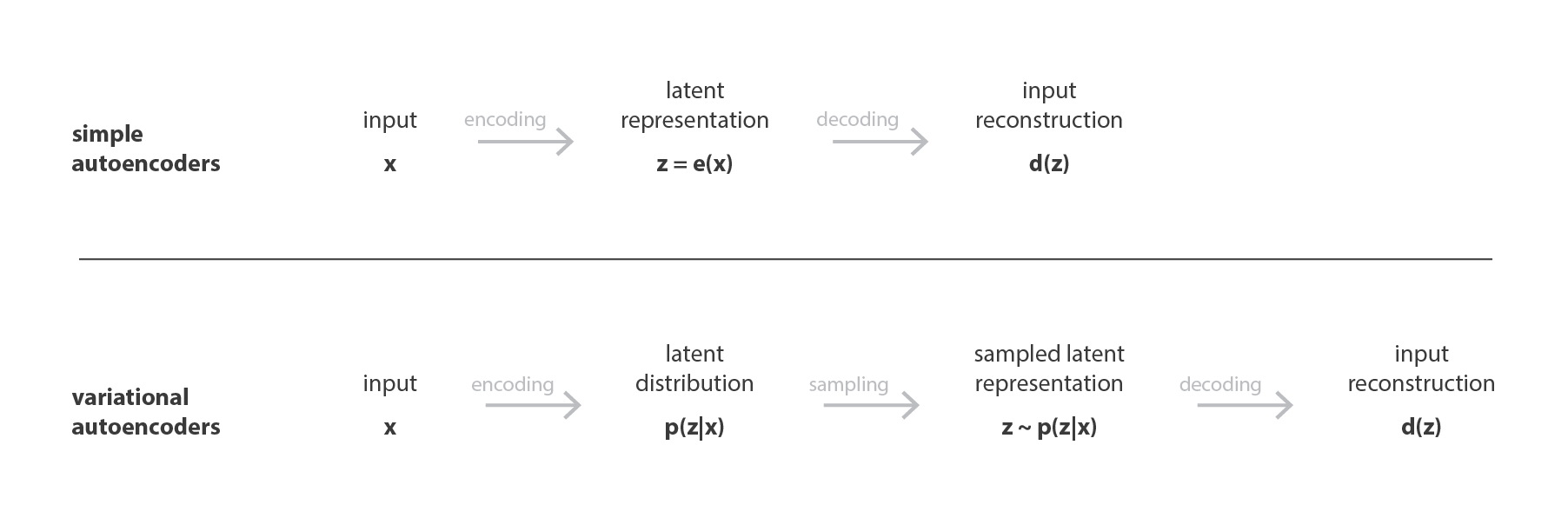
Assim como um autoencoder padrão, um autoencoder variacional é uma arquitetura composta por um codificador e um decodificador, treinada para minimizar o erro de reconstrução entre os dados decodificados e os dados iniciais. No entanto, para introduzir alguma regularização do espaço latente, procedemos a uma ligeira modificação do processo de codificação / decodificação: em vez de codificar uma entrada como um único ponto, a codificamos como uma distribuição no espaço latente. O modelo é treinado da seguinte maneira:

Primeiro, a entrada é codificada como distribuição no espaço latente.
Segundo, um ponto do espaço latente é amostrado a partir dessa distribuição.
Terceiro, o ponto amostrado é decodificado e o erro de reconstrução pode ser calculado.
Finalmente, o erro de reconstrução é retropropagado pela rede.

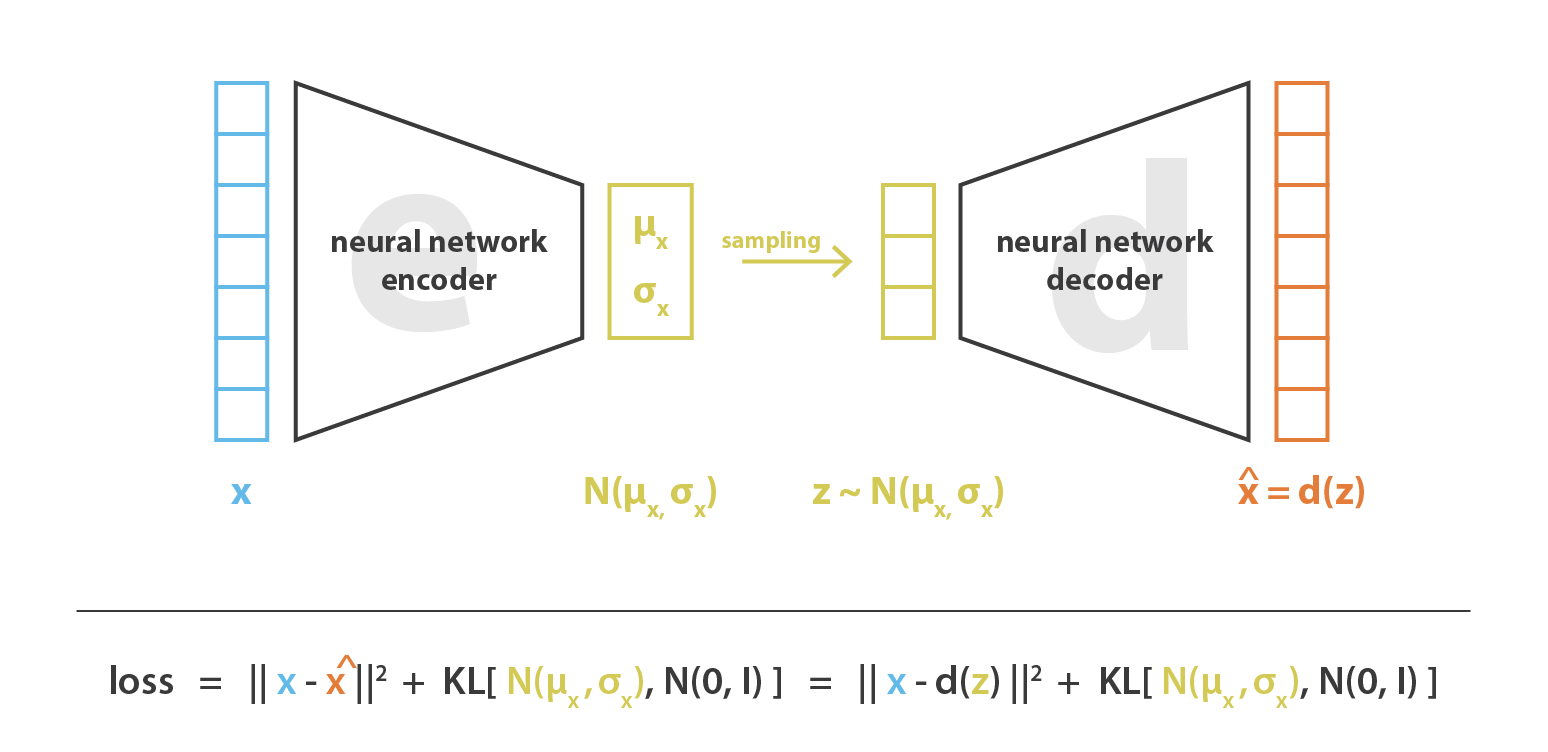
Na prática, as distribuições codificadas são escolhidas para serem normais, de modo que o codificador possa ser treinado para retornar a média e a matriz de covariância que descrevem esses gaussianos. A razão pela qual uma entrada é codificada como uma distribuição com alguma variância em vez de um único ponto é que torna possível expressar muito naturalmente a regularização do espaço latente: as distribuições retornadas pelo codificador são impostas para estarem próximas a uma distribuição normal padrão. Veremos na próxima subseção que garantimos dessa maneira uma regularização local e global do espaço latente (local por causa do controle de variância e global por causa do controle médio).

Assim, a função de perda que é minimizada ao treinar um VAE é composta de um “termo de reconstrução” (na camada final), que tende a tornar o esquema de codificação-decodificação o mais eficiente possível e um “termo de regularização” (no camada latente), que tende a regularizar a organização do espaço latente, tornando as distribuições retornadas pelo codificador próximas a uma distribuição normal padrão. Esse termo de regularização é expresso como a divergência de Kulback-Leibler entre a distribuição retornada e uma gaussiana padrão e será mais justificado na próxima seção. Podemos notar que a divergência de Kullback-Leibler entre duas distribuições gaussianas tem uma forma fechada que pode ser expressa diretamente em termos das médias e das matrizes de covariância das duas distribuições.

Intuições Sobre a Regularização

A regularidade que se espera do espaço latente para possibilitar o processo generativo pode ser expressa por meio de duas propriedades principais: continuidade (dois pontos de fechamento no espaço latente não devem fornecer dois conteúdos completamente diferentes uma vez decodificados) e integridade (para uma distribuição escolhida , um ponto amostrado no espaço latente deve fornecer conteúdo “significativo” depois de decodificado).

O único fato de que os VAEs codificam entradas como distribuições, em vez de pontos simples, não é suficiente para garantir continuidade e integridade. Sem um termo de regularização bem definido, o modelo pode aprender, a fim de minimizar seu erro de reconstrução, “ignorar” o fato de que as distribuições são retornadas e se comportam quase como os autoencoders clássicos (levando ao super ajuste). Para fazer isso, o codificador pode retornar distribuições com pequenas variações (que tendem a ser distribuições pontuais) ou retornar distribuições com meios muito diferentes (que ficariam muito distantes um do outro no espaço latente). Nos dois casos, as distribuições são usadas da maneira errada (cancelando o benefício esperado) e a continuidade e / ou a integridade não são satisfeitas.

Portanto, para evitar esses efeitos, precisamos regularizar a matriz de covariância e a média das distribuições retornadas pelo codificador. Na prática, essa regularização é feita impondo distribuições para estar perto de uma distribuição normal padrão (centralizada e reduzida). Dessa forma, exigimos que as matrizes de covariância estejam próximas da identidade, impedindo distribuições pontuais e com a média próxima de 0, impedindo que as distribuições codificadas estejam muito distantes umas das outras.

Com esse termo de regularização, impedimos que o modelo codifique dados distantes no espaço latente e incentivamos o máximo possível as distribuições retornadas a “se sobrepor”, satisfazendo dessa maneira as condições de continuidade e integridade esperadas. Naturalmente, como em qualquer termo de regularização, isso tem o preço de um erro de reconstrução mais alto nos dados de treinamento. A troca entre o erro de reconstrução e a divergência de KL pode, no entanto, ser ajustada e veremos no próximo capítulo como a expressão emerge naturalmente de nossa derivação formal.

Para concluir, podemos observar que a continuidade e a integridade obtidas com a regularização tendem a criar um “gradiente” sobre as informações codificadas no espaço latente. Por exemplo, um ponto do espaço latente que estaria a meio caminho entre as médias de duas distribuições codificadas provenientes de diferentes dados de treinamento deve ser decodificado em algo que esteja em algum lugar entre os dados que deram a primeira distribuição e os dados que deram a segunda distribuição como pode ser amostrado pelo autoencoder em ambos os casos.

Essa é uma das arquiteturas mais avançadas de Deep Learning e para uma melhor compreensão, precisamos da nossa amiga, a Matemática. No próximo capítulo traremos um pouco da Matemática por trás dos VAEs. Até lá.

Referências:

Formação Engenheiro de Inteligência Artificial

Formação Análise Estatística

Formação Cientista de Dados

Customizando Redes Neurais com Funções de Ativação Alternativas

Autoencoders – Unsupervised Learning

Understanding Variational Autoencoders (VAEs)

Deep inside: Autoencoders

Deep Learning — Different Types of Autoencoders

Contractive Auto-Encoders – Explicit Invariance During Feature Extraction

Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion

Introduction to Autoencoders